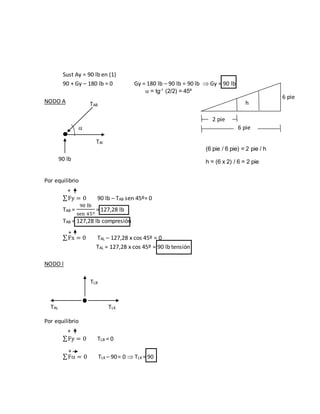
Este documento presenta el análisis estructural de una armadura Howe que soporta un techo. Se determinan las reacciones en los apoyos A y G, así como las fuerzas axiales en las barras. También se calculan los esfuerzos en las barras EF, DF y EG mediante el método de secciones.

1. REPÚBLICA BOLIVARIANA DE VENEZUELA
MINISTERIO DEL PODER POPULAR PARA LA EDUCACIÓN
UNIVERSIDAD FERMÍN TORO
CABUDARE – EDO. LARA
Análisis Estructural
(ARMADURAS)
Alumno: Brayan Briceño
C.I.: 23.833.486

2. Análisis Estructural
ARMADURAS
1.- La Armadura HOWE mostrada se utiliza para soportar un Techo. Suponga Los
Apoyos en A y G como soportes de Rodillos. a) Dibuje diagrama de cuerpo libre b)
Determine las Reacciones en los apoyos A y G, c) Determine las fuerzas Axiales en las
barras AB , BC, BL, BK
b) Reacciones en los apoyos
Ecuación de equilibrio
∑Fy = 0 Ay + Gy – 20 lb – 40 lb -60lb – 40lb – 20 lb = 0 (1)
∑Mg = 0 - Ay x 12 pie + 20 lb x 10 pie + 4 lb x 8 pie + 60 lb x 6 pie + 40 lb x 4
pie + 20 lb x 20 pie = 0 (2)
Ay x12 pie = 200 lbpie + 320 lbpie + 360 lbpie + 160Lbpie + 40 lbpie
Ay =
1080 lbpie
12 pie
= 90 lb
A
B
C
D
G
2pie 2pie 2pie2pie2pie2pie
20 lb20 lb
40 lb40 lb
60 lb
6pie
KL
Ay Gy
+
Ay
+

3. Sust Ay = 90 lb en (1)
90 + Gy – 180 lb = 0 Gy = 180 lb – 90 lb = 90 lb  Gy = 90 lb
NODO A
Por equilibrio
∑Fy = 0 90 lb – TAB sen 45º= 0
TAB =
90 lb
sen 45º
= 127,28 lb
TAB = 127,28 lb compresión
∑Fx = 0 TAL – 127,28 x cos 45º = 0
TAL = 127,28 x cos 45º = 90 lb tensión
NODO l
Por equilibrio
∑Fy = 0 TLB = 0
∑F = 0 TLK – 90= 0  TLK = 90
+

TAB
TAl
90 lb
h
6 pie
2 pie
6 pie
 = tg-1
(2/2) = 45º
(6 pie / 6 pie) = 2 pie / h
h = (6 x 2) / 6 = 2 pie
TLB
TAL TLK
+
+
+

4. NODO B
Por equilibrio
∑Fy = 0 127,28 lb x sen 45º + TBC x sen 45º - TBK x sen 45º - 20 lb = 0 (1)
∑F = 0 127,28 lb x cos 45º + TBC x cos 45º - TBK x cos 45º = 0 (2)
TAB = 127,28 lb
Sumando(1) y (2)
127,28 x sen45º + TBC x sen45º - TBK sen45º - 20 = 0
127,28 x cos 45º + TBC x cos 45º - TBK cos 45º = 0
180 + 141 TBC – 20 = 0
TBC = (-180 + 20)/1,414 = -113,15 lb
TBC = 113,15 lb compresión
SustTBC = -113,15 lb en(1)
127,28 x sen45º - 113,15 x sen45º - TBK x sen45º - 20 = 0
TBK x sen45º= -80 +90 – 20
TBK = (-10/sen45º) = -14,14lb
TBK = 14,14lb compresión
FUERZAS AXIALES
TAB = 127,28 lbcompresión
TBC = 113,15 lb compresión
TBL = 0
TBK= 14,14 lb compresión
+
+
45º
45º
45º
TAB
TBK
TBC
20 lb

5. 2).- Determine por Método de Secciones (corte) los esfuerzos a que están sometidos
las barras EF, DF, Y EG de la figura. Si DF = 4 mts. y DE = 3 mts, simétrica en su
forma. NOTA: Apoyo RB es Rodante (móvil)
REACCIÓN EN LOS APOYOS.
∑ MA = 0 -12Kn x 4 m – 20 Kn x 8 m – 8 Kn x 3 m + RBY x 12 m = 0
RBY x 12 m = 48 Kn x m + 160 Kn x m + 24 Kn x m
RBY = (232 x m /12 m) = 19,33 Kn
∑Fx = 0 - RAX + 8 Kn = 0 RAX = 8 Kn
∑Fy = 0 - RAy + 19,33 Kn – 32 Kn = 0 RAy = 32 Kn – 19,33 Kn
RAy = 12,67 Kn
RA RB
12Kn 20Kn
8Kn
E
FD
G
3 m
4 m
RAY RBY
RAX
4 m
I
I’
+
+
+

6. Aplicando Método Sección (Corte I I’)
Tomamos el lado izquierdo del corte
Ecuación de equilibrio
∑ ME = 0 19,33 Kn x 8 m – 8 Kn x 3 m – 20 Kn x 4 m + TFD x 3 m = 0
TFD x 3 m = 24 Kn x m + 80 Kn x m – 154,64 Kn x m
TFD = (54,64 Kn x m / 3m) = -16,88 Kn
TFD = 16,88 Kn (compresión)
∑Fy = 0 -20 Kn + 19,33 Kn - TFE x sen 45º
TFE = (-0,67 x Kn / sen 45º) = -0,95 Kn
TFE = 0,95 Kn (compresión)
∑Fx = 0 -8 Kn – TFD – TGE – TFE xcos 45º = 0
TGE = 8 Kn –(-16,88) – (-0,95) cos 45º
TGE = 25,55 Kn (tracción)
19,33
TEE
TFE
TFD
E
8 m
3m
+
+
+