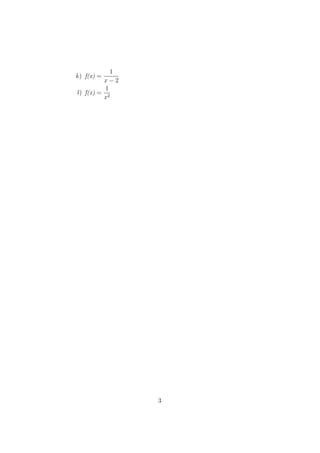Este documento presenta una serie de ejercicios relacionados con funciones. Incluye preguntas sobre si ciertas relaciones son funciones, cálculos de imágenes e preimágenes de funciones definidas, determinación de dominios máximos de funciones reales, y análisis de gráficas funcionales.

1. Ejercicios de clase
1. Sea A={1, 2, 3, 4} y B={a, b, c, d}. Para cada una de las relaciones siguientes, justifique si es una funci´n:
o
a) {(1, a), (2, a), (3, c), (4, b)}
b) {(1, b), (2, b), (3, c), (3, d), (4, c)}
c) {(1, b), (2, b), (3, b), (4, b)}
d ) {(1, a), (2, d), (3, c), (4, b)}
e) {(1, b), (2, b), (4, b)}
2. En cada caso, determine la imagen de los n´meros indicados.
u
√
a) f(x) = x + 1, halle f(0), f(1), f(-1).
b) f(x) = 3x3 − x, halle f (5), f (4) y f (-2).
√
3x
c) f(x) = 2
, halle f (0), f (1), f ( 2), f (-1).
x +1
1
d ) f(x) = −3 + 2x, halle f (-3), f (-5) y f ( 2 )
e) f(x) = x3 − x + 1, halle f (2), f (-3) y f (0).
x−1
, halle f (7) y f (-5).
f ) f(x) =
x
3. Calcule las preim´genes que se le solicitan:
a
x+3
, calcule la preim´gen de 0, 2 y -1.
a
x−6
√
b) h(x) = x − 8, halle la preim´gen de 0, 16 y -4.
a
a) h(x) =
c) h(x) = −2x2 + 1, calcule la preim´gen de 9, -3 y 1.
a
x2 − 4
, halle la preim´gen de -3, 0, 2 y -1.
a
x−3
√
e) h(x) = x − 1, calcule la preim´gen de 0, -2, 5 y -1.
a
d ) h(x) =
4. Calcule el dominio m´ximo de cada una de las siguientes funciones
a
reales:
√
a) f(x) = 4x + 4
x3 + 5x2 − 1
√
5
x2 − 8x
c) h(x) = −5x2 + x + 1
b) g(x) =
1

2. d ) m(x) = √
e)
f)
g)
h)
1
x2
+1
x+4
f(x) = 2
x − 3x + 2
√
3−x
g(x) = 2
4x − 21x + 5
√
3
2x5 + 1
h(x) =
x2 + 7
√
m(x) = x2 − x + 1
x+3
x+1
2
f(x) = x − 4
2x
g(x) =
x+1
√
√
g(x) = x + x + 6
√
h(x) = 5x2 + 10
i ) f(x) =
j)
k)
l)
m)
n) h(x) =
x(x + 6)
7+x
n) m(x) = √
˜
7
x − 13
1
o) m(x) = √
2x + 14
5. Analice las gr´ficas de las siguientes funciones, determine ambito, doa
´
minio m´ximo, im´genes y preim´genes solicitadas.
a
a
a
a) f(x) = 2x − 5
b) f(x) = 3x − 1
c) f(x) = 2
d ) f(x) = 2 +
√
x
e) f(x) = −3x + 6
f ) f(x) = x2 + 3
g) f(x) = x3
h) f(x) = |x + 2|
1
i ) f(x) =
x
√
j ) f(x) = 3 x
2

3. 1
x−2
1
l ) f(x) = 2
x
k ) f(x) =
3