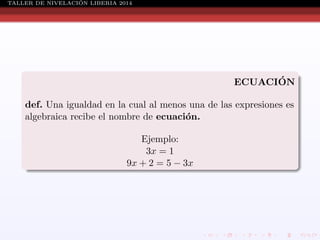
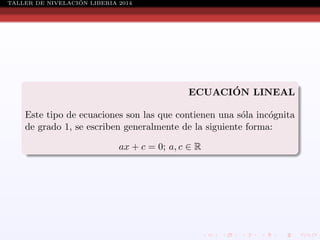
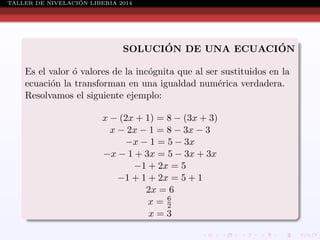
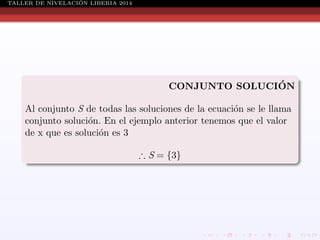
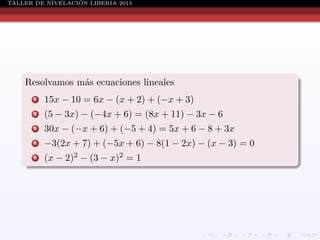
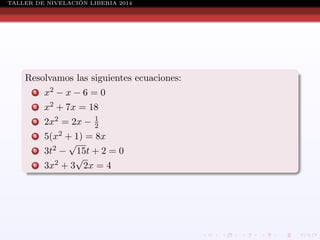
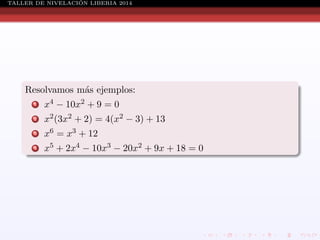
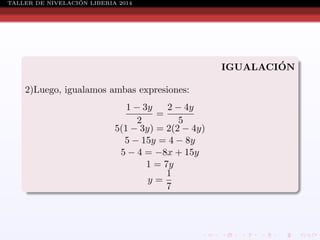
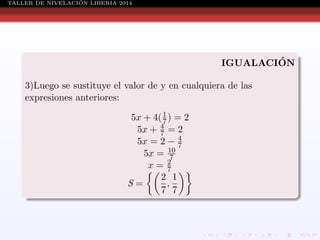
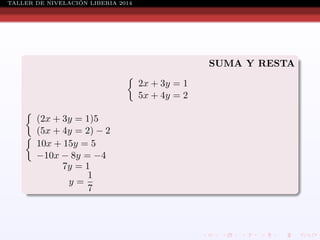
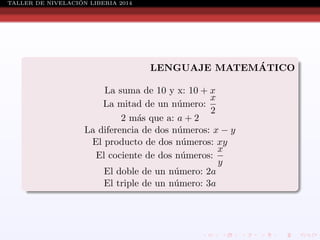
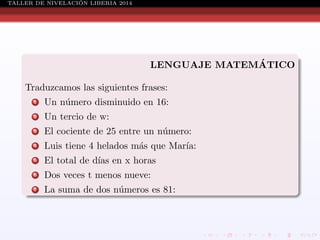
Este documento presenta información sobre ecuaciones de diferentes tipos como lineales, cuadráticas, racionales y sistemas de ecuaciones. Explica conceptos como definición de ecuación, solución de ecuaciones, conjunto solución, métodos para resolver ecuaciones cuadráticas, racionales y sistemas de ecuaciones. También incluye ejemplos resueltos de cada tipo de ecuación.