Este documento presenta las respuestas a varias preguntas sobre un dígrafo y un grafo. Para el dígrafo, se encuentra la matriz de conexión, se determina si es simple, se encuentran una cadena no simple no elemental de grado 5 y un ciclo simple, y se demuestra si es fuertemente conexo. Para el grafo, se encuentran la matriz de adyacencia y de incidencia, se determina si es conexo, simple, regular y completo, y se encuentran una cadena simple no elemental de grado 6 y un ciclo no simple de grado 5.

1. Universidad Fermín Toro
Departamento de Formación General
Escuela de Computación
Digrafo
Nombre: Joiver Sierra
Asignatura: Estructura Discreta ll
Seccion: SAIA

2. Respuestas:
1- Dado el siguiente dígrafo
a) Encontrar matriz de conexión
b) Es simple? Justifique su respuesta
c) Encontrar una cadena no simple no elemental de grado 5
d) Encontrar un ciclo simple
e) Demostrar si es fuertemente conexo utilizando la matriz de accesibilidad
f) Encontrar la distancia de v2 a los demás vértices utilizando el algoritmo de Dijkstra
a) Encontrar matriz de conexión
A1 A2 A3 A4 A5 A6 A7 A8 A9 A10 A11 A12 A13 A14
V1 0 0 0 0 0 0 0 0 1 0 0 0 0 0
V2 1 0 0 0 0 0 0 0 0 1 0 0 0 0
V3 0 1 0 0 1 0 0 0 0 0 0 0 0 0
V4 0 0 1 0 0 0 0 1 0 0 1 0 0 0
V5 0 0 0 0 0 1 1 0 0 0 0 0 0 1
V6 0 0 0 1 0 0 0 0 0 0 0 1 1 0

3. b) Es simple? Justifique su respuesta
El dígrafo si es simple, porque no tiene ningún lazo y tampoco existen arcos
paralelos que puedan partir de un mismo vértice a otro.
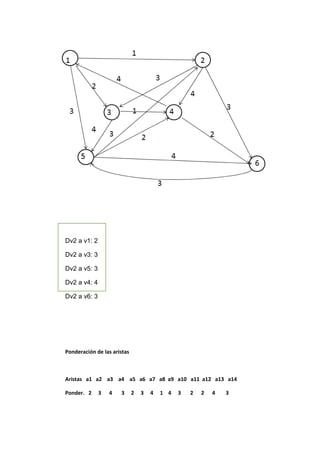
c) Encontrar una cadena no simple no elemental de grado 5
v1
v4
a6 a11 a12
a13
v5 v6
a14
C= [v1 a6 v5 a11 v4 a12 v6 a14 v5 a13 v6]
d) Encontrar un ciclo simple
V4
A11 a12
V5
A14
C=[ v5 a11 v4 a12 v6 a14 v5 ]
e) Demostrar si es fuertemente conexo utilizando la matriz de accesibilidad

4. V1 V2 V3 V4 V5 V6
V1 0 1 1 0 1 0
V2 0 0 1 1 0 1
V3 0 0 0 1 1 0
V4 1 0 0 0 0 1
V5 0 1 0 1 0 1
V6 0 0 0 0 1 0
Ma(D)=

5. V1 V2 V3 V4 V5 V6
V1 0 0 1 1 1 1
V2 1 0 0 1 1 1
V3 1 1 0 1 0 1
V4 0 1 1 0 1 0
V5 1 0 1 1 1 1
V6 0 1 0 1 0 1
M ² (D)=
V1 V2 V3 V4 V5 V6
V1 1 1 1 1 1 1
V2 1 1 1 1 1 1
V3 1 1 1 0 1 1
V4 0 1 1 1 1 1
V5 0 1 1 1 1 1
V6 1 0 1 1 0 1

6. M ³ (D)=
V1 V2 V3 V4 V5 V6
V1 1 1 1 1 1 1
V2 1 0 1 1 1 1
V3 0 1 1 1 1 1
V4 1 1 0 1 1 1
V5 1 1 1 1 1 1
V6 1 1 1 1 0 1
M ⁴ (D)=
V1 V2 V3 V4 V5 V6
V1 1 1 1 1 1 1

7. V2 1 1 1 1 1 1
V3 1 1 1 1 1 1
V4 1 1 1 1 1 1
V5 1 1 1 1 1 1
V6 1 1 1 1 0 1
M ⁵ (D)=
V1 V2 V3 V4 V5 V6
V1 3 4 5 4 5 4
V2 4 2 5 5 5 5
V3 3 4 3 4 4 4
V4 4 4 3 5 4 4
V5 3 4 4 5 4 5
V6 3 3 3 4 1 4
Acc (D)= Bin

8. • Componentes iguales a cero (0) permanecerá como cero (0)
• Componentes diferentes de cero (0) se convertirá en uno (1)
V1 V2 V3 V4 V5 V6
V1 1 1 1 1 1 1
V2 1 1 1 1 1 1
V3 1 1 1 1 1 1
V4 1 1 1 1 1 1
V5 1 1 1 1 1 1
V6 1 1 1 1 1 1
Acc (D)= Bin
Dígrafo Fuertemente Conexo
f) La distancia de v2 a los demás vértices utilizando el algoritmo de Dijkstra

9. Dv2 a v1: 2
Dv2 a v3: 3
Dv2 a v5: 3
Dv2 a v4: 4
Dv2 a v6: 3
Ponderación de las aristas
Aristas a1 a2 a3 a4 a5 a6 a7 a8 a9 a10 a11 a12 a13 a14
Ponder. 2 3 4 3 2 3 4 1 4 3 2 2 4 3

10. 1- Dado el siguiente grafo, encontrar:
a)Matriz de Adyacencia
b) Matriz de incidencia
c) Es conexo?. Justifique su respuesta
d) Es simple?. Justifique su respuesta
e) Es regular?. Justifique su respuesta
f) Es completo? Justifique su respuesta
g) Una cadena simple no elemental de grado 6
h) Un ciclo no simple de grado 5
i) Árbol generador aplicando el algoritmo constructor
j) Subgrafo parcial
k) Demostrar si es euleriano aplicando el algoritmo de Fleury
l) Demostrar si es hamiltoniano
a) Matriz de adyacencia:

11. V1 V2 V3 V4 V5 V6 V7 V8
V1 0 1 1 1 0 0 1 1
V2 1 0 1 0 1 1 0 1
V3 1 1 0 1 1 1 1 0
V4 1 0 1 0 1 0 1 0
V5 0 1 1 1 0 1 1 1
V6 0 1 1 0 1 0 0 1
V7 1 0 1 1 1 0 0 1
V8 1 1 0 0 1 1 1 0
b) Matriz de incidencia:
A1 A2 A3 A4 A5 A6 A7 A8 A9 A10 A11 A12 A13 A14 A15 A16 A17 A18 A19 A20
V1 1 1 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0
V2 1 0 1 0 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0
V3 0 1 1 0 0 0 1 0 0 0 1 1 1 0 0 0 0 0 0 0
V4 0 0 0 1 0 0 0 0 0 0 1 0 0 1 1 0 0 0 0 0
V5 0 0 0 0 0 0 0 1 0 0 0 0 1 1 0 1 1 0 1 0
V6 0 0 0 0 0 0 1 0 0 1 0 0 0 0 0 1 0 0 0 1
V7 0 0 0 0 1 0 0 0 0 0 0 1 0 0 1 0 1 1 0 0
V8 0 0 0 0 0 1 0 0 1 0 0 0 0 0 0 0 0 1 1 1
c) Es conexo? Justifique su respuesta.
El grafo es conexo porque todos los vértices se encuentran conectados con aristas
d) Es simple? Justifique su respuesta
Ma(G)
=
Mi(
G)=

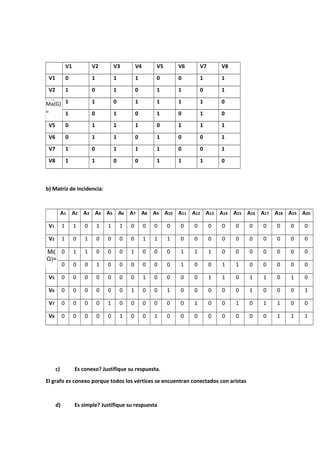
12. El grafo es simple ya que no contiene lazos ni aristas paralelas
e) Es regular? Justifique su respuesta
El grafo no es regular porque sus vértices no tienen el mismo grado
f) Es completo?. Justifique su respuesta.
El grafo no es completo porque existen pares de vértices entre los cuales no hay aristas.
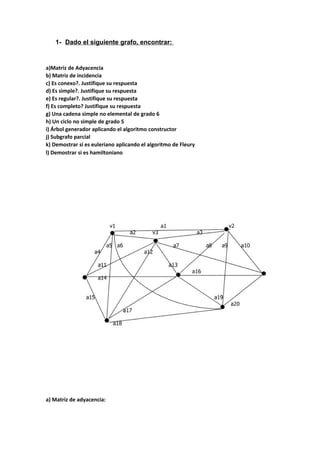
g) Una cadena simple no elemental de grado 6
C=[V1,a1,v2,a8,v5,a13,v3,a12,v7,a18,v8,a9,v2]
h) Un ciclo no simple de grado 5
C[v2,a10,v6,a20,v8,a19,v5,a16,v6,a10,v2]
i) Árbol generador aplicando el algoritmo constructor.
1ero: Usamos el vértice V1 entonces H1= {V1}
2do: agarramos la arista A1 entonces H2= {V1,V2}
3ero: seleccionamos la arista A3 entonces H3={V1,V2,V3}
V1 V2
A1
V1 V2
A1
V3
A3

13. 4to: seleccionamos la arista A11 entonces H4={V1,V2,V3,V4}
5to: Seguido tomamos la arista A14 entonces H5={V1,V2,V3,V4,V5}
6to: seleccionamos la arista A16 entonces H6={V1,V2,V3,V4,V5,V6}
V1
A1
V3
V2
V4
A3
A11
V1
A1
V2
V4
A3
A11
V3
V5
A14
V1
A1
V2
A3
A11
V3

14. 7mo: ahora la arista A20, H7={V1,V2,V3,V4,V5,V6,V8}
8vo: luego la arista A20 entonces H7={V1,V2,V3,V4,V5,V6,V8,V7}
V4
V5
A14
V6
A16
V1
A1
V2
V4
A3
A11
V3
V5
A14
V6
A16
V8
V1
A1
V2
V4
A3
A11
V3
V5
A14
V6
A16
V8V7
A20
A20
A18

15. j) Subgrafo parcial
k) Demostrar si es Euleriano aplicando el algoritmo de Fleury
El Grafo no es Eureliano ya que Aplicando el Algoritmo de Fleury se concluye que el grafo
posee aristas repetidas en el recorrido
l) Demostrar si es hamiltoniano
V1 v2
A2
A3
A14 v3 a10
V4 v5 v6
A15 a17 a19 a20
V1
V3
V2
V4 V5 V6
V7
V8
A3A2
A15
A17
A19
A20

16. V7 v8
Es Hamiltoniano ya que el número de vértices de G en 8, Gr (v1) ≥ 8/2=4
(i=1,2,8)