El documento presenta: 1) Dos matrices que representan un grafo - una matriz de adyacencia y una matriz de incidencia. 2) Se demuestra que el grafo es conexo, simple, regular y completo. 3) Se muestra un camino simple de grado 6 y un ciclo simple de grado 5 en el grafo.

1. a. MATRIZ DE ADYACENCIA DEL GRAFO:
V1 V2 V3 V4 V5 V6 V7 V8
V1 0 1 1 0 0 0 1 0
V2 1 0 1 1 1 0 0 1
V3 1 1 0 1 0 1 1 1
V4 0 1 1 0 1 0 0 1
V5 0 1 0 1 0 1 0 1
V6 1 0 1 0 1 0 1 1
V7 1 0 1 0 0 1 0 1
V8 0 1 1 1 1 1 1 0
b. MATRIZ DE INCIDENCIA DEL GRAFO:
V1 V2 V3 V4 V5 V6 V7 V8
a 1 1 1 0 0 0 0 0 0
a 2 1 0 1 0 0 0 0 0
a 3 0 0 1 0 0 0 0 0
a 4 1 0 0 0 0 0 1 0
a 5 1 0 0 0 0 0 0 0
a 6 1 0 1 0 1 0 0 0
a 7 0 1 1 1 0 0 0 0
a 8 0 1 0 0 0 0 0 1
a 9 0 1 0 0 1 0 0 0
a 10 0 0 0 1 0 0 0 0
a 11 0 0 0 0 0 0 1 0
a 12 0 0 1 0 0 1 0 0
a 13 0 0 1 0 0 0 0 1
a 14 0 0 0 0 0 1 1 1
a 15 0 0 0 0 0 1 1 0
a 16 0 0 0 1 0 0 0 1
a 17 0 0 0 0 0 1 0 0
a 18 0 0 0 0 1 1 0 1
a 19 0 0 0 0 1 0 0 1
a 20 0 0 0 1 1 0 0 0
c. Conexo? Si es conexo ya que todos sus vértices están conectados entre si.
d. Es simple? Si ya que no contiene lazos entre cada par de vértices distintos no hay mas de
una arista.
e. Es regular? Si ya que es un grafo simple
f. Completo? Si ya que es un grafo simple y tienen exactamente una arista entre cada par de
vértices.
g. Cadena simple no elemental de grado 6? Es una cadena simple y elemental de grado 6
h. Un ciclo no simple de gado 5? Es un ciclo simple ya que no repite arista y es de grado 6

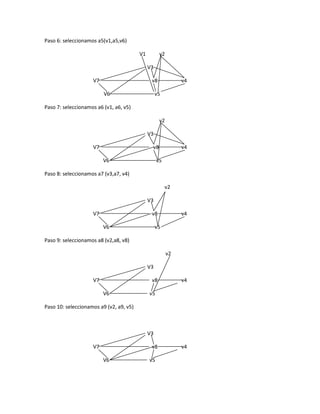
2. i. Árbol generador aplicando el algoritmo constructor
Paso 1: seleccionamos v1, h1= {v1}
a 1
Paso 2: selecciono arista (a1) v1 v2
Y h2= {v1, v3}
a 1
V1 v2
a 3
Paso 3: seleccionamos arista a3
h4= {v1, v2, v3, v4}
a 1
V1 v2
a 3
j. Sub grafo parcial:
G2=[v2,a1, g2]
V2 Cv
A2 ca
v1 a2 v2
a3
v7 v3 v4
a15 a13 a20
v6 a18 v5

3. k. Demostrar si es euleriano aplicando algoritmo de fleury
Paso 1:
Seleccionamos v1
Paso 2:
Seleccionamos a1 (v1,a1,v2)
V1 v2
V3
V7 v8 v4
V6 v5
Paso 3: seleccionamos a3 (v2, a3v3)
V1 v2
V3
V7 v8 v4
V6 v5
Paso 4: seleccionamos a2(v3,a2,v1)
V1 v2
V3
V7 v8 v4
V6 v5
Paso 5: seleccionamos a4 (v1,a4,v7)
V1 v2
V3
V7 v8 v4
V6 v5

4. Paso 6: seleccionamos a5(v1,a5,v6)
V1 v2
V3
V7 v8 v4
V6 v5
Paso 7: seleccionamos a6 (v1, a6, v5)
v2
V3
V7 v8 v4
V6 v5
Paso 8: seleccionamos a7 (v3,a7, v4)
v2
V3
V7 v8 v4
V6 v5
Paso 9: seleccionamos a8 (v2,a8, v8)
v2
V3
V7 v8 v4
V6 v5
Paso 10: seleccionamos a9 (v2, a9, v5)
V3
V7 v8 v4
V6 v5

5. Paso 11: seleccionamos a11 (v3,a11,v7)
V3
V7 v8 v4
V6 v5
Paso 12: seleccionamos a12 (v3, a12, v6)
V3
V7 v8 v4
V6 v5
Paso 13: seleccionamos a13 (v3, a13, v8)
V7 v8 v4
V6 v5
Paso 14: seleccionamos a14 ()v7,a14,v8
V7 v8 v4
V6 v5
Paso15: seleccionamos a15 (v7, a15, v6)
v8 v4
V6 v5
Paso 16: seleccionamos a16 (v4, a16, v8)
v8 v4
V6 v5

6. Paso 17: seleccionamos a17 (v6, a17, v8)
v8 v4
V6 v5
Paso 18: seleccionamos a18 (v6, a18, v5)
v8 v4
v5
Paso 19: seleccionamos a19 (v5, a19 ,v2)
v4
v5
EJERCICIO N2
A.
V1 V2 V3 V4 V5 V6
V1 0 1 1 0 1 0
V2 0 0 1 1 0 1
V3 0 0 0 1 1 0
V4 1 0 0 0 0 1
V5 0 1 0 1 0 1
V6 0 0 0 0 1 0
B. Es simple: si ya que el dígrafo no hay lazos ni arcos paralelos.
c. Cadena no simple no elemental de grado 5?
No hay cadena no simple ya que no repite aristas y es elemental por que no repite vértices.
D. Ciclo simple? a 1
V1 V2
a 9 a 3
V

7. E. demostrar si es fuerte conexo usando la matriz de accesibilidad
MATRIZ CONEXIÓN DEL DIGRAFO ES :
V1 V2 V3 V4 V5 V6
V1 0 1 1 0 1 0
V2 0 0 1 1 0 1
V3 0 0 0 1 1 0
V4 1 0 0 0 0 1
V5 0 1 0 1 0 1
V6 0 0 0 0 1 0
LA MATRIZ DE CONEXIÓN M DEL DIGRAFO SIMPLE ASOCIADO ES:
V1 V2 V3 V4 V5 V6
V1 0 1 1 0 1 0
V2 0 1 1 1 0 1
V3 0 0 0 1 1 0
V4 1 0 0 0 0 1
V5 0 1 0 1 0 1
V6 0 0 0 0 1 0
MATRIZ DE ACCESIBILIDAD:
ACC (DC) =BIN *IN+M+M2+……..M N-1]
ACC (DC) =BIN [I6+M+M2+M3+M4+M5]
MATRIZ IDENTIDAD:
F= + M
V1 V2 V3 V4 V5 V6
V1 1 0 0 0 0 0
V2 0 1 0 0 0 0
V3 0 0 1 0 0 0
V4 0 0 0 1 0 0
V5 0 0 0 0 1 0
V6 0 0 0 0 0 1
V1 V2 V3 V4 V5 V6
V1 0 1 1 0 0 0
V2 0 1 1 1 1 1
V3 0 0 0 1 0 0
V4 1 0 0 0 1 1
V5 0 1 0 1 1 1
V6 0 0 0 0 0 0

8. M2=
M3=
M4=
M5=
M6=
V1 V2 V3 V4 V5 V6
V1 1 1 1 0 0 0
V2 0 1 1 1 1 1
V3 0 0 1 1 1 0
V4 1 0 0 1 0 1
V5 0 1 0 1 2 1
V6 0 0 0 0 0 1
V1 V2 V3 V4 V5 V6
V1 2 0 1 0 0 0
V2 1 2 1 1 1 1
V3 1 0 2 1 1 0
V4 0 0 0 2 0 1
V5 0 1 0 1 3 1
V6 0 0 0 0 0 2
V1 V2 V3 V4 V5 V6
V1 3 0 1 0 0 0
V2 1 3 1 1 1 1
V3 1 0 3 1 1 0
V4 0 0 0 3 0 1
V5 0 1 0 1 4 1
V6 0 0 0 0 0 3
V1 V2 V3 V4 V5 V6
V1 4 0 1 0 0 0
V2 1 4 1 1 1 1
V3 1 0 4 1 1 0
V4 0 0 0 4 0 1
V5 0 1 0 1 5 1
V6 0 0 0 0 0 4
V1 V2 V3 V4 V5 V6
V1 5 0 1 0 0 0
V2 1 5 1 1 1 1
V3 1 0 5 1 1 0
V4 0 0 0 5 0 1
V5 0 1 0 1 6 1
V6 0 0 0 0 0 5

9. ACC (DC) =BIN [I6+M+M2+M3+M4+M5+M6]=
ACC (DC) =BIN
=
V1 ------V2
V2-------V3
V2-------V4
V2-------V5
V2-------V6
CAMINOS DE V1 A V6
V1, a1,v2=
ponderación = 2
V2,a2,v3
Ponderación =3
V2, a3,v4
Ponderación= 4
V1 V2 V3 V4 V5 V6
V1 16 2 4 0 0 0
V2 4 16 6 6 6 6
V3 4 0 15 6 5 0
V4 2 0 0 15 1 6
V5 0 6 0 6 22 6
V6 0 0 0 0 0 16
V1 V2 V3 V4 V5 V6
V1 1 1 1 0 0 0
V2 1 1 1 1 1 1
V3 1 0 1 1 1 0
V4 1 0 0 1 1 1
V5 0 1 0 1 1 1
V6 0 0 0 0 0 1

10. V2,a3,v4,a8,v3,a7,v5
Ponderación =3+1+4=8
V2,a4,v6
Ponderación =3

11. GRAFOS Y DIGRAFOS
AUTORA:
ULIMAR RIVERO
CI 19.953.263
CABUDARE 07-06-2013
UNIVERSIDAD FERMIN TORO
VICE – RECTORADO
ACADEMICO
DECANATO DE INGENIERIA
CABUDARE – LARA
ESTRUCTURA DISCRETAS II
E