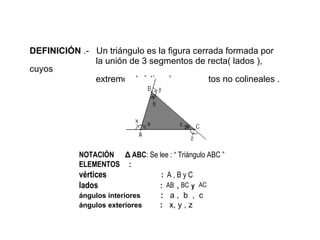
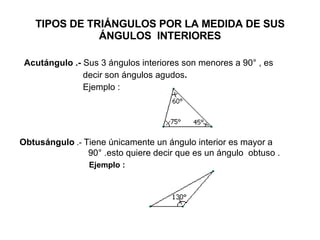
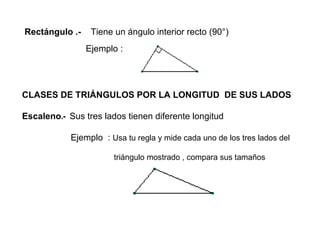
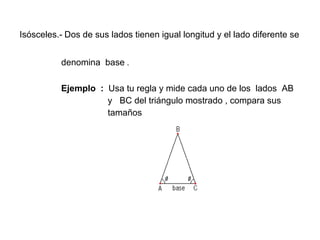
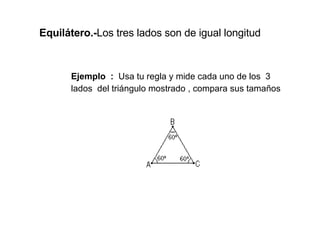
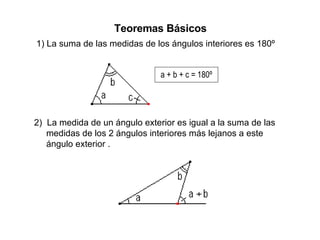
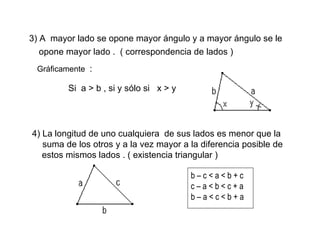
Este documento define los triángulos como figuras formadas por tres segmentos de línea unidos en tres vértices no colineales. Describe los diferentes tipos de triángulos basados en la medida de sus ángulos interiores (agudo, obtusángulo y rectángulo) y la longitud de sus lados (escaleno, isósceles y equilátero). También presenta cuatro teoremas básicos sobre la suma de los ángulos interiores, la correspondencia entre ángulos y lados opuestos, y las relaciones entre la longitud de los l

1. Raúl Ponce Yalico Universidad Nacional de Educación 20enmathe.blogspot.com

2. DEFINICIÓN .- Un triángulo es la figura cerrada formada por la unión de 3 segmentos de recta( lados ), cuyos extremos (vértices) son puntos no colineales . NOTACIÓN ∆ ABC : Se lee : “ Triángulo ABC ” ELEMENTOS : vértices : A , B y C lados : , y ángulos interiores : a , b , c ángulos exteriores : x, y , z

3. TIPOS DE TRIÁNGULOS POR LA MEDIDA DE SUS ÁNGULOS INTERIORES Acutángulo .- Sus 3 ángulos interiores son menores a 90° , es decir son ángulos agudos . Ejemplo : Obtusángulo .- Tiene únicamente un ángulo interior es mayor a 90° .esto quiere decir que es un ángulo obtuso . Ejemplo :

4. Rectángulo .- Tiene un ángulo interior recto (90°) Ejemplo : CLASES DE TRIÁNGULOS POR LA LONGITUD DE SUS LADOS Escaleno .- Sus tres lados tienen diferente longitud Ejemplo : Usa tu regla y mide cada uno de los tres lados del triángulo mostrado , compara sus tamaños

5. Isósceles.- Dos de sus lados tienen igual longitud y el lado diferente se denomina base . Ejemplo : Usa tu regla y mide cada uno de los lados AB y BC del triángulo mostrado , compara sus tamaños

6. Equilátero.- Los tres lados son de igual longitud Ejemplo : Usa tu regla y mide cada uno de los 3 lados del triángulo mostrado , compara sus tamaños

7. Teoremas Básicos 1) La suma de las medidas de los ángulos interiores es 180º a + b + c = 180º 2) La medida de un ángulo exterior es igual a la suma de las medidas de los 2 ángulos interiores más lejanos a este ángulo exterior .

8. 3) A mayor lado se opone mayor ángulo y a mayor ángulo se le opone mayor lado . ( correspondencia de lados ) Gráficamente : Si a > b , si y sólo si x > y 4) La longitud de uno cualquiera de sus lados es menor que la suma de los otros y a la vez mayor a la diferencia posible de estos mismos lados . ( existencia triangular ) b – c < a < b + c c – a < b < c + a b – a < c < b + a