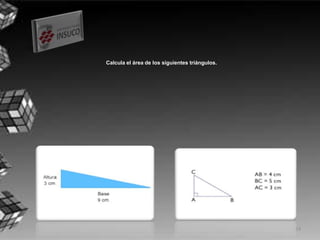
Este documento describe los diferentes tipos de triángulos basados en la longitud de sus lados, incluyendo triángulos equiláteros, isósceles y escalenos. También cubre los ángulos de los triángulos agudos, obtusos y rectos, y explica los teoremas de los ángulos internos y externos de un triángulo. Además, presenta el Teorema de Pitágoras y cómo calcular el perímetro y área de triángulos. Al final, proporciona ejercicios para aplicar estos conceptos

4. Atendiendo a sus lados los triángulos se clasifican en los siguientes tipos:
Es aquel que tiene sus tres lados de igual longitud.
Es aquel que tiene al menos dos de sus lados de igual longitud.
Tiene sus tres lados de diferente longitud .

5. Tiene un ángulo de 90 .

6. 6
Es aquel cuyo tres ángulos son agudos los ángulos de estos triángulos miden menos de 90 .
Los ángulos A,B y C de la figura miden menos de 90

7. Es el que tiene un ángulo obtuso miden mayor de 90 y menor de 180 .
El ángulo de la figura es obtuso
II
c
A
B

8. El perímetro de un triángulo es igual a las sumas de sus tres lados.

9. El área del triángulo es :
Ejemplo:

10. Teorema para ángulos internos de un triángulo: Los ángulos internos de todo triángulo suman 180 .

11. Teorema para ángulos externos de un triángulo: Un ángulo externo de un triángulo es igual a la suma de los
ángulos internos no adyacentes, es igual a 360 .

12. Denominado así porque su primera demostración formal se atribuye al filósofo griego Pitágoras.
Este teorema establece la relación entre la longitud de la hipotenusa y la de los catetos de un triángulo rectángulo.
De acuerdo con este teorema “el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos.
Su formula es:
Ejemplo:

13. Ejercicios para resolver
13
Calcula e l perímetro de cada triángulo.

14. Calcula el área de los siguientes triángulos.
14

15. Suma los ángulos internos de cada triángulo.
15

16. Suma los ángulos externos de los siguientes triángulos.
16

17. Resuelve los siguientes triángulos con el procedimiento que indica el Teorema de Pitágoras.
17