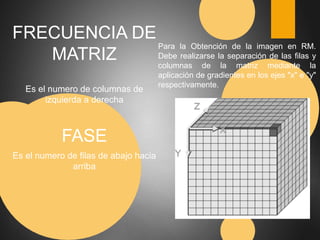
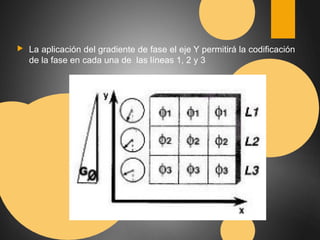
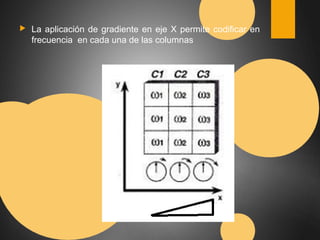
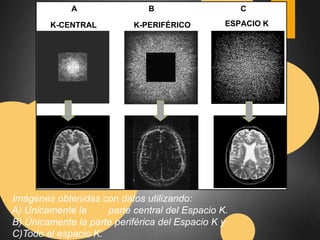
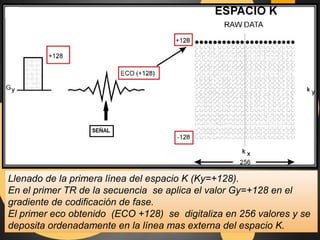
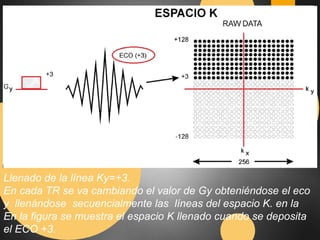
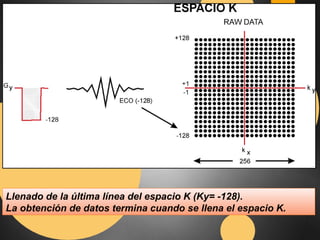
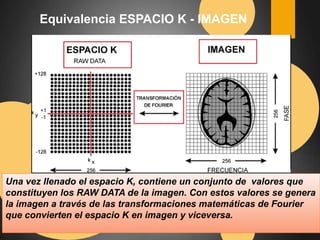
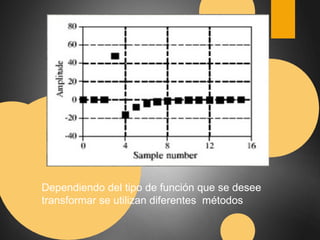
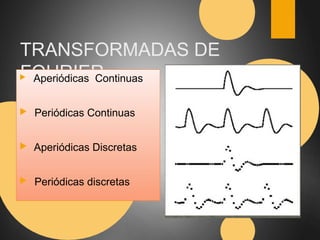
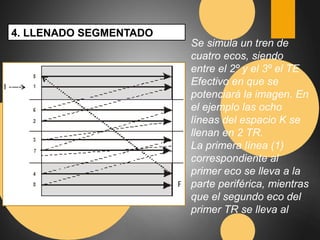
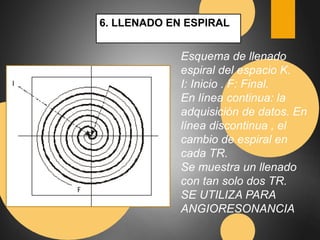
Este documento describe el espacio K en resonancia magnética. El espacio K es el conjunto de datos ordenados formados por los valores digitalizados de los ecos que se utilizan para obtener la imagen. La imagen final se obtiene aplicando transformadas de Fourier al espacio K. El documento explica cómo se organiza y llena el espacio K, incluyendo diferentes formas de llenado como secuencial, con scrolling, concéntrico y en espiral.

1. ESPACIO K
PRESENTADO A:
MILTON MARINO
LOPEZ B.
REALIZADO POR:
FERNANDO
DELGADO
UNIVERSIDAD MARIANA
FACULTAD CIENCIAS DE LA SALUD
PROGRAMA TECNOLOGIARADIODIAGNOSTICO Y RADIOTERAPIA
RESONANCIA MAGNETICA
2014

2. ESPACIO K
▶ La razón del nombre ESPACIO K, reside en que la letra K es
utilizada comúnmente en términos matemáticos y se puede
establecer una similitud entre la fórmula de la señal de resonancia
obtenida en un volumen con la transformada de Fourier en el tiempo.
▶ Es el conjunto de datos ordenados formados por los valores
digitalizados por los ecos con los que se van a obtener la imagen.

3. MATRIZ
Es el soporte de la imagen, esta conformada por los Pixeles y
voxeles a diferencia de la matriz en TAC, esta matriz de RM tiene
FASE y FRECUENCIA esto significa que puedo obtener matrices
rectangulares y se maneja en porcentajes

4. FRECUENCIA DE
MATRIZ
Es el numero de columnas de
izquierda a derecha
FASE
Es el numero de filas de abajo hacia
arriba
Para la Obtención de la imagen en RM.
Debe realizarse la separación de las filas y
columnas de la matriz mediante la
aplicación de gradientes en los ejes "x" e "y"
respectivamente.

5. ▶ La aplicación del gradiente de fase el eje Y permitirá la codificación
de la fase en cada una de las líneas 1, 2 y 3

6. ▶ La aplicación de gradiente en eje X permite codificar en
frecuencia en cada una de las columnas

7. ▶ Cada protón en función de su fase y frecuencia se ubican
en su línea y columna

8. ASPECTOS DEL ESPACIO K

9. A B C
K-CENTRAL K-PERIFÉRICO ESPACIO K
Imágenes obtenidas con datos utilizando:
A) Únicamente la parte central del Espacio K.
B) Únicamente la parte periférica del Espacio K y
C)Todo el espacio K.

10. RAW DATA. Conjunto de datos almacenados de los
que se obtendrá la imagen.
Matriz. Conjunto de datos numericos ordenados =
Espacio K = formado por filas y columnas.
FILAS. Número de codificaciones del gradiente de
fase (DIM-FASE).
COLUMNAS. Viene dado por el número de valores en
que se digitaliza el eco (DIM-FREC) Kx.

11. Ejemplo:
matriz de adquisición de 256 (fase) x 256
(frecuencia)
La imagen se obtendrá mediante 256 valores en el
gradiente de fase (Gy variará desde el valor que
corresponde a Gy= +128 hasta el valor que
corresponde a Gy= -128) y el muestreo de cada
eco generará 256 valores
El conjunto de los Ky (256).Kx (256) valores
depositados ordenadamente en el ESPACIO K
constituyen los RAW DATA con los que se genera
la imagen final mediante las
TRANSFORMACIONES DE FOURIER

12. Llenado de la primera línea del espacio K (Ky=+128).
En el primer TR de la secuencia se aplica el valor Gy=+128 en el
gradiente de codificación de fase.
El primer eco obtenido (ECO +128) se digitaliza en 256 valores y se
deposita ordenadamente en la línea mas externa del espacio K.

13. Llenado de la línea Ky=+3.
En cada TR se va cambiando el valor de Gy obteniéndose el eco
y llenándose secuencialmente las líneas del espacio K. en la
En la figura se muestra el espacio K llenado cuando se deposita
el ECO +3.

14. Llenado de la última línea del espacio K (Ky= -128).
La obtención de datos termina cuando se llena el espacio K.

15. Equivalencia ESPACIO K - IMAGEN
Una vez llenado el espacio K, contiene un conjunto de valores que
constituyen los RAW DATA de la imagen. Con estos valores se genera
la imagen a través de las transformaciones matemáticas de Fourier
que convierten el espacio K en imagen y viceversa.

16. TRANSFORMACIONES DE
FOURIER
Este nombre se debe a Jean Baptiste Fourier
Contribuyo a la idea de que una función puede ser
representada por la suma de funciones sinusoidales
Para obtener una imagen hay que someter la
información del espacio K a procesos matemáticos
para producir una imagen y este proceso toma un
tiempo.

17. Dependiendo del tipo de función que se desee
transformar se utilizan diferentes métodos

18. TRANSFORMADAS DE
FOURIER ▶ Aperiódicas Continuas
▶ Periódicas Continuas
▶ Aperiódicas Discretas
▶ Periódicas discretas

19. Los valores del espacio K darán
lugar a la imagen final después
de realizarse una doble
transformación inversa de
Fourier que permita identificar
cada valor de gris en su posición
en la imagen.

20. ORGANIZACIÓN DEL ESPACIO K.
Trayectoria de llenado
FORMA SECUENCIAL los ecos obtenidos con
frecuencias bajas (valores bajos en la codificación del
gradiente de fase) ocupan el centro del espacio K,
mientras que las altas frecuencias ocupan la
periferia.
La zona central del ESPACIO K contiene la
RESOLUCION DE CONTRASTE, mientras que las
zonas periféricas contienen la RESOLUCION
ESPACIAL.

21. Organización del espacio
K.
Las líneas centrales
obtenidas con los valores
menores de Gy (bajas
frecuencias) contribuyen
principalmente al
contraste en la imagen,
mientras que las líneas
periféricas, obtenidas con
los valores mayores de
Gy (frecuencias altas)
contribuyen
principalmente en la
resolución espacial.

22. FORMAS DE LLENADO DEL ESPACIO
K.

23. 1. LLENADO SECUENCIAL
Esquema del llenado
secuencial estándar del
espacio K.
Se inicia en el punto I
correspondiente a la línea
mas externa y se van
llenando las línea
sucesivas siempre
empezando por el mismo
lado.
Termina el llenado en el
punto F.
En trazo continuo el
llenado de datos.
En trazo discontinuo el
seguimiento de los
cambios de posición.

24. 2. LLENADO SECUENCIAL CON SCROLLING
Esquema del llenado
secuencial con scrolling
del espacio K.
I: Inicio del llenado, F
final.
En línea continua la
toma de datos.
En línea discontinua los
cambios de posición

25. 3. LLENADO CONCENTRICO
Esquema del llenado
concéntrico del espacio
K.
I: punto de partida, F
final.
En línea continua el
llenado de datos.
En línea discontinua, los
cambios de posición.
Cada línea se llena en un
TR.
El espacio K se llena
después de haber
preparado previamente
el tejido.

26. 4. LLENADO SEGMENTADO
Se simula un tren de
cuatro ecos, siendo
entre el 2º y el 3º el TE
Efectivo en que se
potenciará la imagen. En
el ejemplo las ocho
líneas del espacio K se
llenan en 2 TR.
La primera línea (1)
correspondiente al
primer eco se lleva a la
parte periférica, mientras
que el segundo eco del
primer TR se lleva al

27. 5. LLENADO ZIG – ZAG
Esquema del llenado
del espacio K utilizando
una forma EPI SINGLE
SHOT RESONANT. O
ZIG-ZAG
I: Inicio. F: Final.
En línea continua la
adquisición de datos.
ES EL MAS UTILIZADO
EN LAS
SECUAENCIAS
MODERNAS

28. 6. LLENADO EN ESPIRAL
Esquema de llenado
espiral del espacio K.
I: Inicio . F: Final.
En línea continua: la
adquisición de datos. En
línea discontinua , el
cambio de espiral en
cada TR.
Se muestra un llenado
con tan solo dos TR.
SE UTILIZA PARA
ANGIORESONANCIA

29. Bibliografías
• http://
nuclear.fis.ucm.es/research/thesis/TM-Rosa-Gantes.pdf
• http://
www.scielo.cl/scielo.php?script=sci_arttext&pid=S0717-93082009000400002
• http://
books.google.com.co/books?id=7RBvSRdFuBMC&pg=PA24&dq=• http://books.google.com.co/books?id=mN-dAwAAQBAJ&
pg=PA46&dq=espacio+k&hl=es&sa
=X&ei=zjYVVLHOJK7CsAS_74KoAg&ved=0CDQQ
6wEwBA#v=onepage&q=espacio%20k&f=false

30. ▶GRACIAS