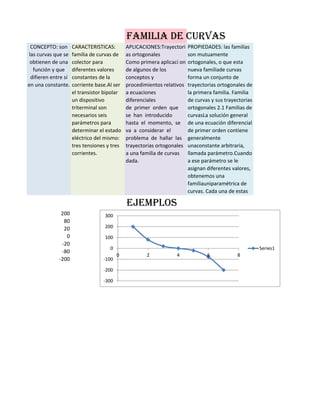
Este documento describe las familias de curvas, que son curvas obtenidas de una función que difieren solo en una constante. Las familias de curvas tienen propiedades como ser mutuamente ortogonales y forman conjuntos de trayectorias ortogonales entre sí. Un ejemplo de aplicación es hallar las trayectorias ortogonales a una familia de curvas dada.

1. FAMILIA DE CURVAS
CONCEPTO: son
las curvas que se
obtienen de una
función y que
difieren entre sí
en una constante.
CARACTERISTICAS:
familia de curvas de
colector para
diferentes valores
constantes de la
corriente base.Al ser
el transistor bipolar
un dispositivo
triterminal son
necesarios seis
parámetros para
determinar el estado
eléctrico del mismo:
tres tensiones y tres
corrientes.
APLICACIONES:Trayectori
as ortogonales
Como primera aplicaci on
de algunos de los
conceptos y
procedimientos relativos
a ecuaciones
diferenciales
de primer orden que
se han introducido
hasta el momento, se
va a considerar el
problema de hallar las
trayectorias ortogonales
a una familia de curvas
dada.
PROPIEDADES: las familias
son mutuamente
ortogonales, o que esta
nueva familiade curvas
forma un conjunto de
trayectorias ortogonales de
la primera familia. Familia
de curvas y sus trayectorias
ortogonales 2.1 Familias de
curvasLa solución general
de una ecuación diferencial
de primer orden contiene
generalmente
unaconstante arbitraria,
llamada parámetro.Cuando
a ese parámetro se le
asignan diferentes valores,
obtenemos una
familiauniparamétrica de
curvas. Cada una de estas
curvas es solución de la
EJEMPLOS
200
80
20
0
-20
-80
-200
-300
-200
-100
0
100
200
300
0 2 4 6 8
Series1