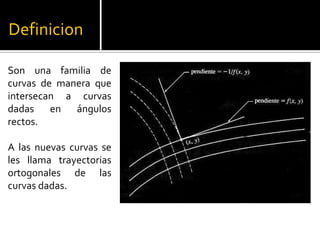
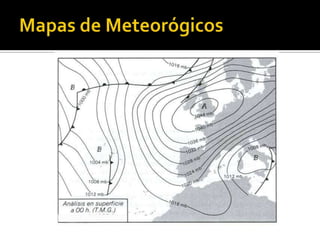
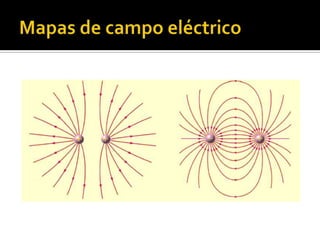
Las ecuaciones diferenciales se utilizan para representar familias de curvas donde cada curva es una solución de la ecuación diferencial. Las trayectorias ortogonales a estas curvas también son soluciones y representan flujos como el calor o campo eléctrico. Los diagramas de líneas de campo como las líneas eléctricas y magnéticas ayudan a visualizar campos que no se pueden ver directamente.

1. Aplicaciones de las Ecuaciones Diferenciales

2. Definicion
Son una familia de
curvas de manera que
intersecan a curvas
dadas en ángulos
rectos.
A las nuevas curvas se
les llama trayectorias
ortogonales de las
curvas dadas.

3.  La solución general de una ecuación
diferencial de primer orden contiene
generalmente una constante
arbitraria, llamada parámetro.
F(x, y, c) = 0
 Cada una de estas curvas es solución de la
ecuación diferencial dada y todas juntas
constituyen la solución general.

4.  Dada una familia de la forma de la ecuación,
se encuentra su ecuación diferencial de la
forma:
 Se encuentran las trayectorias ortogonales
resolviendo su ecuación diferencial:

5.  La familia de curvas en coordenadas polares
tiene la forma:
 Obtenemos la ecuación diferencial de la
familia de curvas:

6.  Y finalmente obtenemos la familia de
trayectorias ortogonales resolviendo la
ecuación diferencial:

9.  Las curvas representan isobaras las cuales son
curvas que conectan todos los puntos que tienen
la misma presión barométrica.
 En vez de isobaras las curvas de la figura anterior
podrían representar curvas isotérmicas.
 En tal caso las trayectorias ortogonales
representa la dirección general del flujo de calor.

11.  El concepto de campo eléctrico es un tanto
elusivo debido a que ningún campo eléctrico
puede verse directamente.
 Para visualizarlos, las líneas de campo
eléctrico son de gran ayuda y los hace parecer
más reales.

12.  El concepto de campo eléctrico es un tanto
elusivo debido a que ningún campo eléctrico
puede verse directamente.
 Para visualizarlos, las líneas de campo
eléctrico son de gran ayuda y los hace parecer
más reales.

13.  Las líneas de campo eléctrico muestran la
dirección de E en cada punto, y su
espaciamiento da una idea general de la
magnitud de en cada punto.
 En cualquier punto específico, el campo
eléctrico tiene dirección única, en otras
palabras, las líneas de campo nunca se cruzan.

14.  A veces estos diagramas reciben el nombre
de mapas de campo; son secciones
transversales de los patrones reales en tres
dimensiones.
 En un campo eléctrico las líneas de fuerza son
las trayectorias ortogonales de las líneas de
equipotencial (curvas de voltaje constante).

16.  Cualquier campo magnético se representa
usando líneas de campo magnético. La idea
es la misma que para las líneas de campo
eléctrico.