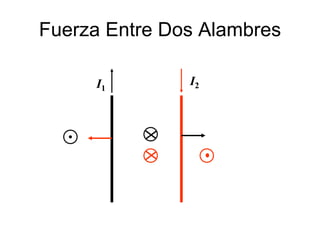
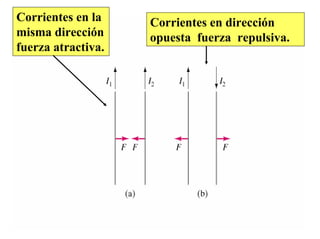
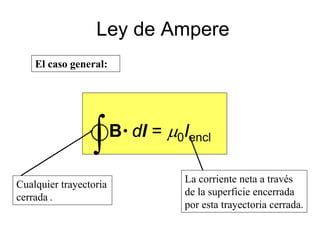
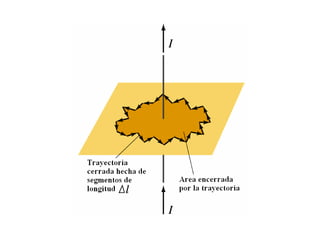
La ley de Biot-Savart describe cómo un elemento de corriente genera un campo magnético en un punto. El documento también resume fórmulas para el campo magnético creado por alambres rectos, lazos de corriente circular y solenoides, así como la ley de Ampere y la fuerza entre alambres paralelos.




![∫=
2
1
2
4
θ
θ
θ
π
µ
r
dxsenI
B o
r
∫=
2
1
22
2
csc
csc
4
θ
θ θ
θθθ
π
µ
a
dsenaI
B o
r
∫=
2
14
θ
θ
θθ
π
µ
dsen
a
I
B o
r
( )21
coscos
4
θθ
π
µ
−=
a
I
B o
r
Alambre recto finito
πθθ == 21
y0Alambre recto infinito
( ) ( )[ ]11
4
cos0cos
4
−−=−=
a
I
a
I
B oo
π
µ
π
π
µr
a
I
B o
π
µ
2
=
r](https://image.slidesharecdn.com/selection1-151029041645-lva1-app6891/85/Selection-1-5-320.jpg)