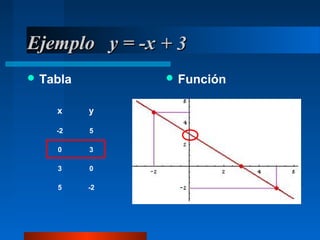
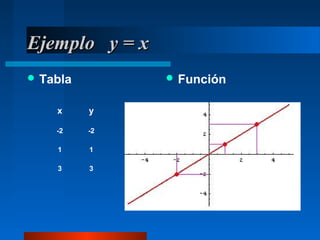
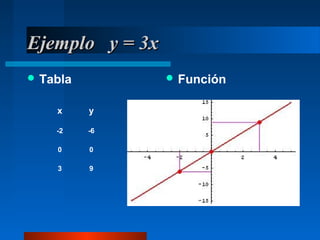
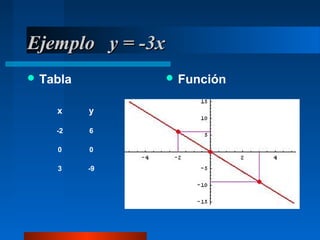
El documento explica las funciones afines y lineales, incluyendo sus ecuaciones y representaciones gráficas. Define la pendiente y la ordenada en el origen de una función afín, y cómo estas características determinan si la recta es creciente o decreciente. También cubre las diferentes formas de escribir la ecuación de una recta y ejemplos de cómo convertir entre ellas.

1. RECTAS PARA 3º E.S.O.
4
2 y = mx + n
-4 -2 2 4 6
-2
-4

2. Función afín
 Ecuación y = mx + n
• m es la pendiente
 Si m = 0 se llama función constante con
ecuación y = n
 Cuanto mayor es el valor absoluto de m,
mayor es la inclinación de la recta.
• n es la ordenada en el origen.
 Ejemplos y=x+3
y = 5x - 2
y = -x + 3

3. Ejemplo y = x + 3
 Tabla  Función
x y
-2 1
0 3
3 6

4. Ejemplo y = 5x - 2
 Tabla  Función
x y
-1 -7
0 -2
1 3
2 8

5. Ejemplo y = -x + 3
 Tabla  Función
x y
-2 5
0 3
3 0
5 -2

6. Todos los ejemplos juntos
Función Analogías
– Ninguna pasa por el
y = 5x - 2
punto (0,0)
y = -x + 3 y=x+3
– Pasan por el punto (0,n)
Diferencias
– Si m>0 la recta es
creciente
– Si m<0 la recta es
A mayor m en módulo, mayor es la decreciente
inclinación de la recta

7. Función lineal
(n = 0)
 Ecuación y = mx
• m es la pendiente
 Ejemplos y=x
y = 3x
y = -3x

8. Ejemplo y = x
 Tabla  Función
x y
-2 -2
1 1
3 3

9. Ejemplo y = 3x
 Tabla  Función
x y
-2 -6
0 0
3 9

10. Ejemplo y = -3x
 Tabla  Función
x y
-2 6
0 0
3 -9

11. Todos los ejemplos juntos
Función Analogías
– Todas pasan por el
y = 3x
y = -3x punto (0,0)
y=x
Diferencias
– Si m>0 la recta es
creciente
– Si m<0 la recta es
decreciente
A mayor m en módulo, mayor es la
inclinación de la recta

12. Estudio de la pendiente
 Considera la recta que
pasa por el origen y
forma un ángulo de
inclinación con el eje
x.
 Como los triángulos de
catetos
x1 y1 , x2 y2 y x3 y3
son semejantes; se tiene y1 y2 y3
por Tales que: = = =m
x1 x2 x3

13. Ecuaciones de la recta
 Explícita
 Punto pendiente
 Recta que pasa por dos puntos
 General

14. Explícita
y = mx + n
 Ejemplo. Halla la recta de pendiente
5 y de ordenada en el origen -3.
• Sol: y = 5x - 3

15. Punto pendiente
y - y0= m(x - x0)
 Ejemplo. Halla la recta que pasa por el
punto (1,-2) y tiene por pendiente -1.
• Sol: y - (-2) = -1(x - 1)
y + 2 = -x + 1
y = -x - 1

16. Recta que pasa por dos puntos
 La
pendiente de la recta que pasa por los
puntos P =(x0,y0) y Q =(x1,y1) es
y1 − y0
m=
x1 − x0
 Dados los puntos (0,1) y (-2,5) de una recta,
halla su pendiente.
• Sol:
5 −1 4
m= = = −2
−2−0 −2

17. General
 ax+by+c=0
 Si despejamos en la ecuación el valor de
y, nos queda:
−a c
y= x−
b b
m n

18. Ejemplos de ecuaciones de la recta
Ejemplo 1
Sea la ecuación explícita de la recta r
y = 5x – 3
Halla las restantes ecuaciones de dicha recta.
• General
• Punto pendiente
• Recta que pasa por dos puntos

19. Solución del ejemplo 1
• General: y - 5x – 3 = 0
• Punto pendiente. Se ve en la ecuación explicita que la
pendiente es 5 y elijo un punto que cumpla la recta (1,2).
y – 2 = 5 (x - 1)
• Recta que pasa por dos puntos. Elijo dos puntos
que cumplan la recta para hallar la pendiente. A (1,2) y B (2,7)
7−2 5 Ahora uso la ecuación
m= = =5 de la recta pendiente
2 −1 1 y – 1 = 5 (x - 2)

20. Ejemplos entre las diferentes
ecuaciones de la recta
Ejemplo 2
Sea la ecuación general de la recta r
4x + 2y - 6 = 0
Halla las restantes ecuaciones de dicha recta.
• Explícita
• Punto pendiente
• Recta que pasa por dos puntos

21. Solución del ejemplo 2
• Explícita: y = - 2x + 3
• Punto pendiente. Se ve en la ecuación explicita que la
pendiente es -2 y elijo un punto que cumpla la recta (2,-1).
y + 1 = -2 (x - 2)
• Recta que pasa por dos puntos. Elijo dos puntos
que cumplan la recta para hallar la pendiente. A (2,-1) y B (4,-5)
− 5 − (−1) − 4 Ahora uso la ecuación
m= = = −2 de la recta pendiente
4−2 2 y – 1 = 5 (x - 2)

22. Ejercicio 1
• En el arreglo de una persiana se invierten 30
minutos.
• a) Realiza una tabla que muestre el tiempo
necesario para arreglar 2, 3, 5 y 10 persianas.
• b) Representa la gráfica acorde con estos datos.
• c) Halla la expresión analítica de la función.
• d) ¿Hay relación entre el tiempo y el número de
persianas arregladas? ¿De qué tipo?

23. Ejercicio 2
• Al realizar un viaje en taxi, el conductor cobra una
cantidad fija (bajada de bandera) de 3 euros y una
cantidad variable que depende de la duración del
viaje. Cada minuto cuesta 0.75 euros.
• a) Realiza una tabla que muestre el coste de un trayecto de 5,
10, 20 y 30 minutos.
• b) Representa la gráfica acorde con estos datos.
• c) Halla la expresión analítica de la función.
• d) Si disponemos de un máximo de 20 euros ¿cuánto tiempo
durará el viaje?

24. Posiciones relativas de dos rectas en
el plano
Dos rectas cualesquiera del plano pueden adoptar
una de estas tres posiciones relativas.
c)
b)
a) Rectas paralelas (se cortan)
secantes
coincidentes
y
• 5
4
Son rectas con misma pendiente y
distinta pendiente
3
misma ordenada en el origen
distintaordenada en el origen
2 •
1
-1 1 2 3 4 x
-1 L