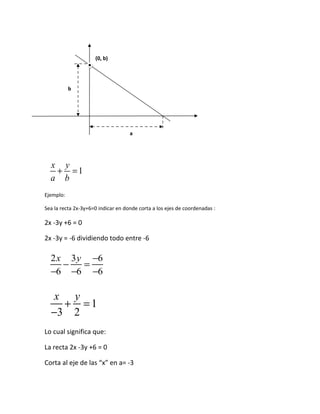
El documento describe diferentes formas de expresar la ecuación de una recta: 1) ecuación general de primer grado, 2) ecuación punto-pendiente, 3) ecuación ordenada al origen, y 4) ecuación simétrica. También explica cómo calcular la pendiente y los puntos de corte con los ejes usando cualquiera de estas formas de la ecuación.

1. LA LÍNEA RECTA.
La recta se expresa analíticamente como una ecuación lineal o de primer grado con dos variables y
queda determinada si se conocen dos condiciones:
• 2 puntos por donde pasa.
• La pendiente y un punto que pertenezcan a ella-
Existen varias formas de la ecuación de la recta.
ECUACIÓN EN FORMA GENERAL DE LA RECTA:
Expresión de de primer grado con dos variables.
Ax +By + C = 0 en donde A, B y C son constantes arbitrarias y “x” y “y” las variables.
A
La pendiente está determinada por la expresión: m=−
B
C
Y el punto donde la recta corta al eje de la y (ordenada al origen) es b= −
B
.
ECUACIÓN PUNTO PENDIENTE:
Recordando la fórmula para obtener la pendiente de una recta, conociendo dos puntos por donde
pasa se tiene:
A(x,y)
α y-y1 y
B(x1,y1) y1
x1 x-x1
x

2. La pendiente es el ángulo de inclinación con respecto al eje de las “x”, por lo
tanto se obtiene:
y − y1
tan α = =m Así tenemos:
x − x1
y − y1
m=
x − x1
Por lo tanto La Ecuación en forma Punto Pendiente se obtiene:
( x − x1 ) m = y − y1
ECUACIÓN EN FORMA ORDENADA AL ORIGEN
P(x,y)
(0, b)
b
y−b
m= ( x − 0)
x−0
m( x − 0) = y − b
mx + b = y
o bien y = mx + b

3. Ejemplo Encontrar la pendiente y el punto donde la recta 2x-3y+6 =0 corta al
eje “y”:
2x-3y+6=0
Como la expresión dice y = mx +b se despejará “y”
2 x −3 y +6 =0
− y +6 =− x
3 2
− y =− x −6
3 2
2
− x −6
2 Donde la pendiente m =
y= 3
−3
2 6
y =− x + Y el punto donde la recta corta al eje “y”= 2
3 3
2
y = x +2
3
b=2
3
Cuando la pendiente de una recta es positiva quiere decir que dicha inclinación es menor a 90º
cuando se obtiene una pendiente con signo negativo esto quiere decir que la inclinación es mayor
de 90º.
ECUACIÓN SIMÉTRICA O ABSCISA Y ORDENADA AL ORIGEN.
Esta ecuación trabaja con los valores de a y de b que son, respectivamente la abscisa y la ordenada
al origen; dicho de otra manera, los puntos en donde una recta corta a los ejes de coordenadas.
Si los puntos son A(a,0) y B(0,b)

4. (0, b)
b
a
x y
+ =1
a b
Ejemplo:
Sea la recta 2x-3y+6=0 indicar en donde corta a los ejes de coordenadas :
2x -3y +6 = 0
2x -3y = -6 dividiendo todo entre -6
2x 3y −6
− =
−6 −6 −6
x y
+ =1
−3 2
Lo cual significa que:
La recta 2x -3y +6 = 0
Corta al eje de las “x” en a= -3

5. Y al eje “y” en b= 2
b=2
a = -3
LA ECUCIÓN EN FORMA NORMAL O DE HESSE
La recta puede determinarse, además, si se conocen la longitud de su perpendicular trazada a
ella desde el origen y el ángulo que dicha perpendicular forma con el eje “x’ x”.
(NO SE HARÁ LA DEMOSTRACIÓN).
Se podrá escribir que la forma normal de Ax + By + C = 0 es
Ax By C
+ + = 0.
± A +B 2 2
± A +B2 2
± A +B 2 2
Para determinar el signo que se debe dejar al radical se seguirá el siguiente criterio:
a) Será siempre opuesto al de C.
b) Sí C = 0, se considerará el signo que tenga B
Ax + By + C
Ejemplo: Distancia de un punto a una recta. d=
± A2 + B 2
Hallar la distancia del punto (-2,-4) a la recta 6x – 8y +5 = 0

6. 6x − 8 y + 5
=0
− 6 2 + 82
6x − 8 y + 5
=0
− 100
6x − 8 y + 5
=0
− 10
6(− 2) − 8(− 4) + 5
=0
− 10
− 12 + 32 + 5
=0
− 10
− 12 + 32 + 5 25
= = − 2.5ul
− 10 − 10
La distancia resulta negativa, significando que el punto y el origen están del mismo lado.
P