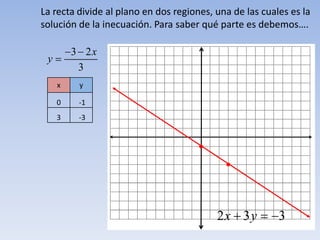
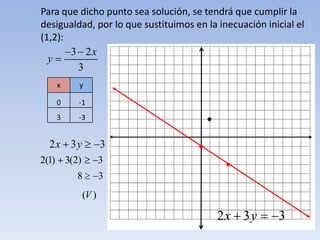
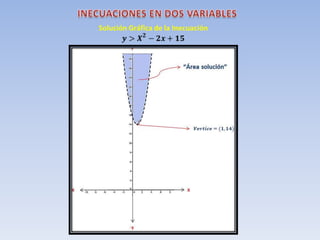
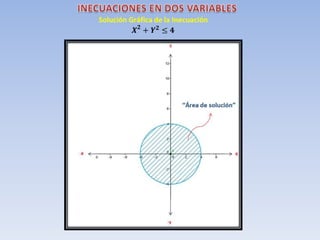
Este documento define una inecuación lineal con dos variables como una expresión de la forma ax + by ≤ c, donde a, b y c son números reales y x e y son las incógnitas. Explica que la recta definida por la inecuación divide el plano en dos regiones, una de las cuales es la solución. Para determinar cuál es la región solución, se toma un punto cualquiera y se comprueba si cumple o no la inecuación original. Si es cierta para ese punto, entonces la región que lo contiene es la soluc

2. Definición
Una inecuación lineal con 2 variables es una
expresión de la forma:
Donde :
•
•
•
El símbolo ≤ puede ser también ≥ , < o bien >
a, b y c son números reales
x e y las incógnitas.
ax + by ≤ c

6. La recta divide al plano en dos regiones, una de las cuales es la
solución de la inecuación. Para saber qué parte es debemos….
3 2x
y
3
2x 3y 3
x y
0 -1
3 -3

7. Tomar un punto cualquiera
ejemplo el (1,2).
que no pertenezca a la recta, por
3 2x
y
3
2x 3y 3
x y
0 -1
3 -3

8. Para que dicho punto sea solución, se tendrá que cumplir la
desigualdad, por
(1,2):
lo que sustituimos en la inecuación inicial el
3 2x
y
3
2x 3y 3
2(1) 3(2) 3
8 3
(V )
2x 3y 3
x y
0 -1
3 -3

9. Como está ultima desigualdad es cierta, concluimos que el
semiplano que contiene
semiplano superior,.
3 2x
al (1,2) es la solución, es decir el
y
3
2x 3y 3
2(1) 3(2) 3
8 3
(V )
2x 3y 3
x y
0 -1
3 -3

10. Ahora, sólo faltaría achurar el semiplano que se encuentra por
encima de la recta 2x + 3y = -3
3 2x
y
3
Solución de:
2x + 3y ≥ −3
2x 3y 3
2(1) 3(2) 3
8 3
(V )
2x 3y 3
x y
0 -1
3 -3

15. Resolver el bloque de
ejercicios propuestos
6.9. en las págs.:
186 y 187 del texto de
Edwin Galindo
«Matemáticas
Superiores»