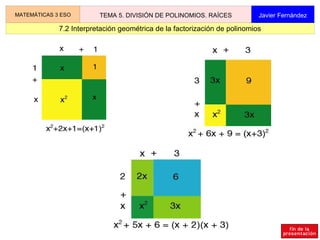
El documento proporciona información sobre la división de polinomios. Explica cómo dividir polinomios por monomios y cómo realizar la división entera de polinomios. También describe la regla de Ruffini para dividir un polinomio por (x-a) y los teoremas del resto y del factor. Finalmente, cubre cómo calcular las raíces de un polinomio y factorizar polinomios.

1. 1. División de polinomios por monomios MATEMÁTICAS 3 ESO TEMA 5. DIVISIÓN DE POLINOMIOS. RAÍCES Javier Fernández El cociente de dos monomios (si es posible) es igual a otro monomio que tiene: como coeficiente , el cociente de los coeficientes;

2. como parte literal , las letras que aparecen en el dividendo,

3. cada una con exponente igual a la diferencia del exponente

4. del dividendo y del divisor. no es un un polinomio El cociente de un polinomio por un monomio (si es posible) es igual a un polinomio cuyos términos son los que se obtienen dividiendo cada término del polinomio por el monomio.

5. 2.1 División entera de polinomios MATEMÁTICAS 3 ESO TEMA 5. DIVISIÓN DE POLINOMIOS. RAÍCES Javier Fernández Dados los polinomios dividendo D(x) y divisor d(x)  0, didivir D(x) entre d(x) es encontrar dos polinomios cociente C(x) y resto R(x) tales que D(x) = d(x) . C(x) + R(x) que se suele esquematizar de la siguiente manera: Si el resto R(x)= 0 la división se llama exacta , y se dice que

6. el polinomio D(x) es divisible por d(x) o múltiplo de d(x); o que

7. d(x) es un factor de D(x), o divisor de D(x). D(x) d(x) C(x) R(x)

8. 2.2 Ejemplo de división entera MATEMÁTICAS 3 ESO TEMA 5. DIVISIÓN DE POLINOMIOS. RAÍCES Javier Fernández x 3 3x 5 + 8x 4 – 11x 2 – 3x + 6 – (3x 5 + 2x 4 –4x 3 ) 6x 4 + 4x 3 – 11x 2 – 3x + 6 Primer paso – ( 6x 4 + 4x 3 – 8x 2 ) – 3x 2 – 3x + 6 – x + 2 + 2x 2 – 1 La división entera de polinomios se realiza del mismo modo que la división entera de números naturales. resto – (– 3x 2 – 2x + 4) Se resta (–1) . d cociente Cociente de los términos de mayor grado Cociente de los términos de mayor grado 3x 2 +2x–4 3x 5 + 8x 4 – 11x 2 – 3x + 6 3x 2 +2x–4 x 3 – (3x 5 + 2x 4 –4x 3 ) 6x 4 – 4x 3 – 11x 2 – 3x + 6 Segundo paso 3x 5 + 8x 4 – 11x 2 – 3x + 6 3x 2 +2x–4 x 3 + 2x 2 – (3x 5 + 2x 4 –4x 3 ) 6x 4 – 4x 3 – 11x 2 – 3x + 6 – ( 6x 4 – 4x 3 – 11x 2 ) – 3x 2 – 3x + 6 Tercer paso Se resta x 3 . d Se resta 2x 2 . d Cociente de los términos de mayor grado

9. 3. División por x-a. Regla de Ruffini MATEMÁTICAS 3 ESO TEMA 5. DIVISIÓN DE POLINOMIOS. RAÍCES Javier Fernández Para dividir un polinomio P = 2x 3 – 6x 2 – 4x + 12 entre x – 2 se puede usar el siguiente esquema llamado Regla de Ruffini 2 – 6 – 4 12 2 Se opera: 4 – 2 – 4 – 8 – 16 – 4 Hemos obtenido que: P = 2x 3 – 7x 2 – 4x + 12 = (2x 2 – 2x – 8) (x – 2) + (– 4) r se suma se multiplica por a Coeficientes de P a 2 – 6 – 4 12 2 2

10. 4.1 Teorema del resto MATEMÁTICAS 3 ESO TEMA 5. DIVISIÓN DE POLINOMIOS. RAÍCES Javier Fernández Al dividir P(x) entre x – a obtenemos: Es decir: P(x) = (x – a) C(x) + R Luego P(a) = (a – a) C(a) + R = R El resto de dividir un polinomio P(x) por (x – a) es igual al valor numérico del polinomio P(x) para x = a; es decir R = P(a) El resto de dividir P(x) = 2x 3 – 7x 2 – 4x + 12 entre x – 2 se puede obtener así: P(2) = 2 . 2 3 – 7 . 2 2 – 4 . 2 + 12 = – 4 P(x) x – a C(x) R