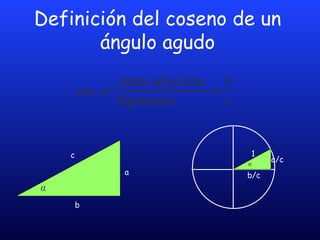
Este documento trata sobre la historia y conceptos básicos de la trigonometría. Explica que la trigonometría se utiliza para resolver problemas relacionados con triángulos, como determinar lados desconocidos. Define las funciones trigonométricas como relaciones entre los lados de un triángulo rectángulo y presenta ejemplos de problemas trigonométricos y sus soluciones.

1. Tema t rigonometría

4. a c b Si conocemos dos de los lados del triángulo, como el Teorema de Pitágoras afirma que a 2 + b 2 = c 2 , Comencemos con triángulos rectángulos. conocemos el tercer lado. Eso sí, debemos saber si los lados que conocemos son catetos o la hipotenusa.

6. La figura muestra las funciones trigonométricas asociadas a un ángulo agudo ubicado en una circunferencia secante cosecante radio seno tangente cotangente coseno

7. Definición del seno de un ángulo agudo a b c b/c a/c 1

8. Definición del coseno de un ángulo agudo a b c b/c a/c 1

9. Funciones trigonométricas: secante y cosecante de un ángulo agudo a b c b/c a/c 1

10. Todas las funciones trigonométricas de un ángulo agudo pueden expresarse a partir de una de ellas, a modo de ejemplo tomemos sen = = = = =

11. Identidades Trigonométricas 1 cos sen La identidad fundamental es consecuencia del Teorema de Pitágoras

12. Identidades Trigonométricas 1 Si es el ángulo complementario de , hay un triángulo rectángulo que los tiene como ángulos agudos y se tiene que cos sen

13. Funciones Trigonométricas de ángulos arbitrarios Para calcular el seno (o el coseno) de un ángulo agudo , colocamos un triángulo rectángulo como en la figura. El seno (o coseno) del ángulo es la ordenada (o la abscisa) del punto de intersección de la hipotenusa con el círculo. Pero no es necesario tener todo el rectángulo, basta con tener la recta que une con el origen.

14. Funciones Trigonométricas de ángulos arbitrarios DEFINIMOS para un ángulo , medido a partir de la recta contra las manecillas del reloj: l la abscisa de la ordenada de l

15. Funciones Trigonométricas de ángulos arbitrarios l  en cuadr. I II III IV sen  + + - - cos  + - - + tan  + - + -

16. Actividad I… Construir un triángulo cuyos lados sean de longitud 3, 4 y 5 . Comparar los distintos triángulos que se obtienen. Nota: cada quien es libre de escoger la escala

17. Problema En una circunferencia de centro O y radio 5 está trazada una cuerda que mide 3.5 ¿cuánto mide el ángulo central asociado? En la misma circunferencia, halle la longitud de la cuerda subtendida por un ángulo de 72 o . O 5

18. Problema Una cuerda de 100m de largo se estira un metro más y se sostiene del centro (ver la figura). ¿ A qué altura se encuentra el punto C? Dé una medida aproximada del ángulo . 100m 101m C

19. Pregunta a b c ¿ Cuáles son los valores máximo y mínimo de la función coseno ? ¿Alguno de los catetos puede ser mayor que la hipotenusa? ¿ Cuáles son los valores máximo y mínimo de la función seno ? ¿ Cuáles son los valores máximo y mínimo de la función tangente ?

20. SIGNO DE LAS RAZONES EN LOS CUATRO CUADRANTES I II III IV sen(  ) + + - - cos(  ) + - - + tan(  ) + - + -