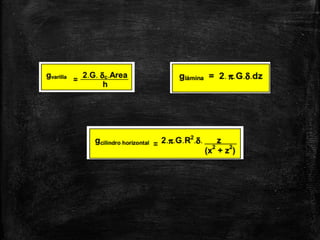
1. La gravedad es la atracción gravitacional que ejerce la masa de la Tierra sobre los cuerpos en su superficie. 2. Isaac Newton estableció las tres leyes del movimiento y determinó que la fuerza gravitatoria disminuye con el cuadrado de la distancia. 3. En 1798, Henry Cavendish midió experimentalmente el valor de la constante de gravitación universal G usando una balanza de torsión.