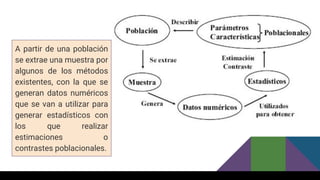
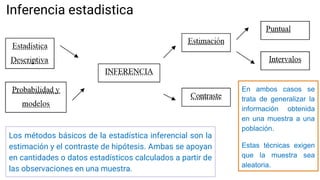
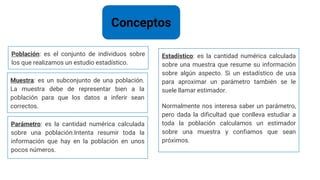
Este documento presenta una introducción a la inferencia estadística. Explica que la inferencia estadística se ocupa de predecir y sacar conclusiones sobre una población a partir de una muestra. Define conceptos clave como población, muestra, parámetro, estadístico. También describe diferentes métodos de muestreo como el aleatorio simple, sistemático, estratificado y por conglomerados. Finalmente, introduce la estimación puntual y cómo se puede estimar la media, proporción y varianza de una población a partir de datos mue

1. 2.1 Inferencia Estadistica.
Integrantes:
Jesus Felix Limon Cortes 15100549
Pedro Abraham Moreno Diaz 15100559
Jorge Sifuentes Castillo 15100591
Juan Eduardo Valle Velazquez 15100596
Luis Alejandro Puente Velazquez 15100573

2. Introducción a la
Inferencia Estadística

3. ¿Que es la inferencia estadística?
La inferencia estadística es el conjunto de métodos y técnicas que permiten
inferir, a partir de la información empírica proporcionada por una muestra,
cual es el comportamiento de una determinada población con un riesgo de
error medible en términos de probabilidad.
En pocas palabras la inferencia estadística se ocupa de predecir y sacar
conclusiones sobre una población tomando como base una muestra, es
decir una parte de dicha población.
También es denominada Estadística Inductiva o
Inferencia Inductiva ya que es un procedimiento para
generar nuevo conocimiento científico.

4. ¿Que es la inferencia estadística?
La inferencia estadística es el conjunto de métodos y técnicas que permiten
inferir, a partir de la información empírica proporcionada por una muestra,
cual es el comportamiento de una determinada población con un riesgo de
error medible en términos de probabilidad.
En pocas palabras la inferencia estadística se ocupa de predecir y sacar
conclusiones sobre una población tomando como base una muestra, es
decir una parte de dicha población.
También es denominada Estadística Inductiva o
Inferencia Inductiva ya que es un procedimiento para
generar nuevo conocimiento científico.

5. A partir de una población
se extrae una muestra por
algunos de los métodos
existentes, con la que se
generan datos numéricos
que se van a utilizar para
generar estadísticos con
los que realizar
estimaciones o
contrastes poblacionales.

6. Inferencia estadistica
Los métodos básicos de la estadística inferencial son la
estimación y el contraste de hipótesis. Ambas se apoyan
en cantidades o datos estadísticos calculados a partir de
las observaciones en una muestra.
En ambos casos se
trata de generalizar la
información obtenida
en una muestra a una
población.
Estas técnicas exigen
que la muestra sea
aleatoria.

7. Un fabricante de medicinas afirma que una nueva vacuna contra el catarro
desarrollada por su compañía tiene una efectividad del 95%, esto es, en promedio
95 de cada 100 personas que emplean la vacuna, pasarán el invierno sin
contagiarse de catarro. Como resulta imposible probar la vacuna en todas las
personas, consideremos que 40 personas han recibido la vacuna, y que de las 40,
35 no se contagiaron de catarro.Vemos que si la información del fabricante es
correcta se esperaría que 38 personas (40 x 0.95 = 38) pasarán el invierno sin
catarro.
Puesto que el número observado es 35, lo cual es inferior al número
esperado, ¿debería rechazarse la afirmación del fabricante en base a la
evidencia? El proceso de decisión de rechazar o no la afirmación es un
problema de inferencia estadística.
¿para que la inferencia estadística?

8. Población: es el conjunto de individuos sobre
los que realizamos un estudio estadístico.
Muestra: es un subconjunto de una población.
La muestra debe de representar bien a la
población para que los datos a inferir sean
correctos.
Parámetro: es la cantidad numérica calculada
sobre una población.Intenta resumir toda la
información que hay en la población en unos
pocos números.
Estadístico: es la cantidad numérica calculada
sobre una muestra que resume su información
sobre algún aspecto. Si un estadístico de usa
para aproximar un parámetro también se le
suele llamar estimador.
Normalmente nos interesa saber un parámetro,
pero dada la dificultad que conlleva estudiar a
toda la población calculamos un estimador
sobre una muestra y confiamos que sean
próximos.
Conceptos

9. Muestreo
Dado que en la mayoría de las ocasiones no es posible contar con los datos
completos de una población, es habitual que tengamos que manejarnos con
muestras, de modo que es importante saber elegir bien una muestra de la
población.
Si la muestra está mal elegida, diremos que no es representativa. En este caso, se
pueden producir errores imprevistos denominados sesgos.
Es importante la muestra sea elegida de forma
aleatoria.

10. Básicamente hay dos tipos de muestreos:
1. Muestreo no probabilístico: la muestra se elige mediante determinados
criterios subjetivos.
1. Muestreo probabilístico: Cuando la muestra se elige al azar. En este caso
podemos distinguir varios tipos:

11. a) Muestreo aleatorio simple:
Aquel en el que cada individuo de la población tiene las mismas posibilidades de salir
en la muestra.
Ejemplo:
En una escuela de 600 alumnos elegimos un alumno al azar y su probabilidad de
elegirlo sería de 1/600. Lo devolvemos a la población y se elige otro con las misma
probabilidad de ser elegido 1/600, y asi hasta sacar a 20 alumnos.
Notemos que si no devolvieramos al alumno, entonces, la probabilidad de escoger al
2º alumno sería de 1/599, y ya no todos tendrían la misma probabilidad de ser
elegidos. El problema es que entonces permitimos que se puedan repetir individuos.

12. b) Muestreo sistemático:
En el que se elige un individuo al azar y a partir de él, a intervalos constantes, se eligen
los demás hasta completar la muestra.
Ejemplo:
De 600 alumnos hemos de elegir 20 alumnos, es decir, 1 de cada 30, se procede asi:
Se ordenan los alumnos y se enumeran, se elige uno al azar, por ejemplo el alumno
27, y luego los demás se eligen a partir de este a intervalos de 30 alumnos. Entonces
escogemos por tanto a los alumnos:
27,57,87,117,147,177,207,237,267,297,327,357,387,417,447,477,507,537,567,597 y el
alumno 627 ya es otra vez el 27.

13. c) Muestreo estratificado:
Se divide la población en clases o estratos y se escoge, aleatoriamente, un número de
individuos de cada estrato proporcional al número de componentes de cada estrato.
Ejemplo:
De 600 alumnos, para que la muestra sea representativa, lo mejor seria conocer
cuántos alumnos de cada curso hay: 200 alumnos de 3º, 150 de 4º, 150 de 1º de
Bachillerato y 100 de 2º de Bachillerato.
Como de 600 en total hemos de elegir a 20, de 200 de 3º hemos de elegir x:
20/600 = x/200 → x = 4000/600 =6.6 ≈ 7 alumnos de 3º

14. De igual manera podemos calcular los alumnos correspondientes a los demás
cursos:
20/600 = y/150 → y = 3000/600 = 5 alumnos de 4º
20/600 = z/150 → z = 3000/600 = 5 alumnos de 1º de bachillerato
20/600 = t/100 → t = 2000/600 =3.3 alumnos de 2º de bachillerato
De modo que en nuestra muestra de 20 alumnos; 7 son de 3º, 5 de 4 º, 5 de 1 º y 3 de
2 º.
Para la elección de cada alumno dentro de cada curso, utilizamos el muestreo
aleatorio simple.

15. d) Muestreo por conglomerados:
Aquí, en lugar de elegir individuos directamente, se eligen unidades más amplias
donde se clasifican los elementos de la población, llamados conglomerados.
Los conglomerados deben ser tan heterogéneos como la población a estudiar, para
que la represente bien.
No debemos confundir estrato y conglomerado. Un estrato es homogéneo (sus
elementos tienen las mismas características), mientras que un conglomerado
es heterogéneo (debe representar bien a la población).

16. Ejemplo:
Supongamos que queremos extraer una muestra aleatoria de los estudiantes
universitarios del país. Se necesitaria una lista con todos ellos para poder realizar
algún muestreo del tipo de los 3 anteriores, lo cual es muy dificil de conseguir.
Sin embargo, los estudiantes están clasificados por Universidades, Facultades y
Clases. Podemos seleccionar en una primera etapa algunas Universidades,
después algunas facultades al azar, dentro de las facultades algunas clases y
dentro de las clases, algunos estudiantes por muestreo aleatorio simple.
Los conglomerados en cada etapa serían las diferentes Universidades, las
diferentes facultades y los diferentes clases.

17. Ejercicio 1…
En una población de 1500 jóvenes, 7500 adultos y 1000 ancianos, se hace una
encuesta a 200 personas para conocer sus actividades de ocio preferidas. Si se
utiliza un muestreo estratificado, ¿que tamaño muestral corresponde a cada
estrato?.

18. Ejercicio 2…
Suponga que estamos investigando sobre el porcentaje de alumnos que trabajan
de una población de 20 alumnos de la universidad de talca.

19. Elija una muestra aleatoria simple de tamaño muestral de tamaño n=8 de esta
población.

20. Estimación
Una estimación estadística es un proceso mediante el cual establecemos qué
valor debe tener un parámetro según deducciones que realizamos a partir de
estadísticos. En otras palabras, estimar es establecer conclusiones sobre
características poblacionales a partir de resultados muestrales.
La estimación se divide en:
Estimación puntual
Estimación de intervalos de confianza

21. Estimación Puntual
Estimación mediante un solo valor de los parametros de una distribución.
La estimación puntual consiste en utilizar el valor de un estadístico para inferir el
par´ametro de una población.
❖Usamos la media muestral X¯ para estimar la media de una población µ.
❖Usamos la proporción de una muestra ˆp para estimar la proporción
poblacional p.

22. Propiedades deseables de los estimadores puntuales
Básicamente para que un estimador sea bueno, se desea que la varianza del
estimador sea lo más pequeña posible, mientras que la distribución de muestreo
debe concentrarse alrededor del valor del parámetro.
Estimadores Insesgados (Centrados): Se dice que la estadística = H(X 1, X 2,..., X
n ) es un estimador insesgado del parámetro, si. Es decir, si los valores del
estimador se centran alrededor del parámetro en cuestión.

23. Estimadores Consistentes: Si un estimador es consistente, converge en
probabilidad al valor del parámetro que está intentando
estimar conforme el tamaño de la muestra crece. Esto
implica que la varianza de un estimador consistente
disminuye conforme n crece.
Estimadores Eficientes (Insesgados de Varianza Mínima): El hecho de que un
estimador sea centrado no garantiza que sus realizaciones caigan cerca del valor
del parámetro, hace falta además que tenga la varianza pequeña.

24. La varianza de un estimador insesgado es la cantidad más
importante para decidir qué tan bueno es el estimador
para estimar el parámetro.
Estimación de la Media Poblacional: La media muestral es un estimador centrado
y consistente de la media poblacional. Este resultado es válido sin importar la
distribución de probabilidad de la población de interés, siempre y cuando la
varianza tenga un valor finito.

25. Estimación puntual Estimación de la Proporción: Tenemos una población dividida
en dos subconjuntos, en función de una característica determinada, de forma que
la proporción de la población que posee la característica es p, y la de los que no la
poseen es 1-p. Tratamos de estimar el valor de p. El estadístico dado por la
expresión siguiente, es un estimador centrado y consistente de la proporción
poblacional.
Estimación de la Varianza Poblacional: Cuando se desconoce la media poblacional,
debemos sustituir este parámetro por su estimador muestral, y el estimador a usar para la
varianza poblacional, que es centrado o insesgado sin importar cuál sea la distribución de la
población de interés, es la cuasivarianza muestral S^(2).

26. Ejemplo:
Se han anotado las calificaciones de los exámenes de recuperación de
matemáticas de los alumnos de un colegio. Las notas de 15 de ellos son: 4.8, 5.3,
6.2, 3.1, 5.4, 7.2, 8.4, 6.5, 7, 7.2, 0.5, 5.2, 6.8, 7.8, 4.2;
Además 9 de estos alumnos eran chicas. Determina un estimador puntual para:
A.La nota media de la población
B.La proporción de alumnas que se presentan a la recuperación.

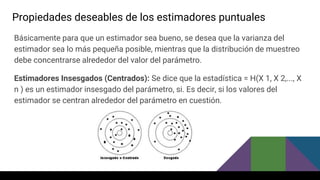
27. Estimación de la Varianza Poblacional:
Salario mensual y participación en el programa de adiestramiento para
una muestra aleatoria simple de 6 personas.
Formula:
S^(2)= (6){[(320)^2]+[(420)^2]+[(428)^2]+[(430)^2]+[(380)^2]+[(510)^2]} - (320+420+428+430+380+510)^2
6(6-1)
S^(2)=(6)(102,400+176,400+183,184+184,900+144,400+260,100) - (2,488)^2
6(5)
S^(2)=(6,308,304) - (6,190,144)
30
S^(2)=118,160
30
S^(2)=3,938.6666