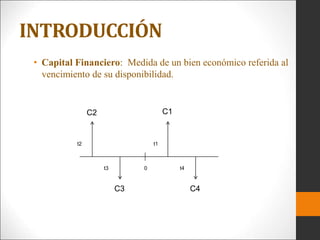
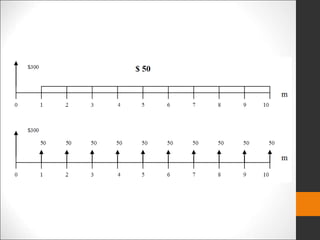
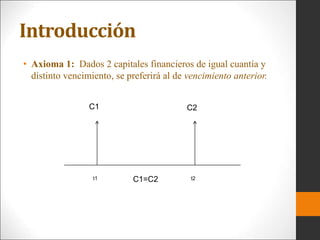
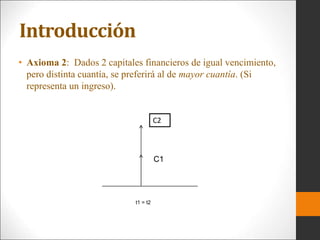
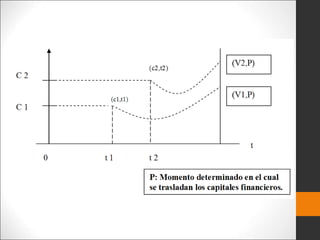
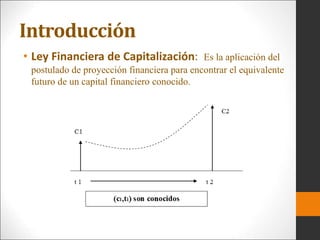
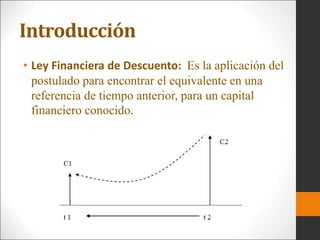
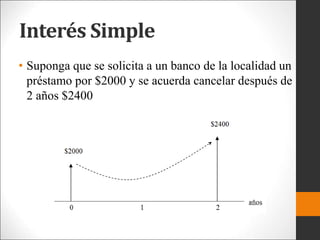
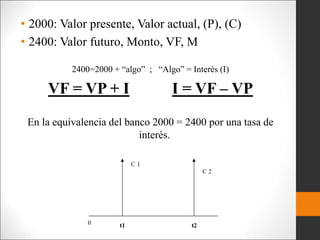
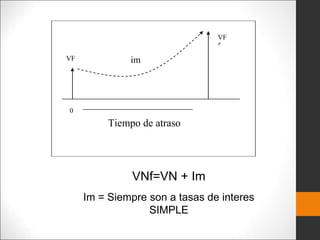
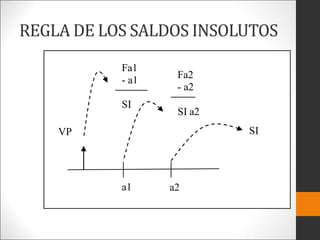
Este documento introduce los conceptos básicos de ingeniería económica. Explica que la ingeniería económica determina los factores y criterios económicos para seleccionar entre alternativas utilizando técnicas matemáticas. Estas técnicas ayudan a evaluar aspectos económicos de diferentes métodos para lograr un objetivo y a tomar decisiones financieras. También presenta algunas medidas comunes del valor como valor presente, valor futuro y tasa de retorno.

1. Ingeniería Económica I
Manuel Cepeda Alarcon
FACULTAD DE ECONOMÍA Y NEGOCIOS
ESPOL

2. • La ingeniería económica, en forma bastante simple, hace
referencia a la determinación de los factores y criterios
económicos utilizados cuando se considera una selección entre
una o más alternativas.
• Otra definición de la ingeniería económica plantea que es una
colección de técnicas matemáticas que simplifican las
comparaciones económicas.
INTRODUCCIÓN

3. • Con estas técnicas, es posible desarrollar un enfoque racional y
significativo para evaluar los aspectos económicos de los
diferentes métodos (alternativas) empleados en el logro de un
objetivo determinado.
• Funcionan igualmente bien para un individuo o para una
corporación que se enfrenta con una decisión de tipo
económico.
• Las técnicas y los modelos de ingeniería económica ayudan a
la gente a tomar decisiones.
• El marco de tiempo de la ingeniería económica es
generalmente el futuro.
INTRODUCCIÓN

4. • Las técnicas generan valores numéricos denominadas medidas
de valor, que consideran inherentemente el valor del dinero en
el tiempo. Algunas medidas comunes del valor son:
• Valor presente (VP)
• Valor futuro (VF)
• Valor anual (VA)
• Tasa de retorno (TR)
• Razón beneficio/costo (BK)
• Costo capitalizado (CC)
• En todos estos casos se considera el hecho de que el dinero hoy
vaIe una suma diferente en el futuro.
INTRODUCCIÓN

5. INTRODUCCIÓN
• Capital Financiero: Medida de un bien económico referida al
vencimiento de su disponibilidad.
C2
C4
C1
C3
t2
t4
t3
t1
0

6. Introducción
• Representar en un diagrama de valor tiempo o diagrama de flujo de
efectivo la operación de adquirir una refrigeradora hoy, pagando
$300 de entrada, “enganche” o de contado, y posteriormente 10
pagos de $50 cada fin de mes.

8. Introducción
• Axioma 1: Dados 2 capitales financieros de igual cuantía y
distinto vencimiento, se preferirá al de vencimiento anterior.
C1 C2
t2
t1 C1=C2

9. Introducción
• Axioma 2: Dados 2 capitales financieros de igual vencimiento,
pero distinta cuantía, se preferirá al de mayor cuantía. (Si
representa un ingreso).
C1
C2
t1 = t2

10. Introducción
• ATENCIÓN: No se debe manipular algebraicamente (sumar y/o
restar) capitales financiero, que tengan distintos vencimientos.
Si yo tengo $50 y voy a recibir $100 al final de mes, esto no
significa que tengo $150

11. Introducción
• Postulado de proyección financiera: Todo agente económico
dispone de un criterio referido al momento “P”, tal que por la simple
aplicación de ese criterio para todo capital financiero (c,t) existe otro
capital financiero (V,P) de manera que (c,t)=(V,P)

13. Introducción
• Si quisiera saber el costo de $500 de un TV hace 5 meses o después
de 5 meses, debemos aplicar el postulado de proyecciones
financiera.
• El postulado de Proyección financiera se traduce operacionalmente
en Leyes financieras.

14. Introducción
• Ley Financiera de Capitalización: Es la aplicación del
postulado de proyección financiera para encontrar el equivalente
futuro de un capital financiero conocido.

15. Introducción
• Ley Financiera de Descuento: Es la aplicación del
postulado para encontrar el equivalente en una
referencia de tiempo anterior, para un capital
financiero conocido.

16. Interés Simple
Capitulo I

17. Interés Simple
• Suponga que se solicita a un banco de la localidad un
préstamo por $2000 y se acuerda cancelar después de
2 años $2400

18. • 2000: Valor presente, Valor actual, (P), (C)
• 2400: Valor futuro, Monto, VF, M
2400=2000 + “algo” ; “Algo” = Interés (I)
VF = VP + I I = VF – VP
En la equivalencia del banco 2000 = 2400 por una tasa de
interés.

19. • Tasa de interés efectivo: Es el factor mediante el cual el presente
se convierte en futuro durante un periodo determinado. Se la
expresa de 2 formas:
1. Forma Porcentual: Se utiliza en lenguaje formal, escrito y se
debe incluir el tiempo del cual actúa. i = 10% anual; i = 2%
mensual.
2. Forma Matemática: Se la utiliza dentro de las fórmulas y se
obtiene dividiendo para 100. i = 0,1; i = 0,02

20. • La tasa de interés también refleja la relación que existe entre el
interés y el valor presente en un período.
Las unidades de i y t deben ser las mismas:
i = anual ; t = años
i = mensual ; t = años
(1 + it ) : Factor de acumulación de capital a interés simple.

21. Tiempo Real
1 mes 28,29,30,31 días.
1 año 365, 366 días.
1 año 52 semanas.
1 semana 7 días.
Tiempo Comercial
1 mes 30 días.
1 año 360 días.
1 año 48 semanas.
1 semana 7 días.

22. FORMULAS
•VF = VP( 1+ it )
•M = C ( 1 + it )
• VP = VF (1 + it)-1
• C = M / ( 1 + it)

23. Ejercicio 1
• Una persona participa en un cuadro financiero y le toca cobrar
el 18vo mes. Si dentro de 18 meses recibirá $ 3000. Cuál será
el valor equivalente que recibiría si le hubiese tocado cobrar en
el 5to mes?
Asuma i = 12.5% anual

24. Ejercicio 2
• El Ing. González recibió por parte de un deudor 3 alternativas
para cancelar una deuda:
1.- Cancelar $2000 hoy y $2500 dentro de 6 meses.
2.- Cancelar $6000 dentro de 1 año.
3.- Cancelar durante 1 año cada final de trimestre $1500.
¿Cuál alternativa es más conveniente para el Ing. González si
la tasa simple es del 10% anual?
(F.F) = hoy

25. Ejercicio 3
• La señora Cordero hace un préstamo para ampliar su
negocio de $5300 cobrándole una tasa del 5%
trimestral simple y combina para pagar dentro de 1
año 4 meses.
1.- Cuál es el valor que tendrá que pagar la señora
Cordero al cabo de ese tiempo?
2.- Si la señora no paga en esa fecha y se atrasa 8 días,
la financiera le cobra el 3% mensual de interés por
mora. ¿Cuál fue el valor que pagó atrasado la señora
Cordero?

26. INTERÉS DE MORA
• Pago después de la fecha de vencimiento: Cuando una obligación
no es cancelada en la fecha señalada para su vencimiento,
comienza a ganar intereses llamados por “mora”, los cuales se
calculan en base al valor nominal por el tiempo en que se atrasó el
pago, a una tasa de interés fijada con anterioridad.

27. VF
0
VF
f
Tiempo de atraso
im
VNf=VN + Im
Im = Siempre son a tasas de interes
SIMPLE

28. ECUACIONES EQUIVALENTES
• Una ecuación de equivalencia se forma cuando
se tiene distintas obligaciones en diferentes
fechas. Para poder formar la ecuación de
equivalencia se escoge una denominada fecha
focal.
• La fijación de esta debe corresponder
estrictamente a lo prestado en los pagarés u
obligaciones en la cual se llevan todas éstas y los
pagos a una tasa denominada tasa de costo de
dinero.

29. ECUACIONES EQUIVALENTES
• En el cual se realizan la sumatoria del
flujo de deudas en la fecha focal y se
iguala a la sumatoria de pagos en fecha
focal. Esta igualdad permite encontrar
algún dato desconocido que puede ser
deuda o pago.
∑ DEUDAS = ∑ PAGOS

30. Ejercicio 4
• Una persona en cierta fecha firma un pagaré por
$12000 a 90 días al 8%. 30 días después firma
otro pagaré por $10000 a 90 días sin intereses. 60
días después de la primera fecha conviene pagar
a su acreedor $4000 y hacer un solo pago por un
valor que cancela la deuda 120 días contados
desde la última fecha. Consideré un rendimiento
del dinero del 9% y determine el valor del pago
único.

31. Ejercicio 5
• El señor Gómez hace un préstamo el 14 de Julio $3500 a 5
meses y medio al 40% interés simple. También hace otro
préstamo después de $2000 con el 54% de interés simple y
vencimiento a 3 meses. Si considera para la equivalencia una
tasa del 55% y se desea liquidar sus deudas con 2 pagos
iguales dentro de 8 y 12 meses respectivamente. (Fecha focal
el 6 mes).

32. Ejercicio 6
• Una persona contrajo una deuda hace 8 meses por $2000 con
el 40% de i simple y que vence dentro de 4 meses, debe pagar
otra de $1500 realizada hace 2 meses con el 35% de i simple y
que vence de dos meses. Con una tasa del 42%, que pago
debería hacer hoy para saldar sus deudas si se compromete a
pagar $1000 dentro de 6 meses.

33. PAGOS PARCIALES O ABONOS
• Para el tratamiento de obligaciones o
documentos que permiten pagos parciales o
abonos dentro del plazo de la deuda, en lugar de
realizar un solo pago en la fecha de vencimiento,
existen diferentes criterios, de los cuales
analizaremos los 2 más importantes.

34. PAGOS PARCIALES O ABONOS
• Regla Comercial: Los valores futuros de la obligación y de los
diferentes abonos, deben calcularse por separado en la fecha
de vencimiento.
El valor por cancelar en esa fecha (saldo deudor o insoluto) es
la diferencia entre el valor futuro de la obligación y la
sumatoria del valor futuro de los abonos.

35. REGLA COMERCIAL
VP
VF
t
a1 a2 an
Fa1
Fa2
Fan
∑
SI = VF - ∑
SI = VF - ∑(Fa1 + Fa2 + …… + Fan)

36. PAGOS PARCIALES O ABONOS
• Regla de Saldos Insolutos: Cada vez que se realiza un abono
debe calcularse el valor futuro de la deuda hasta esa fecha y
restar a esa cantidad el valor del abono, obteniéndose de esta
forma el saldo insoluto a la fecha del abono.
Se repite el procedimiento para todos los abonos sucesivos,
hasta obtener el saldo insoluto en la fecha de vencimiento.

37. REGLA DE LOS SALDOS INSOLUTOS
Fa1
- a1
SI
a1
VP
a1 a2
Fa2
- a2
SI a2
SI

38. CONCLUSION
• El saldo deudor por la regla de saldos insolutos siempre será
mayor que el calculado por la regla comercial, debido a que el
primer método se calculan intereses sobre intereses, es decir
se aplica la fórmula de interés simple más de una vez a un
mismo capital financiero.

39. Ejercicio 7
• Para una obligación de $10000 a un año plazo con intereses
del 12%, el deudor realiza los siguientes abonos:
$5000 a los 3 meses y $4000 a los 8 meses.
Calcular aplicando la regla comercial y de saldos insolutos al
deudor en la fecha de vencimiento.