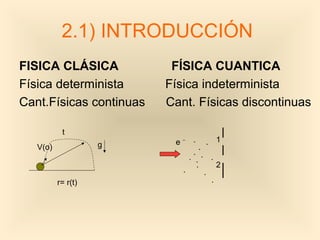
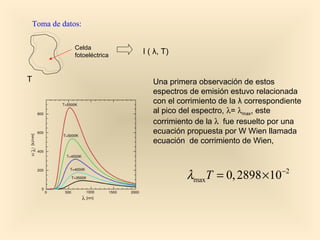
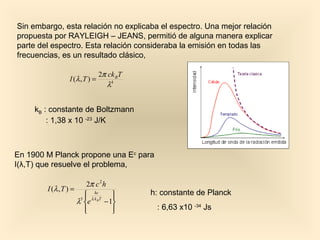
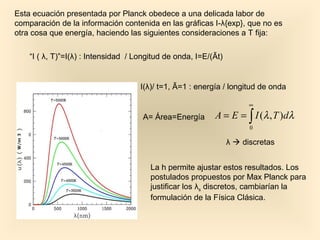
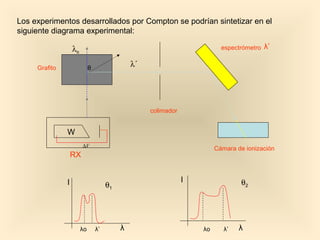
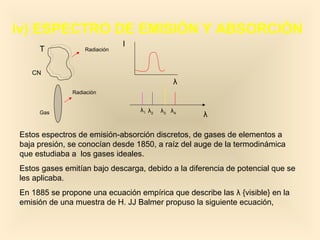
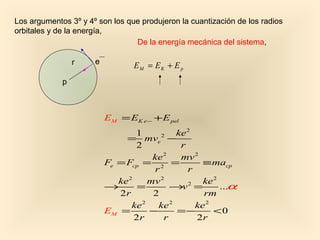
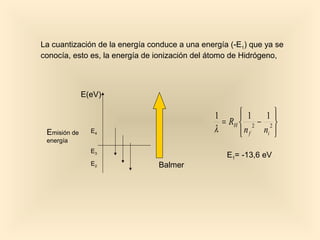
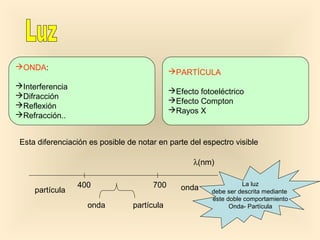
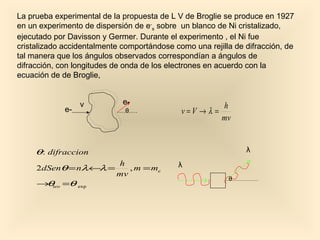
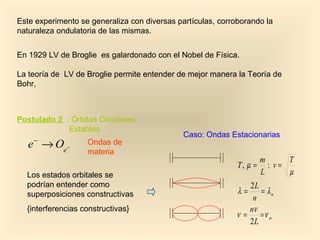
Este documento introduce conceptos fundamentales de la mecánica cuántica a través de fenómenos observados a finales del siglo XIX que no podían explicarse con la física clásica, como la radiación del cuerpo negro y el efecto fotoeléctrico. Explica cómo Planck, Einstein, Compton y otros desarrollaron nuevos modelos y teorías cuánticas para dar cuenta de estos fenómenos. También presenta el modelo atómico de Bohr, que introdujo la cuantización para explicar los espectros ató

1. 2) INTRODUCCIÓN A LA
MECÁNICA CUANTICA

2. 2.1) INTRODUCCIÓN
FISICA CLÁSICA FÍSICA CUANTICA
Física determinista Física indeterminista
Cant.Físicas continuas Cant. Físicas discontinuas
t
e . . 1
V(o) g .
. .
. . .
. 2
. .
r= r(t) .

3. En el último tercio del s. XIX:
• Radiación de cuerpo negro
• Efecto fotoeléctrico
• Efecto Compton
• Espectros de Absorción- Emisión
• Emisión de RX
• Estabilidad de la materia …

4. 2.2) FENÓMENOS ANTECEDENTES
i) RADIACION DE CUERPO NEGRO
Este fenómeno presentado por G R Kirchhoff en 1862 no pudo ser resuelto
clásicamente hasta que en 1900 M Planck, usando argumentos
revolucionarios, lo resuelve.
El cuerpo negro, CN, es un modelo que representa a un cuerpo {sistema}
de absorción infinita. Un buen ejemplo es una cavidad con abertura
pequeña.
Todo cuerpo radia energía en función de su
temperatura, esto permitió analizar al CN en
Cavidad=CN
cuanto a su emisión para diversas
temperaturas. La información experimental se
T conocía con mucha anticipación debido a que
era un viejo problema sin resolver.

5. Toma de datos:
Celda
fotoeléctrica
I ( λ, T)
T Una primera observación de estos
espectros de emisión estuvo relacionada
con el corrimiento de la λ correspondiente
al pico del espectro, λ= λmax, este
corrimiento de la λ fue resuelto por una
ecuación propuesta por W Wien llamada
ecuación de corrimiento de Wien,
λmaxT = 0, 2898 ×10−2

6. Sin embargo, esta relación no explicaba el espectro. Una mejor relación
propuesta por RAYLEIGH – JEANS, permitió de alguna manera explicar
parte del espectro. Esta relación consideraba la emisión en todas las
frecuencias, es un resultado clásico,
2π ck BT
I (λ , T ) =
λ4
kB : constante de Boltzmann
: 1,38 x 10 -23 J/K
En 1900 M Planck propone una Ec para
I(λ,T) que resuelve el problema,
2π c 2 h
I (λ , T ) =
 hc  h: constante de Planck
5  λ k BT 
λ e − 1

 
 : 6,63 x10 -34 Js

7. Esta ecuación presentada por Planck obedece a una delicada labor de
comparación de la información contenida en las gráficas I-λ{exp}, que no es
otra cosa que energía, haciendo las siguientes consideraciones a T fija:
“I ( λ, T)”=I(λ) : Intensidad / Longitud de onda, I=E/(Ãt)
I(λ)/ t=1, Ã=1 : energía / longitud de onda
∞
A= Área=Energía A = E = ∫ I ( λ , T ) dλ
0
λ  discretas
La h permite ajustar estos resultados. Los
postulados propuestos por Max Planck para
justificar los λs discretos, cambiarían la
formulación de la Física Clásica.

8. POSTULADOS
1) Los estados energéticos moleculares son
discretos según la siguiente ecuación,
En = n h ν n: entero, ν: frecuencia lineal
Max Planck
2) La emisión o absorción molecular se produce solo 1858(Kiel)-
cuando la molécula cambia de estado, el cual es 1947(Gotinga)
caracterizado por n, numero cuántico energético,
nf ←→ ni

9. ii) EFECTO FOTOELÉCTRICO
Este efecto fue reportado por H Hertz en 1887,
cuando investigaba en el laboratorio la producción de
las OEM.
Este fenómeno fue resuelto por A Einstein y Heinrich Hertz
presentado en 1905 en su reconocido año milagroso. 1857(Hanburgo)-
1894(Bonn)
UV
es : La física clásica no resolvía el
fotoelectrones problema puesto que, por ejemplo, la
radiación fotoelectrónica se debía
Superficie producir luego de varios minutos de
metálica “iluminar” la superficie , sin embargo
la emisión es casi instantánea.

10. clásica cuántica
γ
e
Albert Einstein
Energía localizada 1879(Ulm)-
Energía en el fotón, γ 1955(Princenton)
dispersada en
toda la λ
Albert Einstein propone a la luz compuesta por partículas o fotones (γ), esto
es, le otorga una concepción cuántica, lo cual permite explicar los
resultados experimentales.

11. Montaje
experimental
UV sencillo: Luz:I,ν
es : fotoelectrones v
Intensidad I Ek  Ek,max e-
A
Superficie V
metálica
∆V = V
Asumiendo conservación de la energía,
Eγ = Ee − = E k ,max + φ
Ek ,max = hv − φ...(ε )
v : frecuencia del fotón
φ : función trabajo que caracteriza al metal

12. Los resultados experimentales se muestran a continuación, en i)
la relación lineal entre Ek,max-ν muestra la frecuencia umbral o de
corte y en la pendiente el valor de h, en ii) que la intensidad no
influye la Ek,max y la iii) mientras mas energético el fotón el e-
adquiere mayor Ek,max.
Ek,max
i)
νc = νu ν
φ
νc = νu :
Frecuencia
de corte o ν
umbral
tgθ = m = h

13. ii) I =i I 2 ,ν iii) I =i
I 2 = I 1 ,υ 2 > υ 1
I2>I1
I 1 ,ν
Vs = V f ∆V = V ∆V = V
VS 2 VS1
Ek , max = Eγ − e − = q∆V = eVs
VS = V f : potencial de frenado
EK,MAX
+ -
∆V = Vs
Ek ,max = eVS

14. iii) EFECTO COMPTON
Efecto descrito en 1923 por A H Compton, donde se
informa acerca de la dispersión de γs RX por un blanco
de grafito.
La teoría clásica indica que la dispersión estaría
dependiendo tanto de la intensidad de radiación así
A H Compton
como del tiempo de exposición, lo cual es desbaratado
por el experimento. 1892(Ohio)-
1962(Berkeley)
Recordando que la teoría clásica indica que la
radiación θ
emisión {dispersión} es producida por oscilación de
e-s, el proceso se representaba de la siguiente
forma,
sustancia
λ’
λ
θ
e-

15. Sin embargo, A Compton describe el proceso en una imagen moderna de la
radiación, esto es, mediante fotones {A Einstein}, en la cual se producen
“choques” entre fotones RX y e-,
A Compton resuelve el
e-
λ0 problema mediante la teoría de
Φ choques relativistas ,
θ proponiendo la siguiente
ecuación,
λ’
λ '−λ0 = ∆λ = λC (1 − cos θ )
λ c : longitud de onda de Compton
h
λC = ≈ 0,00243 ×10 −9 , m = me−
mc ∆ λ : corrimiento de Compton
λ0 : λ a dispersión “cero”

16. Los experimentos desarrollados por Compton se podrían sintetizar en el
siguiente diagrama experimental:
λo espectrómetro λ’
Grafito θ
λ´
colimador
W
∆V
Cámara de ionización
RX
I I θ2
θ1
λo λ’ λ λo λ’ λ

17. λ’: Espectrómetro de cristal giratorio
I : I registrada en la cámara de ionización
P
λ´ λ´
α α
Estructura de Red
Cristalina
P :maximo
2dSenα = nλ
Esta extensión de los fotones de luz { A Einstein} a fotones del espectro
EM , γEM , {A Compton} , permite intensificar los marcos conceptuales que
se producirían entre 1925-26 , para formalizar la Física Cuántica, esto es,
los formalismos de Heisenberg y Schroedinger.

18. iv) ESPECTRO DE EMISIÓN Y ABSORCIÓN
I
T Radiación
CN
λ
Radiación
Gas λ1 λ2 λ3 λ4
λ
Estos espectros de emisión-absorción discretos, de gases de elementos a
baja presión, se conocían desde 1850, a raíz del auge de la termodinámica
que estudiaba a los gases ideales.
Estos gases emitían bajo descarga, debido a la diferencia de potencial que se
les aplicaba.
En 1885 se propone una ecuación empírica que describe las λ {visible} en la
emisión de una muestra de H. JJ Balmer propuso la siguiente ecuación,

19. Serie de 1 1 1
= RH  2 − 2  ; n= 3,4,… Visible y UV
Balmer λ 2 n 
RH: constante de Rydberg, RH = 1,0973732 * 107
Espectros de absorción y emisión del Hidrógeno
λ

20. Posteriormente, en base a este reporte, se proponen otras ecuaciones
que justifican diversas series en los espectros de emisión del H,
Serie de 1 1 1 ; n= 2,3,4,… UV
= RH  2 − 2 
Lyman λ 1 n 
Serie de 1 1 1
= RH  2 − 2  ; n= 4,5,… IR
Paschen λ 3 n 
1 1 1
Serie de = RH  2 − 2  ; n= 5,6,… IR
Brackett λ 4 n 

21. La importancia de estos espectros radica en que son propios de cada
elemento, tanto en su versión de emisión como de absorción,
λ

22. La técnica espectroscópica de absorción permite identificar la composición
tanto cualitativa como cuantitativa de las sustancias o materia en general,

23. 2.3) Modelo de Bohr
Explicación empírica:
ESPECTROS
* Series de Lyman,
ATÓMICOS
Balmer, Paschen y
Brackett
N Bohr
1885-1962
1  1
 1
= RH  2 − 2  (Copenhague)
λ  n f ni 
 
En 1913, Niels Bohr propone un modelo de átomo de H, en función a
estos resultados así como por el conocimiento de ciertos valores físicos
ya determinados, por ejemplo, la energía de ionización del H,
E ionización aproximadamente 13,6 eV

24. La teoría de Bohr propone un modelo semiclásico del átomo de H,
basado en 4 postulados:
1.- El e- orbita al p+ circularmente debido a la fuerza eléctrica ( clásico)
2.- Estas órbitas electrónicas son estables, esto es, el e- no radía
energía (no clásico)
3.-La radiación de energía del e- sólo se produce cuando cambia de
órbita( cuántico)
4.-Las órbitas electrónicas cumplen la cuantización del momento
angular (L)(cuántico)
L = mrv , L = r × p = mr × v
→ L = mrv = nh
L = mrv = nh : n = 1, 2, 3....
h
h=
2π
→ cuántica

25. Los argumentos 3º y 4º son los que produjeron la cuantización de los radios
orbitales y de la energía,
De la energía mecánica del sistema,
r e EM = EK + E p
p
EM = EK e − + E pel
1 ke 2
= mve − 2
2 r
ke 2 mv 2
Fe = Fcp = 2 = ≡ macp
r r
ke 2 mv 2 ke 2
→ = →v =2
...α
2r 2 rm
ke 2 ke 2 ke 2
EM = − =− <0
2r r 2r

26. FI : Tierra - Sol
rn rm E<0
De la condición de cuantización de L,
L = mrv = nh...β
ke 2 
α : v2 = 
mr  ke 2 n2h2  h2  2
2 = 2 2 → r ( n) =  2 
n = r0 n 2
 nh   mr m r  mke 
β : =v
 mr  

°
→ r ( n = 1) = r0 = 0, 53 Α, radio de Bohr

27. Si esta r(n) se reemplaza en la ecuación de energía, se obtienen los E = E(n),
ke 2 1  mk 2 e 4  1
E ( n) = − × 2 2 ≡ − 2 
× 2
2 h n  2h  n
mke 2
E1
E ( n) = E1 = − ,6 eV
13
n2
 mk 2e 4  mk 2e 4 MF 2L4L2 ML2
¿ Energía − 2 ? = 2 2 2
= 2
 2h  h J T T
( Ke )
2
2
F 2L4

28. La cuantización de la energía conduce a una energía (-E1) que ya se
conocía, esto es, la energía de ionización del átomo de Hidrógeno,
E(eV)
1  1
 1
= RH  2 − 2 
Emisión de E4 λ  n f ni 
 
energía
E3
E1= -13,6 eV
E2 Balmer

29. Para la comprobación de las ecuaciones de las series se usa el
postulado 3º,
E1
E ( n) =
n2
c
Ei − E f = Eγ ≡ hν ≡ h
λ
1
 1  hc

Ei − E f = E1  2 − 2  =
ni
 nf  λ

1 E1  1
 1 
 E1
=  2 − 2 , =RH =1, 0973732 ×107 m −1
λ hc n f
 ni 
 hc
1  1
 1 

= RH  2 − 2 
λ n f
 ni 


30. Las series ahora son entendidas como producidas por las
transiciones electrónicas, entre los diversos niveles de energía, tal
como se muestra en la figura,

31. Bohr extiende su modelo del H a átomos tipo H (hidrogenoides) , He+ , Li ++,
caracterizados por sus Z,
n 2 ro
r (n) = n 2 ro → r * (n) =
Z
E1 E1Z 2
E ( n) = 2 → E * ( n) = 2
n n

32. 2.4) Naturaleza dual de la luz
: …un interesante problema sin resolver
Griegos: divinidad
Galileo: medición descrita en SSS ( Salviati-
Sagredo-Simplicio)
Newton : haz de partículas
Fizeau : 1ra medición no astronómica, v~c
Maxwell : onda v = c =3*10 8
Einstein : fotones de luz
Nosotros {actualidad} : onda- partícula
¿? Misterio acerca del mejor
modelo para describirla

33. ONDA:
PARTÍCULA
Interferencia
Efecto fotoeléctrico
Difracción
Efecto Compton
Reflexión
Rayos X
Refracción..
Esta diferenciación es posible de notar en parte del espectro visible
λ(nm)
400 700 onda
La luz
partícula debe ser descrita mediante
este doble comportamiento
onda partícula Onda- Partícula

34. Principio de complementaridad de N Bohr
Luz  { ONDA} +{ PARTÍCULA}

35. 2.5) La naturaleza ondulatoria de
las partículas
Simetría : Onda  Partícula
Albert Einstein Louis Víctor de Broglie
Propone, aproximadamente en 1923, que las partículas de
Louis Víctor de
materia tienen comportamiento ondulatorio. Lo cual
Broglie
establece el comportamiento simétrico onda partícula de los
constituyentes del universo. 15 de agosto de
1892(Dieppe)-19
de marzo de
onda 1987(Paris)
Partícula

36. Partiendo de las ideas de M Planck, asociadas a los estados energéticos
vibracionales moleculares cuantizados y de A Einstein, de la energía
relativista del fotón( onda→particula) obtiene la longitud de onda asociada
a los electrones( particula→onda)
E = pc ¬ relatividad { AE}
E = hv ¬ cuántica {MP}
c c
pc ≡ hv → p ≡ pλ = h ¬ ν=
ν λ
h
λ=
p = mv
Esta λ de De Broglie es la λ de las llamadas Ondas de
Materia.

37. La prueba experimental de la propuesta de L V de Broglie se produce en 1927
en un experimento de dispersión de e-s sobre un blanco de Ni cristalizado,
ejecutado por Davisson y Germer. Durante el experimento , el Ni fue
cristalizado accidentalmente comportándose como una rejilla de difracción, de
tal manera que los ángulos observados correspondían a ángulos de
difracción, con longitudes de onda de los electrones en acuerdo con la
ecuación de de Broglie,
v e- h
e- θ v=V → λ =
mv
θ: difraccion λ
h λ
2dSenθ = nλ← =
λ , m = me
mv
θ
→ teo =θ exp
θ

38. Este experimento se generaliza con diversas partículas, corroborando la
naturaleza ondulatoria de las mismas.
En 1929 LV de Broglie es galardonado con el Nobel de Física.
La teoría de LV de Broglie permite entender de mejor manera la Teoría de
Bohr,
Postulado 2 : Órbitas Circulares
Estables
Caso: Ondas Estacionarias
−
e → Oe − Ondas de
materia
m T
T, µ = : v=
Los estados orbitales se L µ
podrían entender como 2L
superposiciones constructivas λ= = λn
n
{interferencias constructivas} nν
ν = =ν n
2L

39. Postulado 4 : Cuantización
del L
h
L = nh = n = mrv
2π
h
Orbitas : 2π r = λ n = n rn
p = mv
nh
2π r =
mv
→ L ≡ mrv = nh
 H : interferencias constructivas de Os e-s

40. Wilhelm Wien
13 de enero de 1864,
Fischhausen(Prusia)-30 de agosto de
1928(Munich)
Nobel de Física 1911: por las Leyes de
radiación de calor

41. Gustav Robert Kirchhoff
12 de marzo de 1824, Köningsberg(Prusia)-17 de
Octubre de 1887, Berlin
Investigacion: Tres Leyes de espectroscopia y
dos Leyes de electricidad

42. John William Strutt, tercer Barón de
Rayleigh
12 de noviembre de 1842(Essex)- 30 de
junio de 1919(Essex)
Nobel de Fisica en 1904:por
descubrimiento del argon y densidad de
muchos gases

43. Sir James Hopwood Jeans
11 de setiembre de 1877(Lancashire)-16 de
setiembre de 1946(Surrey)
Investigación: Radiación de CN, astronomía

44. Johann Jakob Balmer
1825 (Lausen)-1898(Basilea)
Investigación: Espectros de emisión de
gases, Ley empírica de emisión para el
H.

45. Clinton Joseph Davisson
22 de octubre de
1881(Bloomington)-1 de
febrero de
1958(Charlottesville)
Nobel de Física en 1937:
difracción de electrones por
cristales

46. Lester Halbert Germer
10 de octubre de 1896(Chicago)-10 de
marzo de 1971(New York)
Investigación: difracción de electrones en
cristales, termoiónica.