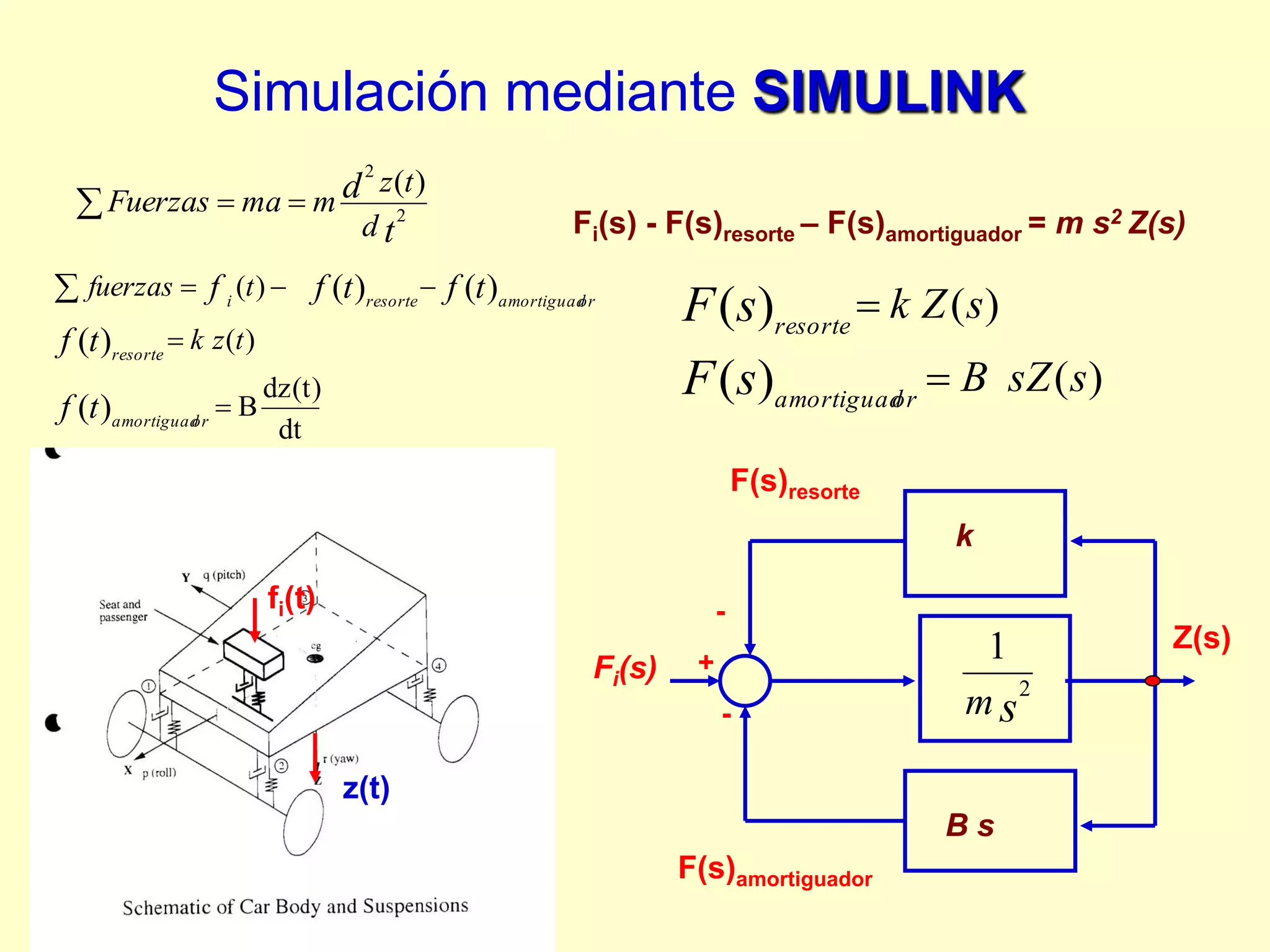
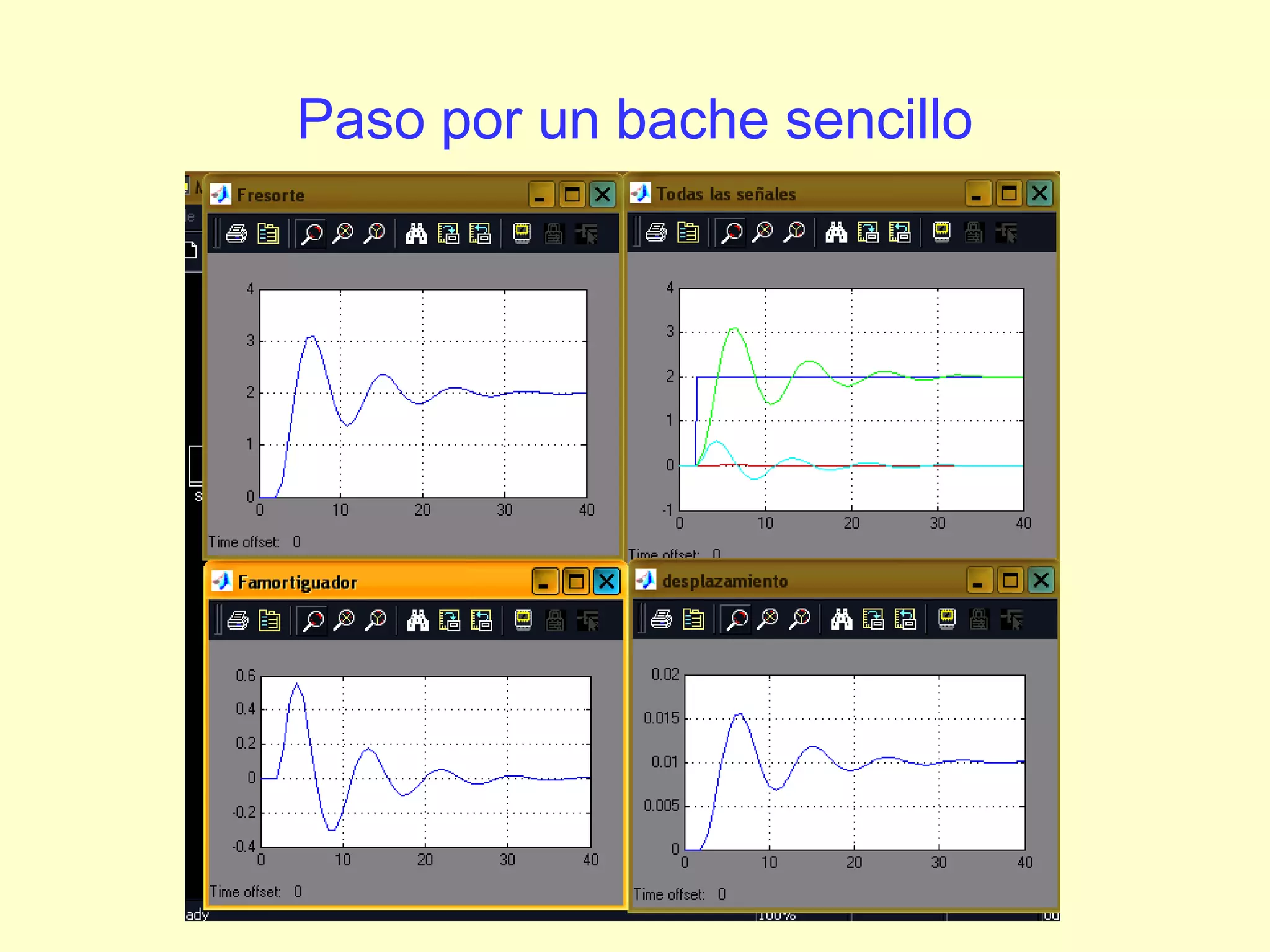
1) El documento describe el modelado y estudio de ecuaciones diferenciales lineales de primer orden utilizando la transformada de Laplace en MATLAB-SIMULINK. 2) Explica cómo modelar sistemas físicos como temperatura en un horno o llenado de un tanque mediante ecuaciones diferenciales. 3) Detalla el análisis de ecuaciones diferenciales lineales de primer orden a través de la obtención de las funciones de transferencia G(s) y respuesta Y(s).

1. “Modelación y Estudio de las
ecuaciones diferenciales l.c.c.c. en
el dominio de Laplace (frecuencia)
utilizando MATLAB-SIMULINK”
Maestro: Francisco Palomera Palacios
Departamento de Mecatrónica y Automatización,
ITESM, Campus Monterrey
fpalomera@itesm.mx

2. Motivación
• Análisis y estudio intuitivo (no formal) de las
ecuaciones diferenciales lineales c.c.c. a través
de la transformada de Laplace.
• Ilustrar el comportamiento de la respuesta de
sistemas físicos con la ayuda del programa
computacional MATLAB-SIMULINK.
El que haya personas interesadas en promover,
motivar y escuchar sobre el tema de ecuaciones
diferenciales y la Transformada de Laplace.

3. Modelación de Sistemas Dinámicos utilizando
Ecuaciones Diferenciales Ordinarias (EDO)
Sistema
Físico
Sistema (Físico)
a modelar
Función forzante
y(t)
u(t)
Respuesta del sistema
-Sistema Mecánico (sistema de suspensión en los autos)
- Sistema Hidráulico (llenado de un tanque)
- Sistema térmico (temperatura en un horno)
-Sistema Eléctrico (velocidad de motores)
- Sistema Fisiológico (efecto de una dosis en el cuerpo h. )
- Sistema Económico ( inflación)
- Sistema de producción (producción entre máquinas)
Relación causal

4. Para obtener una ecuación diferencial,
podemos utilizar:
• Leyes físicas: que de acuerdo a la naturaleza del sistema,
rigen la relación causal entre las variables de interés.
• Pruebas experimentales (análisis de la respuesta transitoria
del sistema ante una función forzante conocida).
• Por analogías de comportamientos entre sistemas que guardan
un comportamiento similar, a pesar de ser de naturaleza diferente.
• Aplicación de algoritmos y recursos computacionales para
procesar los datos obtenidos de pruebas experimentales.
…

5. Sistemas físico: Temperatura en un horno
Horno
Flujo de
Combustible:
qi(t)
Temperatura:
T(t)horno
Temperatura
Flujo de gas
Relación causal

6. Sistema Físico:Llenado de un tanque
qo(t): Caudal de salida
qi(t): Caudal de entrada
A:
área del tanque
p(t): señal que regula
el caudal hacia el tanque.
h(t): altura del tanque
Rh: resistencia Hidráulica
Tanque
Caudal de
entrada
qi(t)
Nivel: h(t);
Caudal de
Salida, qo(t)
Relación causal

7. Análisis de una ecuación diferencial
lineal c. c. c.
2
-3t
2
d y(t) dy(t)
+ 0.4 + 0.03 y(t) = 1.5 + Sen10t
dt
dt e
Sistema (Físico)
a modelar
u(t): Comportamiento deseado
La respuesta y(t) de un sistema
mecánico ante una función forzante
u(t) está definida por la ecuación
diferencial; y(0)= 2; y’(0) = 0
Función forzante
y(t)
u(t)
Respuesta del sistema
)
(
)
(
13
.
0
)
(
4
.
0
)
(
2
2
t
u
t
y
dt
t
dy
d
t
y
t
d 



8. Función forzante: u(t)
de
Fun ma
ción e gnitud
scalón 1.5;
multiplicada por
Función una expo
Senoid nen
al cial
-3t
= 1.5 + Sen
u(t) 10t
e

9. Analogía de Sistemas de Primer Orden
R
C
vi(t): fuente
de voltaje
i(t):
vo(t)
vi(t): fuente de voltaje
vo(t): voltaje de salida
C: Capacitor
R: Resistencia
qo(t): Caudal de salida
qi(t): Caudal de entrada
A:
área del tanque
p(t): señal que regula
el caudal hacia el tanque.
h(t): altura del tanque
Rh: resistencia Hidráulica
i
i
o
o
o
o
v (t)
v (t)
v (t)
v (
d
dt
d
dt
v (t
)
t) )
t
v (
R.C

 
 
dc(t)
+ c(t) = .
dt
τ K u(t) K: Ganancia en estado estable
: Constante de tiempo
qi(t)
0(t)
dq0(t)
q
dt
d
dt
qi(t)
+ q0(t) =
R.A

 q0(t) 

10. La transformada de Laplace en la
modelación, estudio y solución de
las ecuaciones diferenciales.

11. Relación entre f(t) y su equivalente F(s).
{ }
f(t)
L 0
-st
d
f(t) t
e


{ }
1
s 6
-6t
e 

L
f(t)
tiempo
j: Eje Imaginario
 : Eje real
F(s)
Plano Complejo: s =  + j
16 16
4 8
2
2
2 Se
{ }
s
t =
4
s
n
2

 
L
2
6s 9 6s
4 13
2
-3t 2 10 10
2 2 2
(s+3) s
Sen2t
5 =
s
{ } 5
e  
    

L
Ejemplos

12. Principales funciones a obtener de una
ecuación diferencial: G(s) y Y(s)
Y(s)
U(s)

c.i.=0
2)G(
s)
Al aplicar la Transformada de Laplace a una ecuación diferencial, dos
expresiones son de gran interés:
1) Y(S): La función respuesta de un sistema. (incluye las c.i. y a la
función forzante)
; Función de transferencia del sistema (considera c.i.=0 y
no se sustituye la función forzante.
n(s)
n(s) 0;ceros
K( K
K :ganancia
:
d
s a)...
;
(s b)(s (s)
d(s) 0;p
c)...
olos
(o)
: (X)






jw

x
o o x
x
Tanto G(s) como Y(s) estan formadas por los términos:

13. G(s) y Y(s)
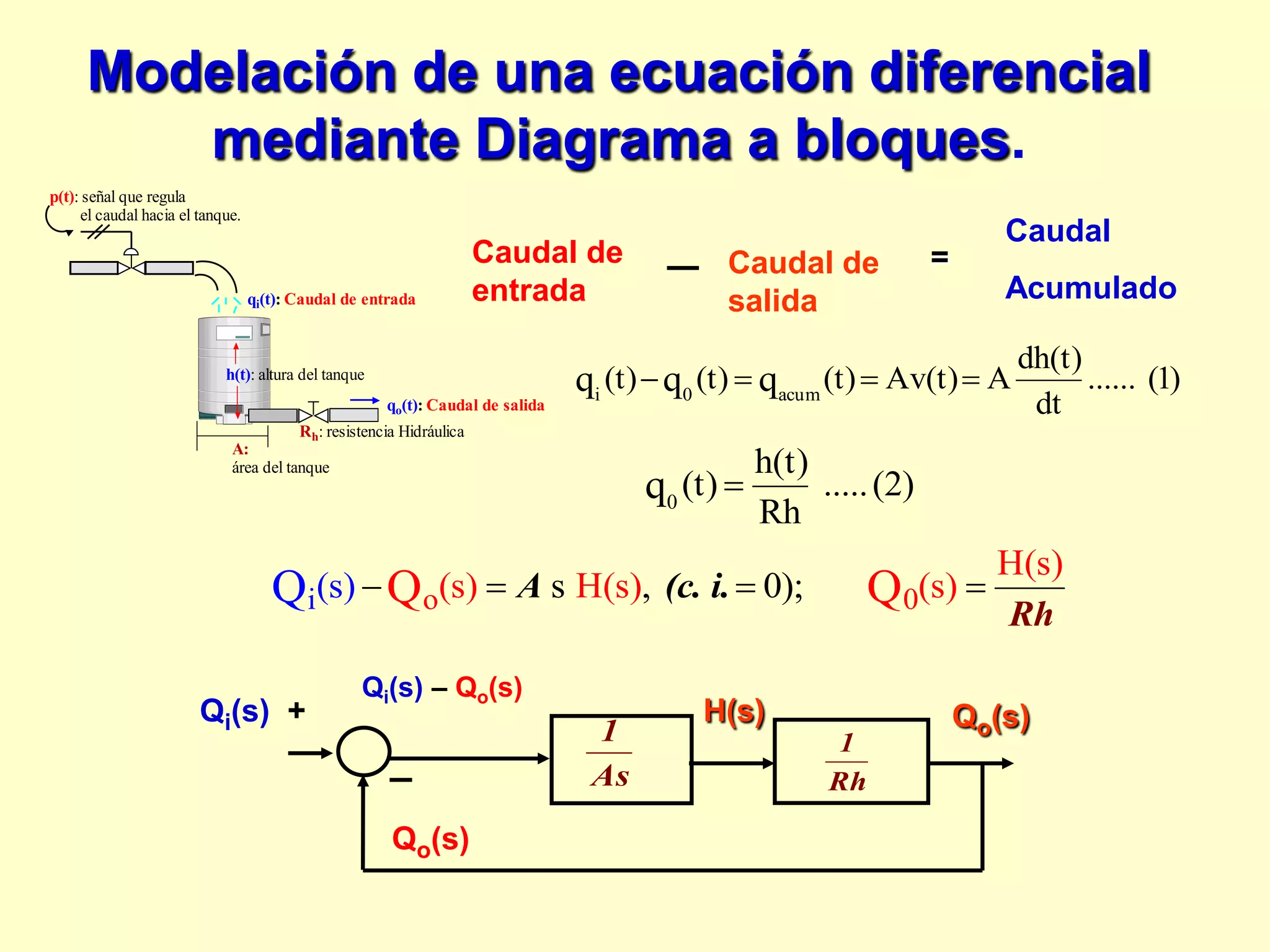
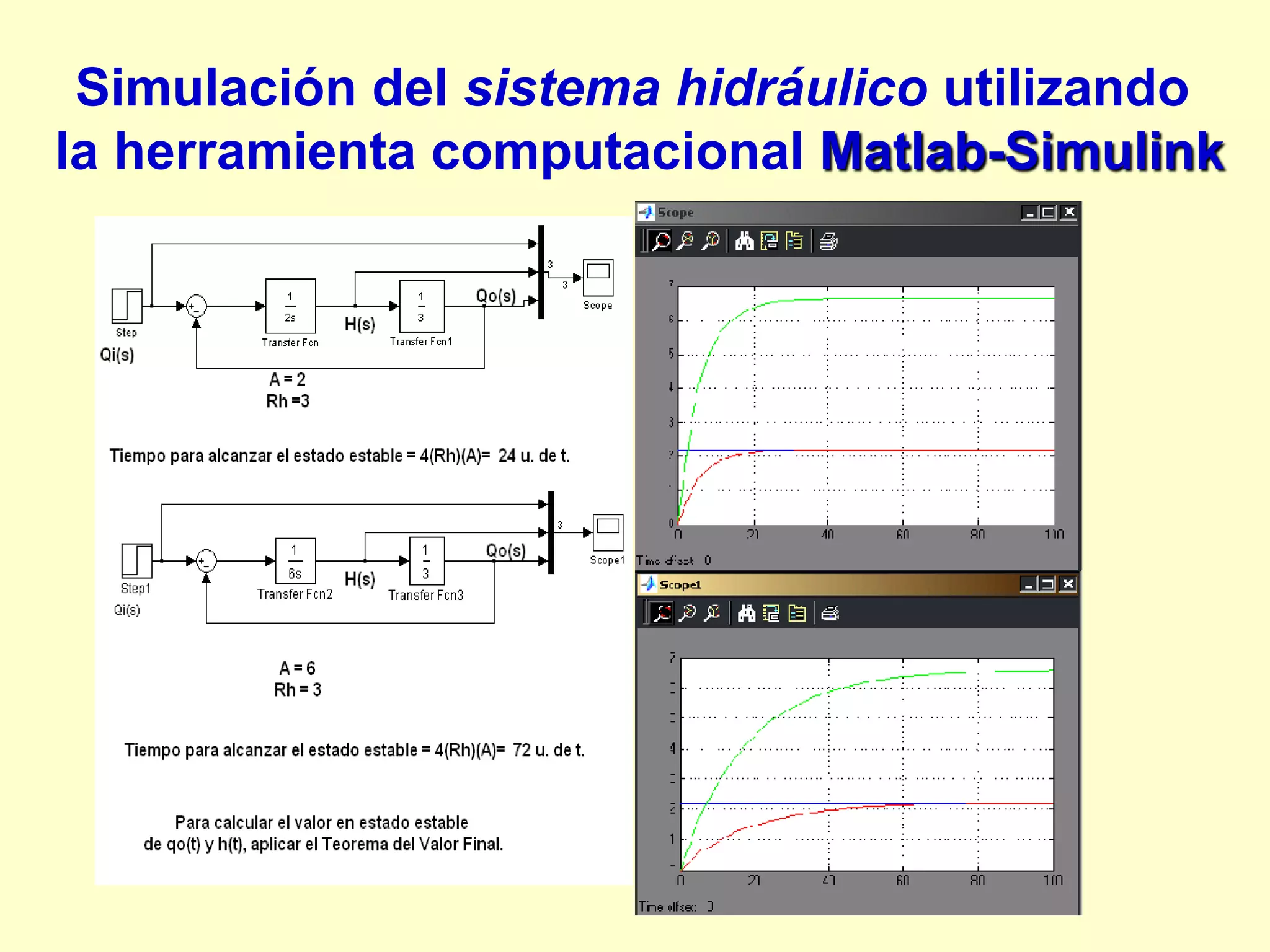
0
.,
.
2
)
(
;
.
.
8
.
0
)
0
(
);
(
2
.
1
)
(
)
(
10





t
para
i
de
u
t
u
i
de
u
y
t
u
t
y
dt
t
dy
cia
Transferen
de
Función
s
s
s
G
s
U
s
Y
s
U
y
s
s
Y
s
U
s
Y
y
s
sY
t
u
t
y
dt
t
dy
i
c
:
1
.
0
12
.
0
1
10
2
.
1
)
(
)
(
)
(
);
(
)
0
(
10
]
1
10
)[
(
);
(
)
(
)
0
(
10
)
(
10
)}
(
{
)}
(
)
(
10
{
| 0
.
.














L
L
jw

X
-0.1
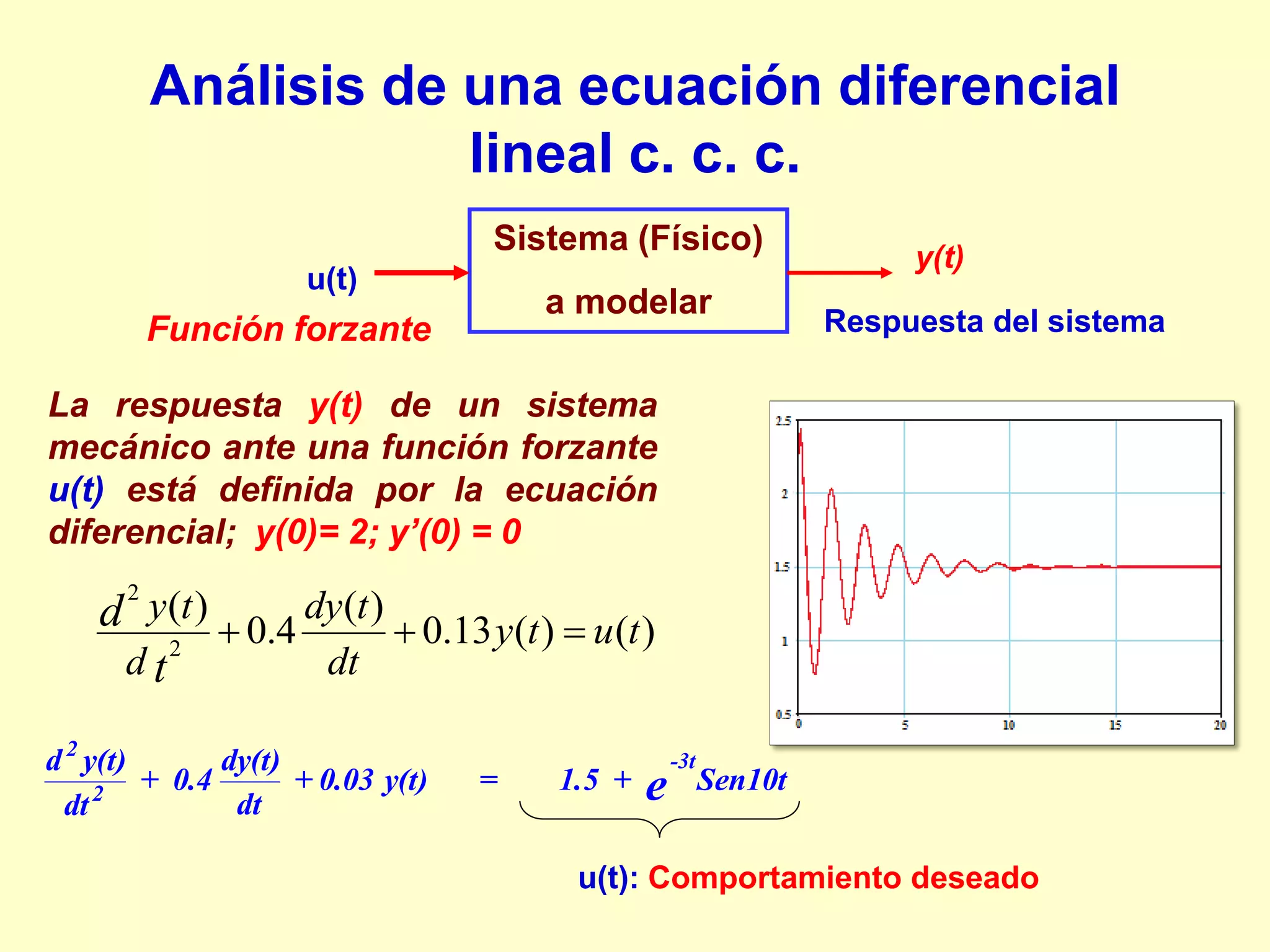
Para la ecuación diferencial
Solución:
Respuesta
Función
:
)
1
.
0
(
)
3
.
0
(
8
.
0
)
1
10
(
4
.
2
8
)
(
4
.
2
8
8
2
2
.
1
]
1
10
)[
(
;
2
2
.
1
)
8
.
0
(
10
]
1
10
)[
(
);
(
2
.
1
)
(
)
0
(
10
)
(
10
)}
(
2
.
1
{
)}
(
)
(
10
{































s
s
s
s
s
s
s
Y
s
s
s
s
s
Y
s
s
s
Y
s
U
s
Y
y
s
sY
t
u
t
y
dt
t
dy
L
L
jw

o X X
-0.3 -0.1 0
Obtener: a) G(s) y, b) Y(s)

14. Obtención del valor inicial y final de y(t)
Respuesta
Función
:
)
1
.
0
(
)
3
.
0
(
8
.
0
)
1
10
(
4
.
2
8
)
(






s
s
s
s
s
s
s
Y
1
.
0
6
.
1
4
.
2
1
.
0
)
(






s
s
s
b
s
a
s
Y
0.8
















 1
8
.
0
)
1
.
0
(
)
3
.
0
(
8
.
0
)
1
.
0
(
)
3
.
0
(
8
.
0
.
)
(
.
)
0
(
:
lim
lim
lim
lim
s
s
s
s s
s
s
s
s
s
s
Y
s
y
inicial
valor
del
Teorema
jw

o X X
-0.3 -0.1 0
4
.
1
.
0
)
3
.
0
)(
8
.
0
(
)
1
.
0
(
)
3
.
0
(
8
.
0
)
1
.
0
(
)
3
.
0
(
8
.
0
.
)
(
.
)
(
:
final
valor
del
Teorema
lim
lim
lim
0
0
0
2












 s
s
s
s
s
s
s
Y
s
y
s
s
s
2.4
0.8
t
Polo dominante

15. Gráfica aproximada de y(t) a partir de Y(s)
1
200
1600
)
(
1600
]
1
200
)[
(
;
0
)
(
)
0
(
200
)
(
200
80
)
0
(
;
0
)
(
)
(
200











s
s
Y
s
s
Y
s
Y
y
s
sY
C
y
t
y
dt
t
dy
80
200
1600
1
200
1600
)
(
)
0
( lim
lim 







 s
s
s
sY
y
s
s
0
1
200
1600
)
(
)
( lim
lim
0
0






 s
s
s
sY
y
s
s
Un horno que se encuentra a 80°C se apaga para su enfriamiento.
Considere que la relación Temperatura-flujo combustible, es representada
por la ecuación Diferencial: 200y´(t) + y(t) = K u(t). Obtenga, y(0) y y()
Teorema de valor inicial:
Teorema del valor final:
t
80 ºC
0 ºC

16. Programa MATLAB-SIMULINK (basado en
la representación a bloques)
• Para modelar y analizar los elementos de una
ecuación diferencial a partir de las ecuaciones de un
sistema físico.
• Obtener la respuesta en el tiempo para una función
Y(s).
• Obtener las gráficas de las diferentes variables
dentro de mismo sistema físico, sin requerir obtener
su representación en el tiempo.
• …

17. Modelación de una ecuación diferencial
mediante Diagrama a bloques.
1
As
o 0
i
H(s)
(s) H(s) (
s , 0)
s s)
( ;
) Q
Q Q
A (c. i.
Rh
   
1
Rh
Caudal de
salida
Caudal
Acumulado
=
Qi(s) +
Qo(s)
H(s) Qo(s)
Qi(s) – Qo(s)
qo(t): Caudal de salida
qi(t): Caudal de entrada
A:
área del tanque
p(t): señal que regula
el caudal hacia el tanque.
h(t): altura del tanque
Rh: resistencia Hidráulica
Caudal de
entrada
)
1
(
......
dt
dh(t)
A
Av(t)
(t)
(t)
(t) q
q
q acum
0
i




(2)
.....
Rh
h(t)
(t)
q0


18. Simulación del sistema hidráulico utilizando
la herramienta computacional Matlab-Simulink

19. Dos Tanques
dt
t
dh
A
t
t
t
t q
q
q
q acum
i
)
(
)
(
)
(
)
(
)
( 02
01




R
q
R
q
h
h
t
h
t
t
h
t
2
02
1
01
)
(
)
(
;
)
(
)
(


As
1
)
(
)
(
)
(
)
(
)
( 02
01
s
H
s
A
s
s
s
s Q
Q
Q
Q acum
i




R
Q
R
Q
h
h
s
H
s
s
H
s
2
02
1
01
)
(
)
(
;
)
(
)
(


Rh1
1
Rh2
1
H(s)
Qi(s)
Qi(s) – Q01(s) – Q02(s)
Q01(s)
Q02(s)
-
+
-
h(t)
qi(t)
Rh1
Rh2
q01(t)
A
p(t)
q02(t)
V1 V2

20. Modelaciòn y simulación del sistema de
dos tanques mediante SIMULINK.

21. Gráficas de Simulación
(tanque_1entrada_2salidas)
Flujo de salida q02(t)
Flujo de salida q02(t)
h(t): Altura (nivel de llenado) del tanque
Qi(t): Flujo de entrada

22. Sistema: Masa-Resorte-Amortiguador
en la suspensión de un auto
Masa: m
Amortiguador
Resorte
z(t): desplazamiento
o respuesta del sistema
f(t)entrada: fuerza de entrada
t
d
d
t
z
m
ma
fuerzas
i
2
2
1
)
(





23. Aplicación del sistema básico:
masa-resorte-amortiguador

24. Simulación mediante SIMULINK
 

t
d
d
t
z
m
ma
Fuerzas 2
2
)
(
dt
dz(t)
B
)
(
)
(
)
(
)
(
)
(
)
(






t
f
t
f
t
f
t
f
f
or
amortiguad
resorte
or
amortiguad
resorte
i
t
z
k
t
fuerzas
Z(s)
k
B s
s
m 2
1
Fi(s)
F(s)resorte
F(s)amortiguador
Fi(s) - F(s)resorte – F(s)amortiguador = m s2 Z(s)
-
+
-
)
(
)
(
)
(
)
(
s
sZ
B
s
Z
k
s
F
s
F
or
amortiguad
resorte


fi(t)
z(t)

25. Masa-Resorte-Amortiguador con SIMULINK

26. Paso por un bache sencillo

27. Masa-Resorte-Amortiguador en terrenos
con superficie rugosa.