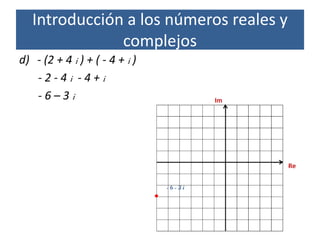
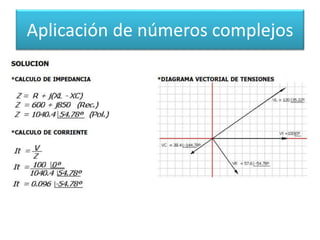
El documento es un syllabus del curso de álgebra en la Universidad Veracruzana, abarcando temas como números reales y complejos, ecuaciones lineales, matrices y transformaciones lineales. Se establece un cronograma académico y criterios de evaluación, donde los estudiantes deben aprobar con una calificación mínima de 6 en los exámenes parciales y ordinarios. Incluye fundamentos sobre números complejos, su representación, operaciones y conceptos relacionados como el módulo y argumento.

1. Álgebra
Universidad Veracruzana
Facultad de Ingeniería
Mtro. Javier Andrés Tiburcio García
Agosto/16-Enero/17

2. Temas
1. Números reales y
complejos
2. Ecuaciones de grado
superior
3. Matrices y
determinantes
4. Ecuaciones lineales
5. Estructuras algebraicas
6. Espacios vectoriales
7. Espacios con producto
interno
8. Transformaciones
lineales
9. Valores propios,
vectores propios y
formas cuadráticas

3. Cronograma académico de Algebra

4. Criterios de evaluación
• Promedio de 3 exámenes parciales y examen
ordinario.
• Calificación mínima para aprobar: 6.

5. Fuentes de información

6. 1. NÚMEROS REALES Y COMPLEJOS
Álgebra

7. Introducción a los números reales y
complejos
i = Unidad imaginaria
Aquel número que al elevarlo al cuadrado nos da como resultado -1.
i 2= -1
Definición:
Raíz cuadrada principal de -1.
i = −𝟏

8. Introducción a los números reales y
complejos
Potencias de i
i 0=
i 1=
i 2=
i 3=
i 4=
i 5=
i 6=
i 7=

9. Introducción a los números reales y
complejos
Potencias de i
i 0= 1
i 1= i
i 2= -1
i 3= i 2 *i1=(-1)* i= -i
i 4= i 3 *i1= (- i)*i= -i 2=-(-1)=1
i 5= i 4* i1=(1)*(i)=i
i 6= i 4* i2=(1)*(-1)=-1
i 7= i 4 *i3=(1)* -i= -i

10. Introducción a los números reales y
complejos
Potencias de i
i n= i 4c+r=i 4c*ir=(i 4)c*ir=(1)*ir=ir
11034
275
30
23
3
Ejemplo:
i 1103=(i 4)275i 3=(1)*i 3=-i
c
r

11. Introducción a los números reales y
complejos
Ejemplo:
i 2026=
Ejemplo:
i 7320=

12. Introducción a los números reales y
complejos
20264
506
026
2
Ejemplo:
i 2026=(i 4)506i 2=(1)*i 2=-1
c
r
73204
1830
33
12
0
Ejemplo:
i 7320=(i 4)1830i 2=(1)*i 0=1
c
r

13. Introducción a los números reales y
complejos
Ejemplo:
Raíces imaginarias de números negativos
−𝑥 = (−1)(𝑥) = i 𝑥
−36 = (−1)(36) = i 36 =6i
Ejemplo:
−11 = (−1)(11) = 11i

14. Introducción a los números reales y
complejos
Ejemplos:
−48 =
−12 48 =
−52 =
−32 =

15. Introducción a los números reales y
complejos
Ejemplo:
−48 = (−1)(48)
48 2
24 2
12 2
6 2
3 3
−48 = −1 2 2 2 (2)(3)
−48 = −1 (16)(3)
−48 = −1 (16) (3)
−48 = 4 (3) i

16. Introducción a los números reales y
complejos
Ejemplo:
−52 = (−1)(52)
52 2
26 2
13 13
−52 = −1 2 2 13
−52 = −1 (4)(13)
−52 = 2 (13) i

17. Introducción a los números reales y
complejos
Ejemplo:
−32 = (−1)(32)
32 2
16 2
8 2
4 2
2 2
−32 = −1 2 2 2 (2)(2)
−32 = −1 (16)(2)
−48 = −1 (16) (2)
−48 = 4 (2) i

18. Introducción a los números reales y
complejos
Ejemplo:
−12 48 = (−1)(12)(48)
48 2
24 2
12 2
6 2
3 3
−12 48 = −1 12 48
−12 48 = (2)(4) −1 (3) 3
−12 48 = 8 −1 (3)(3)
−12 48 = 24 i
−12 48 = −1 4)(3 2)(2)(2)(2)(3

19. • Un número complejo puede ser representado por
una expresión de la forma
a + bi
• a y b son números reales
• i es un símbolo con la propiedad de que
i2 = -1
• Ejemplos:
2 + 3i -2 – 2i
3 – 2i -4 + 2i
Introducción a los números reales y
complejos

20. • El número complejo a + bi también puede ser
representado por el par ordenado (a,b) y trazado en
un plano (llamado Plano Argand) .
• 2 + 3i
• -2 – 2i
• 3 – 2i
• -4 + 2i
Introducción a los números reales y
complejos
Números complejos como
puntos en el plano Argand.

21. • La parte real del número complejo a + bi es el
número real a y la parte imaginaria es el número real
b.
2 + 3 i
• Dos números complejos a + bi y c + di son iguales si
a=c y b=d
• Esto es, sus partes reales son iguales y sus partes
imaginarias son iguales.
Introducción a los números reales y
complejos
Parte real: 2
Parte imaginaria: 3

22. • La suma y diferencia de dos números complejos
están definidas al sumar o restar sus partes reales y
sus partes imaginarias:
(a+bi) + (c+di) = (a+c) + (b+d)i
(a+bi) - (c+di) = (a+c) - (b+d)i
• Por ejemplo:
(1 - i) + (4 + 7i) = (1 + 4) + (-1 + 7)i = 5 + 6i
Introducción a los números reales y
complejos

23. • El producto de números complejos se define de
modo que se cumplan las leyes conmutativa y
distributiva:
(a+bi) (c+di) = a(c+di) + (bi)(c+di)
= ac + adi + bci + bdi 2
• Como i2 = -1, esto se convierte en
(a+bi) (c+di) = (ac – bd) + (ad + bc)i
• Por ejemplo:
(-1 +3i ) (2 - 5i ) = (-1)(2 - 5i ) + 3i (2 - 5i )
= -2 + 5i + 6i – 15(-1)= 13 + 11 i
Introducción a los números reales y
complejos

24. Introducción a los números reales y
complejos
Ejemplos de producto de números complejos

25. Ejemplo:
Simplifica y traza en el plano Argand las siguientes
expresiones:
a) 2 + 3i + 7i 2 + 5i 3 + 9i 4
b) 5i 22 + 2
c) 2 (– 1 – 4 i ) + ( 3 + 2i )
d) - (2 + 4 i ) + ( - 4 + i )
e) -(4 - 2i ) + (- 5 – i )
Introducción a los números reales y
complejos

26. a) 2 + 3i + 7i 2 + 5i 3 + 9i 4
2 + 3i + 7 (-1) + 5 (-i ) + 9 (1)
4 - 2i
Introducción a los números reales y
complejos

27. b) 5i 22 + 2
5 (i 4 )5 (i 2) + 2
5 (1) (-1) + 2
-5 + 2
-3 + 0i
Introducción a los números reales y
complejos

28. c) 2 (– 1 – 4 i ) + ( 3 + 2i )
- 2 – 8 i + 3 + 2i
1 – 6 i
Introducción a los números reales y
complejos

29. d) - (2 + 4 i ) + ( - 4 + i )
- 2 - 4 i - 4 + i
- 6 – 3 i
Introducción a los números reales y
complejos

30. e) -(4 - 2i ) + (- 5 – i )
-4 + 2i - 5 – i
-9 + i
Introducción a los números reales y
complejos

31. Conjugado de un número complejo:
Se llama conjugado de un número complejo al número
complejo que se obtiene por simetría del dado
respecto del eje de abscisas.
Introducción a los números reales y
complejos
a + b i = a – b i
z = a + b i
z = a - b i

32. Introducción a los números reales y
complejos
El producto de un número complejo por su conjugado es un número real.

33. • La división de números complejos es muy semejante
a racionalizar el denominador de una expresión
racional.
• Para el número complejo :
z= a+bi
• Se define su complejo conjugado como
=a - bi
• Para hallar el cociente de dos números complejos
multiplique el numerador y el denominador por el
conjugado complejo del denominador.
Introducción a los números reales y
complejos
z

34. • Ejemplo:
Exprese el número
−1+3𝑖
2+5𝑖
en la forma a + bi
Multiplique el numerador y el denominador por
el conjugado complejo de 2 + 5i, es decir 2 – 5i.
−1 + 3𝑖
2 + 5𝑖
=
−1 + 3𝑖
2 + 5𝑖
∙
2 − 5𝑖
2 − 5𝑖
=
13 + 11𝑖
22 + 52
=
13
29
+
11
29
𝑖
Introducción a los números reales y
complejos

35. • Ejemplo:
Introducción a los números reales y
complejos

36. • Ejemplo:
Introducción a los números reales y
complejos

37. • Ejemplo:
Introducción a los números reales y
complejos

38. • Ejemplo:
Introducción a los números reales y
complejos

39. • Ejemplo:
Introducción a los números reales y
complejos

40. • Ejemplo:
Introducción a los números reales y
complejos

41. Introducción a los números reales y
complejos

42. Razones trigonométricas de ángulos
notables

43. Módulo de un número complejo
El módulo de un número complejo es el módulo
del vector determinado por el origen de
coordenadas y su afijo. Se designa |z|.
r2=a2 + b2

44. Módulo de un número complejo
Ejemplos:

45. Argumento de un número complejo
• Se llama argumento de un número complejo
al ángulo que forma el semieje real con el
segmento que une el origen de coordenadas y
el afijo del número.
• Se representa por arg(z) o simplemente por α.

46. Argumento de un número complejo

47. Argumento de un número complejo

48. Argumento de un número complejo

49. Forma polar de un número complejo

50. Forma polar de un número complejo

51. Forma polar de un número complejo

52. Forma polar de un número complejo

53. Forma polar de un número complejo

54. Forma polar de un número complejo

55. Aplicación de números complejos
Ω

56. Aplicación de números complejos

57. Aplicación de números complejos

58. Aplicación de números complejos

59. Aplicación de números complejos