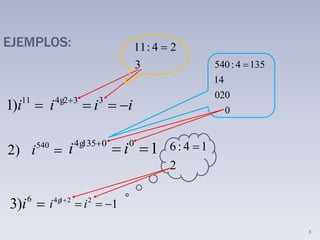
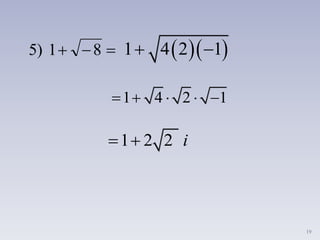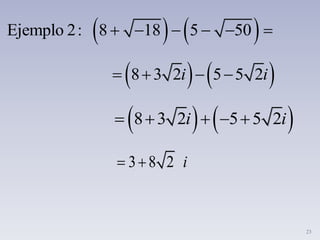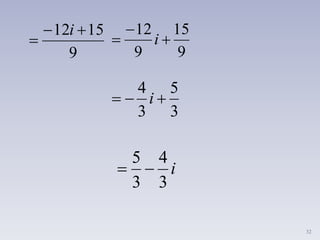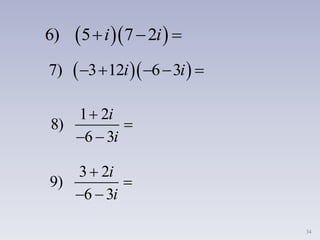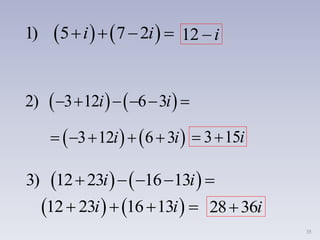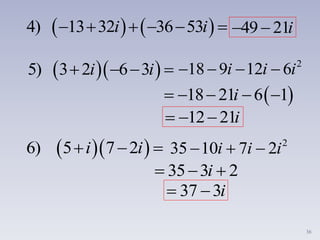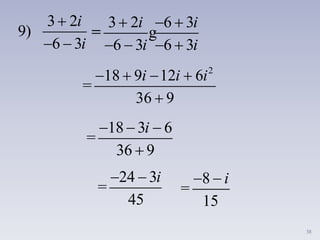i. Los números imaginarios surgen de la necesidad de resolver ecuaciones cuadráticas sin solución en los números reales. Un número imaginario es un número cuya raíz cuadrada es negativa y puede escribirse como ib, donde b es un número real y i es la unidad imaginaria tal que i2 = -1. ii. Los números complejos amplían el conjunto de los números reales para incluir tanto los números reales como los imaginarios y permiten resolver ecuaciones antes insolubles. Un número complejo puede escribirse como z = a + bi, donde a es la parte real y b la

1. 1

2. Un número imaginario es un número cuyo
cuadrado es negativo.
Este término fue destacado por René Descartes
en el siglo XVII y expresaba claramente sus
creencias: obviamente tales números no
existen. Hoy en día ubicamos los números
imaginarios sobre el eje vertical del plano
complejo. Cada número imaginario puede ser
escrito como
ib (numero complejo)
donde b es un verdaderonúmero real e i es la
unidad imaginaria con la propiedad:
i2 = − 1 2

3. 3
DEFINICIÓN: Los Números Imaginarios surgen de
la necesidad de resolver ecuaciones cuadráticas
sin solución en el campo real.
Este conjunto se representa por i
 Este conjunto posee elementos que se obtienen
a partir de raíces cuadradas con cantidad
subradical negativa.
7
3 2
3 10 

4. 4
Definición:
Entenderemos como Unidad Imaginaria a:
La que se conoce como Raíz Imaginaria.
i= -1
Nota: 2
i =-1

5. NÚMEROS IMAGINARIOS
 Luego:
 
16
16 1
16 1
4i
 
  
  


6.  Se definió un número cuyo cuadrado es -1
 después del año 1777, Euler lo denominó con la
letra “i”.
2
i =-1

7. 7
POTENCIAS DE I:
1. Divida el exponente por 4 y el resultado será elevado al resto de
la división.
2. luego para simplificar use;
3. Sí
2
i =-1
 3 2
i =i i=-1 i=-i
  4 2 2
i =i i = -1 -1 =1
Este último resultado hace que las potencias de “i” solo
tengan como resultados a: i, -i, 1 y -1
0
i =1
1
i =i
n 4m+p p
i =i =i
i= -1

8. 8
EJEMPLOS:
4 1 2 2
1i i
  g
6: 4 1
2

4 2 3 3
i i i
  g11
1)i 
540
2) i 
4 135 0 0
1i i
 g
11: 4 2
3

540: 4 135
14
020
0

6
3)i 

9. 9
3
i 
13
4) i  i
227
5) i  i
285
6) i 
1
i
1127
7) i  i
285 4 71 1 g
i
1127 4 281 3 g
3
i 

10. 10
Calcule las siguientes raíces:
4 1  
11 i
25 1  
1) 4 
2) 25 
3) 12 
4) 11 
i2
i5
2 3 i4 3 1  
Raíces pares de Números Negativos

11. NÚMEROS COMPLEJOS
 Hallar los números reales que verifican que
la suma entre el quíntuplo de su cuadrado y
20, es igual a cero.
 En símbolos:
2
5 20 0x  

12. 12

13. NÚMEROS COMPLEJOS
 Al resolver la ecuación obtenida, nos damos
cuenta que la raíz cuadrada de un número
negativo no existe en los reales, por lo
tanto esta ecuación no tiene solución en este
conjunto, es decir que no existe ningún
número real que resuelva este problema.
(Sin solución real)
2
5 20 0x  

14. NÚMEROS COMPLEJOS
 Para que la ecuación anterior tenga solución,
los matemáticos buscaron una ampliación
del conjunto de los Números Reales (IR).
 A este Conjunto se definió como los
Números Complejos:
 / , ;a bi a bi   £ ¡ I

15. © copywriter
15
i) Los números reales y los
imaginarios están incluidos en
el conjunto ampliado.
ii) Las propiedades del
conjunto real se siguen
cumpliendo en el conjunto
ampliado.
Sus características son:

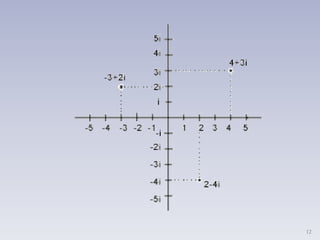
16. NÚMEROS COMPLEJOS
 Se llama número complejo a un número “z”
que puede escribirse de la forma
 a y b son números reales
 Al número a se le llama parte real (a=Re[z])
 Al número b se le llama parte imaginaria
(b=Im[z])
z=a+bi
a+bi (a,b)

17. IGUALDAD DE NÚMEROS COMPLEJOS:
 Dos Números complejos son iguales si y
sólo si, tienen igual parte real e igual parte
imaginaria
 si
 Entonces:
1 2z =z
       1 2 1 2Re z =Re z Im z =Im z
Ó sí a + bi = c + di entonces a = c y b = d.

18. 18
Ejemplos de Números Complejos:
i35)1 
i47)2 
i61)3 
i5)4
7)5

19. 19
 81)5   1 4 2 1 
1 2 2 i 
1 4 2 1    

20. 20
Ejemplo:
Determine el valor de y de si
  ibia 5626 
66Si a 2 5y b  
0a
2
5
b
a b

21. 21
OPERACIONES CON NÚMEROS COMPLEJOS
   a bi c di  1.Suma:
   idbca 
   Ej 5em 1: 6plo 2   i i
   5 6 1 2    i
i11

22. 22
   a bi c di  2.Resta:
   idbca 
   3Ejemplo 1: 2 6 3    i i
   3 2 6 3i i   
9 5i 
   a bi c di    
Obs:La resta se cambia a la suma del opuesto del sustraendo.

23. 23
   Ejemplo 2: 8 18 5 50     
   8 3 2 5 5 2i i   
   8 3 2 5 5 2i i    
3 8 2 i 

24. 24
   a bi c di g3.Multiplicación:
   ac bd ad bc i   
Nota: La multiplicación se puede llevar a cabo como si
fuera una multiplicación de polinomios.
  a bi c di   ac ad i  bc i  2
bd i 
   1ac ad bc i bd    
   ac bd ad bc i   

25. 25
  Ejemplo 1: 4 2 3 5  i i
2
1062012 iii 
12 14 10i  
i1422
 12 20 6 10 1i i    

26. 26
 
2
Ejemplo 2: 4 5 i
254016  i
i409
  4 5 4 5i i  
2
16 20 20 25i i i   
 16 40 25 1i   

27. 27
 
3
Ejemplo 3: 2 3 i
46 9i  
   
2
2 3 2 3i i 
  2
4 12 9 2 3i i i   
   4 12 9 1 2 3i i    
  4 12 9 2 3i i   
  5 12 2 3i i   
2
10 15 24 36i i i    
10 15 24 36i i    

28. 28
.El conjugado de
Conjugado de un C
z=a+bi sedefin
ompl
e po
ejo:
Definició
r Z=a+bi=a
n
-bi
:
Encuentra el conjugado de cada
Ejemplo
núm
s:
ero:
1. 2 4
2. 2 4
3. 64
4. 12 24
5. 13
i
i
i
i
 
 

 

i42
2 4i
64i
12 24i
13

29. 29
8 7
:
1 3
i
i



Ejemplo 1
(8 7 )
•
(1 3 )
(1 3 )
(1 3 )
ii
i i


2
2
91
217248
i
iii



La División se hace multiplicando por el conjugado
del denominador. (similar a la racionalización)
 
 
a bi
c di



4.División: .
a bi c di
c di c di
   
   
 

  

30. 30
 
 
8 17 21 1
1 9 1
i  

 
8 17 21
1 9
i 

 10
1729 i

i
10
17
10
29


31. 31
4 5
:
3
i
i

Ejemplo 2 (4 5 )
•
3
3
3i i
i i 

2
2
9
1512
i
ii



9
1512 

i

32. 32
9
1512 

i
9
15
9
12


 i
3
5
3
4
 i
i
3
4
3
5


33. 33
Ejercicios:
Resuelve la operación indicada.
   1) 5 7 2i i   
   2) 3 12 6 3i i     
   3) 12 23 16 13i i    
   4) 13 32 36 53i i     
  5) 3 2 6 3i i   

34. 34
  6) 5 7 2i i  
  7) 3 12 6 3i i    
1 2
8)
6 3


 
i
i
3 2
9)
6 3


 
i
i

35. 35
   1) 5 7 2i i    12 i
   2) 3 12 6 3i i     
   3 12 6 3    i i 3 15  i
   3) 12 23 16 13i i    
   12 23 16 13   i i 28 36 i

36. 36
   4) 13 32 36 53i i      49 21  i
  5) 3 2 6 3i i    2
18 9 12 6   i i i
 18 21 6 1    i
12 21   i
  6) 5 7 2i i   2
35 10 7 2  i i i
35 3 2  i
37 3  i

37. 37
  7) 3 12 6 3i i     2
18 9 72 36   i i i
18 63 36  i
54 63  i
1 2
8)
6 3


 
i
i
1 2 6 3
6 3 6 3
  

   
i i
i i
2
2
6 3 12 6
36 9
   


i i i
i
6 9 6
36 9
  


i 12 9
45
 
 
i 4 3
15
  i

38. 38
3 2
9)
6 3


 
i
i
3 2 6 3
=
6 3 6 3
  
   
g
i i
i i
2
18 9 12 6
=
36 9
   

i i i
18 3 6
=
36 9
  

i
24 3
=
45
  i 8
=
15
  i

39. REPRESENTACIÓN GRÁFICA:
 Para representar un número complejo, de la
forma se utiliza un sistema de
coordenadas rectangulares, en el cual la
parte real se representa en el eje horizontal y
la imaginaria en el eje vertical.
 Obs:
a+bi
a+bi (a,b)

40. Ejemplos:

42. Módulo de un Complejo:
 Es la distancia entre el origen y el punto
que representa al número complejo.
 El módulo de un número complejo
está definido como:
 Ejemplo:
2 2
a+bi = a +b
2 2
(-4) +2 = 20 =2 5-4+2i
a+bi