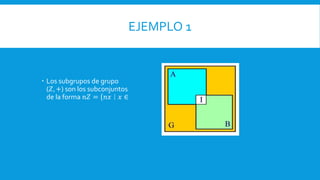
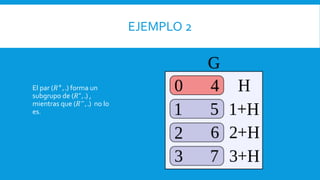
Este documento define conceptos matemáticos como grupo, subgrupo, anillo y cuerpo. Un grupo es un conjunto con una operación binaria que cumple propiedades como asociatividad, elemento neutro e inverso. Se presentan ejemplos de grupos como números enteros con suma. Un subgrupo es un subconjunto de un grupo que también forma un grupo. Un anillo es un conjunto con dos operaciones, una de las cuales hace de él un grupo conmutativo. Un cuerpo es un anillo conmutativo donde todo elemento distinto de cero tiene inverso.

1. MATEMÁTICAS DISCRETAS
Junior Peña 16-0846
EnmanuelVeras 17-0316

2. GRUPO

3. DEFINICION
En álgebra abstracta, un grupo es un conjunto en el
que se define una operación binaria, que satisface
ciertos axiomas. La rama de la matemática que
estudia los grupos se llama teoría de grupos.
Sea una estructura algebraica formada por un
conjunto G, sobre cuyos elementos se ha definido
una operación o ley de composición interna binaria
denotada por "O". Se dice que la estructura (G;O) es
un grupo con respecto a la operación si satisface las
siguientes propiedades:

4. PROPIEDADES DE UN GRUPO
• Asociatividad: para cualesquiera elementos del grupo no importa el orden en que se operen las
parejas de elementos, mientras no se cambie el orden de los elementos (ver grupo abeliano),
siempre dará el mismo resultado.
• Existencia del elemento neutro o elemento identidad (comúnmente denotado como e, letra
inicial de la palabra alemana einheit, que significa "unidad"): en todo grupo existe un elemento
que al ser operado con cualquier otro, no lo modifica, (como el cero en la suma o el 1 en la
multiplicación).
• Existencia de elemento opuesto (o inverso):Todos los elementos del grupo tienen un elemento
opuesto (o inverso), con el que al operarse dan por resultado el elemento neutro e.
Algunos textos incluyen para los grupos la propiedad de la cerradura, pero generalmente se la
obvia al ser propiedad de la operación binaria. Esta ley se la formula de la siguiente manera:
• Cerradura: para cualesquiera dos elementos del grupo G operados bajo " ", el resultado siempre
pertenece al mismo grupo G. Es decir, para toda x, y E G, x o y E G
La propiedad de la cerradura del grupo se expresa generalmente como GxG->G

5. TIPOS DE GRUPOS
 Grupo abeliano (o conmutativo). Se denomina grupo conmutativo o abeliano a
aquel grupo que verifica la Propiedad conmutativa, es decir a.b=b.a para toda a, b
E G.
 Grupo abeliano de torsión. Un grupo abeliano A se dice de torsión si todo
elemento de A es de torsión.
 Grupo finito. Es un grupo con un número finito de elementos.
 Grupo de Lie. Es un grupo que además tiene estructura de variedad diferenciable.
 Grupo cíclico. Es un grupo conmutativo, finito o infinito, que puede ser generado
por multiplicación reiterada de un sólo elemento.

6. EJEMPLO 1
En un grupo conmutativo:
 La suma define estructura de grupo conmutativo en el conjunto
de los números enteros (Z), en los numeros racionales (Q), en
los numeros reales (R) y en los umeros complejos (C).
 Los vectores libres del espacio, con la suma de vectores,
forman un grupo conmutativo.
 La suma de matrices define una estructura de grupo
conmutativo en las matrices con coeficientes reales con un
número de columnas y filas prefijado.
 Las funciones reales de variable real, con la suma de funciones,
también forman un grupo conmutativo, al igual que las
sucesiones de números reales con la suma de sucesiones.

7. EJEMPLO 2
 Los siguientes ejemplos lo son del concepto de Grupo de Lie, que son los grupos
definidos por operaciones continuas sobre curvas superficies o variedades de
dimensión mayor:
 El grupo de los movimientos del espacio o grupo de isometría del espacio
euclídeo, el grupo de las semejanzas del plano o el grupo de las afinidades de una
recta (las aplicaciones de la forma x-->ax+b con a distinto de cero).
 El grupo de Galileo, formado por las transformaciones del espacio y el tiempo que
conservan los sistemas de referencia inerciales.
 El grupo de Lorentz de la teoría de la relatividad, etc.

8. SUBGRUPO

9. DEFINICION
 Dado un grupo G con una operación binaria *, se dice que un subconjunto no vacío
H de G es un subgrupo de G si H también forma un grupo bajo la operación *. O de
otro modo, H es un subgrupo de G si la restricción de * a H satisface los axiomas
de grupo.
 Un subgrupo propio de un grupo G es un subgrupo H que es un subconjunto
propio de G (es decir H ≠ G). El subgrupo trivial de cualquier grupo es el subgrupo
{e} que consiste solamente en el elemento identidad.
 El grupo G a veces se denota por el par ordenado (G, *), generalmente para
acentuar la operación * cuando G lleva varias estructuras algebraicas o de otro
tipo. En lo siguiente, se sigue la convención usual y se escribe el producto a*b
como simplemente ab.

10. PROPIEDADES DE UN SUBGRUPO
 Todo grupo G con más de un elemento tiene al menos dos subgrupos:
 el subgrupo trivial {e}, que contiene sólo al elemento identidad.
 el mismo G, que es el subgrupo máximo de G.
 Dados dos subgrupos H y K de un grupo G, la intersección H ∩ 𝐾es un subgrupo.
En general, la unión de subgrupos no forma un subgrupo, salvo que uno de ellos
esté contenido en el otro.
 Todo elemento a de un grupo G genera un subgrupo cíclico <a>.
 Si S es un subconjunto de G, entonces existe un subgrupo mínimo de G que
contiene S: es el subgrupo generado por S y se denota por <S>. Un elemento de G
está en <S> si y solamente si es un producto finito de elementos de S y de sus
inversos.

11. EJEMPLO 1
 Los subgrupos de grupo
(𝑍, +) son los subconjuntos
de la forma 𝑛𝑍 = 𝑛𝑥 ⋮ 𝑥 ∈

12. EJEMPLO 2
El par (𝑅+
, .) forma un
subgrupo de (𝑅∗
, .) ,
mientras que (𝑅−, .) no lo
es.

13. ANILLO

14. ANILLO: DEFINICIÓN
 Un anillo es un sistema algebraico formado por un
conjunto no vacío y dos operaciones internas, llamadas
usualmente suma y producto, que cumplen ciertas
propiedades.
 Sea (A, ∗1, ∗2) un conjunto A con dos operaciones ∗1 y ∗2.
Se llamaAnillo si se verifican estas tres condiciones:
 (A, ∗1) es un grupo conmutativo
 (A, ∗2) tiene las propiedades asociativa y la de tener un
elemento neutro.
La propiedad distributiva de la segunda operación
respecto de la primera, es decir si para todo a, b, c ∈ A se
cumple que: a ∗2 (b ∗1 c) = (a ∗2 b) ∗1 (a ∗2 c).

15. ANILLO: EJEMPLO 1
 El ejemplo típico de anillo (conmutativo) es (Z+, ×) el
conjunto de los enteros con la suma y el producto. Notemos
lo siguiente:
Para la primera operación (suma):
El conjunto de los números enteros es cerrado para la suma.
La operación suma es asociativa.
La operación suma tiene un elemento neutro.
La operación suma tiene un elemento simétrico para los
números enteros.
Para la segunda operación (multiplicación):
El conjunto de los números enteros es cerrado para la
multiplicación.
La operación multiplicación es asociativa.
La operación multiplicación es distributiva respecto a la
suma.

16. ANILLO: EJEMPLO 2
 Sea Mn el conjunto de las matrices cuadradas de orden n, puede
decirse que Matriz cuadrada es un anillo:
Para todas las matrices cuadradas de n filas A y B, A+B también es
una matriz cuadrada de n filas y columnas.
La suma de matrices cuadradas del mismo orden n es asociativa.
La suma de matrices cuadradas del mismo orden n es conmutativa.
Z es el neutro para la suma.
Para toda matriz cuadrada de n filas y columnas Matriz n se tiene su
inverso dado por Matriz n cuadrada y según la suma de matrices
Cancelacion matrices n.
El producto de matrices cuadradas de orden n es cerrado.
El producto de matrices cuadradas de orden n es asociativo.
Para todas matrices cuadradas de orden n A, B, C se cumple
A(B+C)=AB+AC.

17. CUERPO

18. CUERPO: DEFINICIÓN
 Un cuerpo es un anillo de división conmutativo, es decir,
un anillo conmutativo y unitario en el que todo
elemento distinto de cero es invertible respecto del
producto. Por tanto un cuerpo es un conjunto K en el
que se han definido dos operaciones, + y ·, llamadas
adición y multiplicación respectivamente, que cumplen
las siguientes propiedades:
K es cerrado para la adición y la multiplicación
 Para todo a, b en K, a + b y a · b pertenecen a K (o más
formalmente, + y · son operaciones matemáticas en K);
Asociatividad de la adición y la multiplicación
 Para toda a, b, c en K, a + (b + c) = (a + b) + c y a · (b · c) =
(a · b) · c.

19. CUERPO: DEFINICIÓN (CONT.)
Conmutatividad de la adición y la multiplicación
 Para toda a, b en K, a + b = b + a y a · b = b · a.
Existencia de un elemento neutro para la adición y la multiplicación
 Existe un elemento 0 en K, tal que para todo a en K, a + 0 = a.
 Existe un elemento 1 en K, diferente de 0, tal que para todo a en K, a · 1 = a
Existencia de elemento opuesto y de inversos:
 Para cada a en K, existe un elemento -a en K, tal que a + (- a) = 0.
 Para cada a ≠ 0 en K, existe un elemento a -1 en K, tal que a · a-1 = 1.
Distributividad de la multiplicación respecto de la adición
 Para toda a, b, c, en K, a · (b + c) = (a · b) + (a · c).

20. CUERPO: EJEMPLO 1
 Los números racionales Q = a b | a,
b con Z, b diferentes de 0 donde está
incluido el conjunto Z de los
números enteros.
 Es un cuerpo ya que tanto para la
suma como para multiplicación, son
cerradas para con la conmutación,
asociación, distribución, y hay
elemento neutro e inverso.

21. CUERPO: EJEMPLO 2
 Más generalmente, para un número
primo p, el conjunto de los números
enteros módulo p es un cuerpo finito con
los p elementos: esto se escribe a
menudo como Zp = { 0, 1,...,p-1} donde
las operaciones son definidas realizando
la operación en Z, dividiendo por p y
tomando el resto.