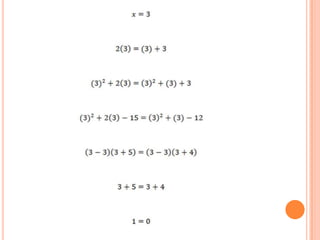Este documento presenta un problema matemático falaz que intenta demostrar que 1 es igual a 0 a través de una serie de pasos algebraicos. Sin embargo, al sustituir valores y aplicar propiedades matemáticas como la ley de sustitución y las propiedades de igualdad, se demuestra que el quinto paso del problema no es válido, rompiendo la igualdad y revelando el error en la demostración planteada.

1. Ana Cristina Ramos Alvarado
Héctor García Cárdenas
Alfredo Gutiérrez De la Fuente
1”B”
Lic. Gerardo Edgar Mata

2. Una demostración es una prueba de
que algo es verdadero. En
matemáticas es un argumento
deductivo para una afirmación
matemática la siguiente secuencia de
pasos algebraicos es una
demostración, desde luego falaz y
sofista de que uno es igual a cero

3. Demostración A

4.  Lógica Aristotélica: La lógica no es una ciencia, si no
un instrumento para el pensamiento correcto. De esta
manera es posible distinguir entre argumentos sólidos o
falsos y que no se nos induzca a engaños.
 Demostración: Razonamiento por lo cual se dan
pruebas de la exactitud de una proposición.
 Demostración matemática: Comprobar que es
coherente con las reglas lógicas que hacen funcionar
toda la teoría matemática y que no se contradice ninguna
otra afirmación que previamente se haya demostrado
que es cierta
 Argumento: Razonamiento que sirve para dar a conocer
las bases acerca del tema empleado

5.  Falaz: Razonamiento que no es valido.
 Sofista: Grupo de intelectuales que se dedicaban a la
enseñanza, pero este grupo tomo otro rumbo, pues se
aprovecharon de la ignorancia de la sociedad para sacar
algún beneficio
 Deductivo-Inductivo: La deducción va de lo general a lo
particular y la inducción de lo particular a lo general
 Afirmación matemática: Es un argumento deductivo
que se usa otras afirmaciones previamente establecidas
tales como teoremas.
 Operaciones algebraicas: una operación algebraica es
aquella en la que intervienen términos algebraicos.
Un término algebraico consta de;
Signo, coeficiente, literales y exponentes.

6.  Productos notables y factorización: Productos
notables es el nombre que reciben aquellos algoritmos
algebraicos cuya aplicación simplifica y sistematiza la
resolución de muchas operaciones habituales. La
factorización puede considerarse como la operación
inversa a la multiplicación, pues el propósito de ésta
última es hallar el producto de dos o más factores;
mientras que en la factorización, se buscan los factores
de un producto dado.
 Propiedades de la igualdad: Cuando se habla de
matemáticas se establece una comparación de valores
representado por el signo igual que es lo que separa al
primer miembro del segundo

9.  En esta serie de ecuaciones el valor que se le da a la
incógnita es 3, por lo que vamos a sustituir cada una de
las incógnitas.
 Después en la tercera operación recordando que se
sustituye “x” y elevar al cuadrado se hace la operación
pertinente, y el resultado de los dos miembros es 15 y
en la cuarta se hará lo mismo solo que aquí se le
restara un numero natural y el resultado que nos dará
es 0 en ambos miembros.
 Se inicia sumando y restando cada miembro, el
resultado de los dos términos del primer miembro se
multiplican, lo mismo se hace con los términos del
segundo miembro, el resultado también cumple con la
igualdad que es 0.
 En la quinta ecuación no cumple con la igualdad
requerida ya que sustituyendo y haciendo el
procedimiento los resultados de los dos miembros son 8
y 7 por lo que no son iguales

10. ERROR!

11. CUAL ES LA RELACIÓN DE LOS
CONCEPTOS CON EL
PROBLEMA?
 DEMOSTRACION: Utilizamos pruebas para
demostrar el error en el problema tal tales como el
empleo de la ley de sustitución y elevación al
cuadrado

12.  DEMOSTRACION MATEMATICA: Para demostrar
que el problema era incorrecto utilizamos y
seguimos leyes previamente establecidas, como un
argumento deductivo, como por ejemplo la
sustitución

13.  ARGUMENTO: Para demostrar que estábamos en
lo correcto debíamos tener argumentos validos y
esos argumentos eran los teoremas o leyes ya
establecidas como las propiedades de igualdad

14.  FALAZ y SOFISTA: El problema se podría decir
que es falaz y sofista ya que ha simple vista parece
estar correcto pero al revisarlo mas afondo es
incorrecto

15.  OPERACIONES ALGEBRAICAS BASICAS: El
problema que nos presentan es una simple
operación de algebra elemental

16.  PRODUCTOS NOTABLES Y FACTORIZACION:
Tiene relación en que la operación se realice asta
su mas mínima expresión.

17.  PROPIEDADES DE LA IGUALDAD: Se relaciona
por que el problema trata de dos objetos
matemáticos que se consideran iguales y esta
compuesta por el miembro izquierdo, símbolo de la
igualdad y miembro derecho.