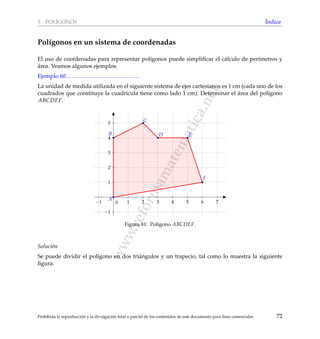
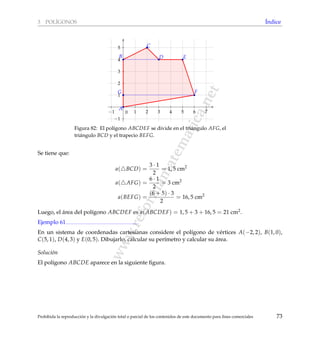
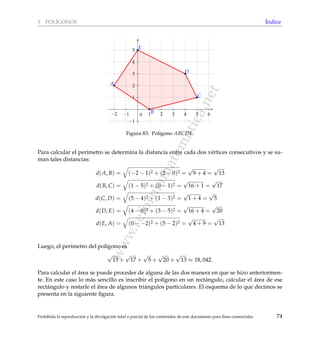
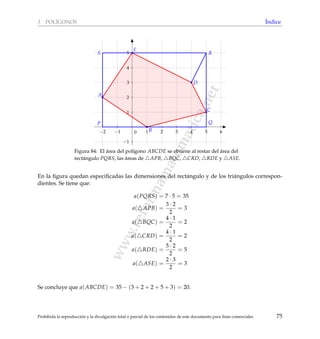
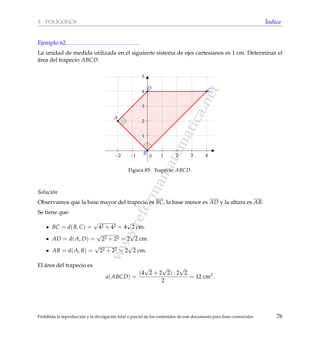
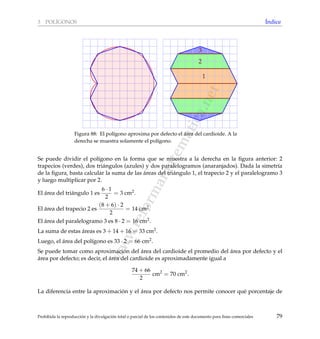
Este documento presenta un glosario matemático destinado a apoyar la preparación de estudiantes para los exámenes de bachillerato en matemáticas. Explica conceptos y resultados relacionados con geometría, incluyendo circunferencias, polígonos, transformaciones en el plano y visualización espacial. El material se organiza por temas y contiene índices alfabéticos para facilitar la búsqueda de contenidos específicos.






















































































![4 TRANSFORMACIONES EN EL PLANO ´Indice
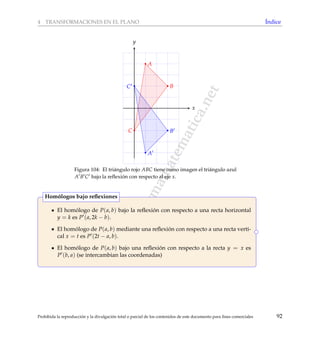
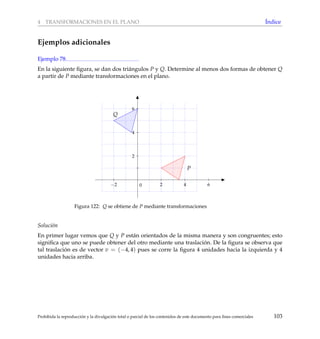
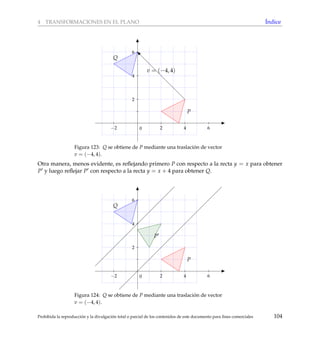
De hecho, toda traslaci´on es equivalente a la composici´on de dos reflexiones de
manera an´aloga a como se hizo en el ejemplo anterior.
Nota
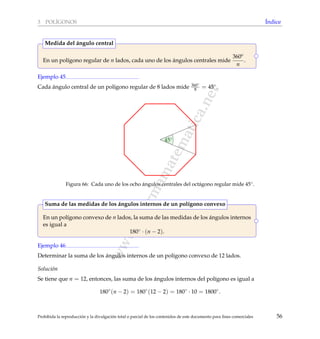
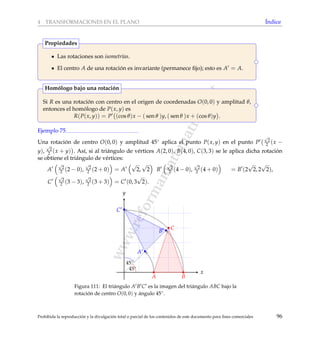
Ejemplo 79
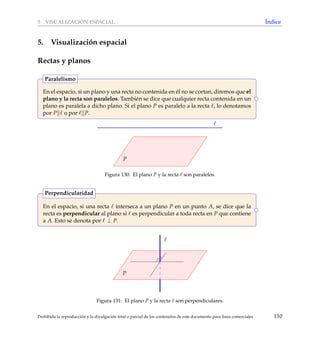
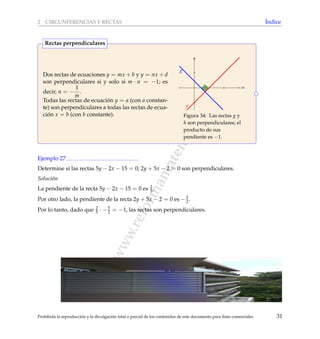
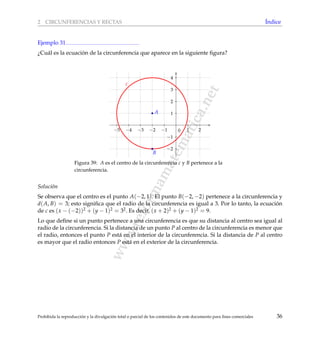
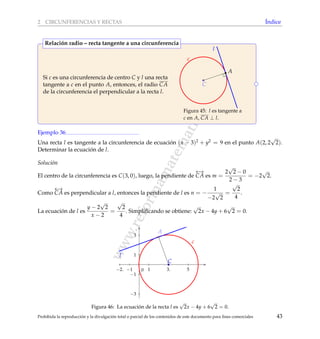
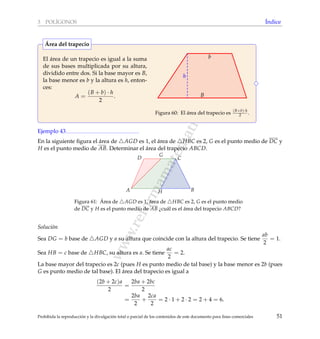
[Seleccionar la respuesta correcta] En la siguiente figura, el cuadril´atero P se obtiene del cuadril´ate-
ro Q mediante la aplicaci´on de una homotecia con centro en A y raz´on k.
A
P
Q
Figura 125: P se obtiene de Q mediante una homotecia.
Podemos asegurar que
A) k < −1
B) −1 < k < 0
C) 0 < k < 1
D) 1 < k
Soluci´on
Se observa que la imagen es de mayor tama˜no que la original por lo que |k| > 1. Por otra parte, el
centro de la homotecia est´a entre ambas figuras por lo que k es negativo. Se concluye que k < −1.
Prohibida la reproducci´on y la divulgaci´on total o parcial de los contenidos de este documento para fines comerciales 105](https://image.slidesharecdn.com/matcomplementariogeometria-180706035622/85/Material-complementario-geometria-107-320.jpg)