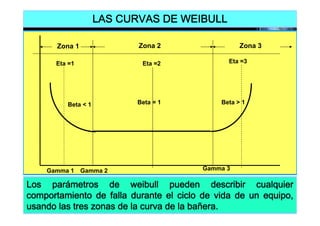
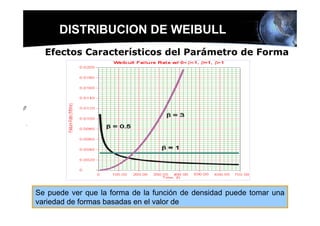
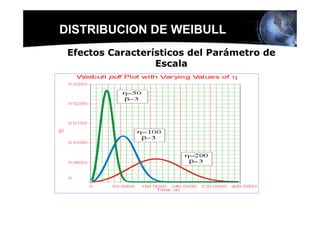
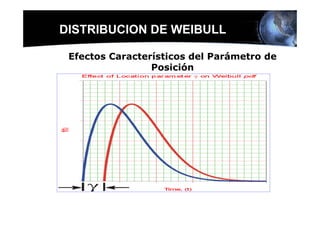
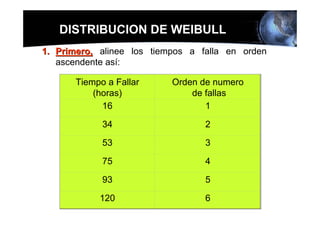
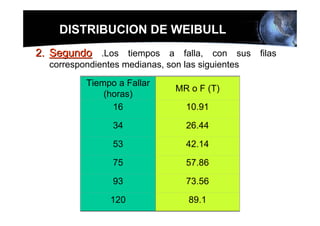
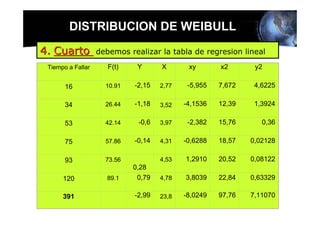
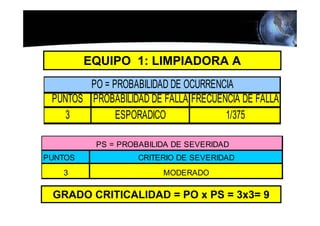
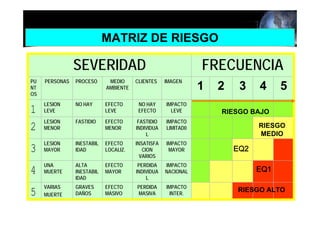
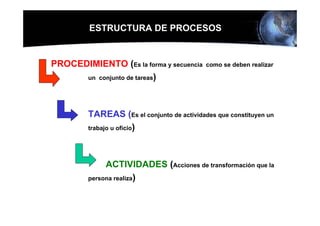
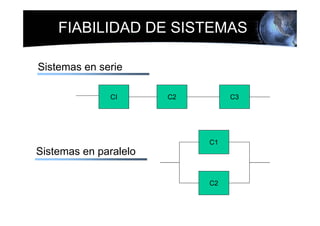
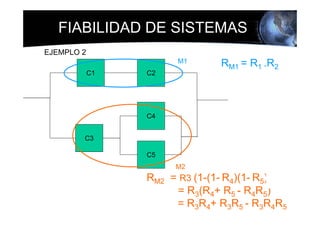
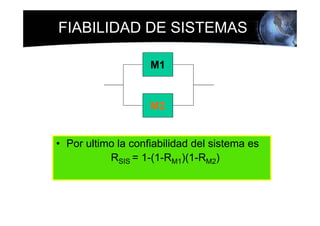
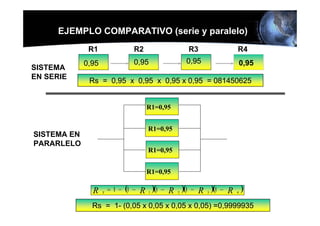
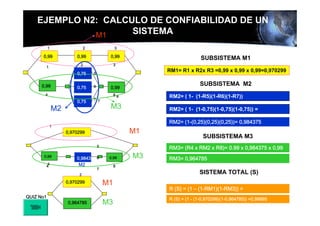
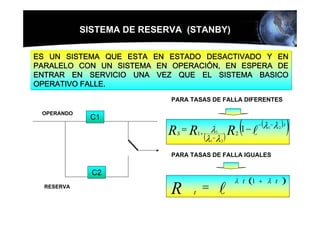
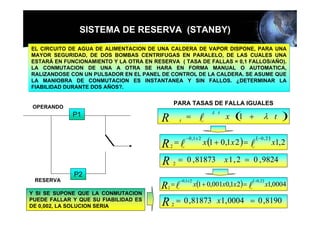
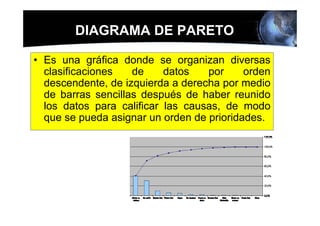
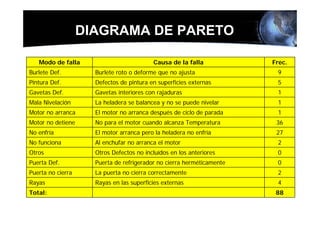
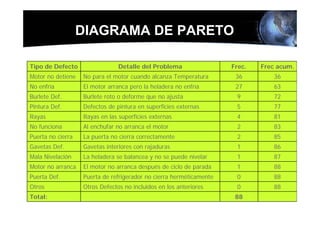
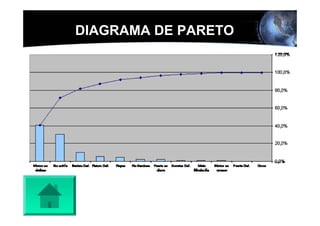
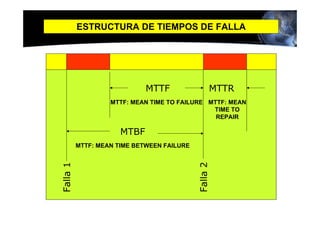
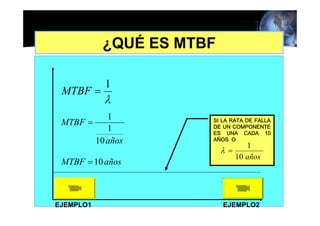
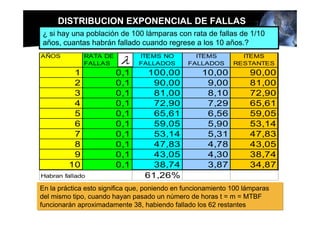
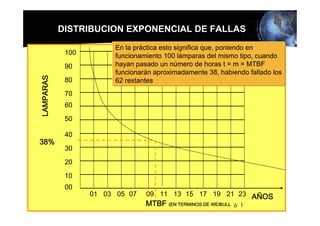
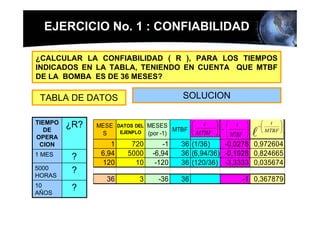
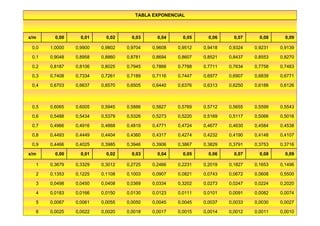
Este documento presenta los conceptos básicos de la confiabilidad aplicada a sistemas, incluyendo la definición de componente, equipo y sistema. Explica los diferentes tipos de sistemas (serie y paralelo) y cómo calcular su confiabilidad. También introduce conceptos como el diagrama de Pareto y distribuciones de probabilidad comúnmente usadas en confiabilidad como la binomial y de Poisson.

1. ESTADÍSTICA
APLICADA EN
CONFIABILIDAD

2. CONTENIDO
• CONFIABILIDAD BASICA
• FIABILIDAD EN SISTEMAS
• DIAGRAMA DE PARETO
• DISTRIBUCION BINOMIAL
• DISTRIBUCION DE POISSON
• DISTRIBUCION DE WEIBULL

3. CONFIABILIDAD
BASICA

4. COMPONENTE, EQUIPO, SISTEMA
COMPONENTE
DEFINIDO COMO LA PARTE PEQUEÑA DE UN ENSAMBLE.
EJEMPLOS: UN RESORTE, UN TORNILLO, UN PIÑON, UNA
BALINERA, ETC.
EQUIPO
DEFINIDO COMO UN CONJUNTO DE COMPONENTES
INTEGRADOS EN UNA FUNCION PREVIAMENTE DEFINIDA.
EJEMPLOS : BOMBAS, MOTORES, LICUADORAS, ETC.
SISTEMA
DEFINIDO COMO UN CONJUNTO EQUIPOS QUE EN SU
INTEGRIDAD PRESTA UN A FUNCION ESPECIFICA. EJEMPLO:
FUNCION DE BOMBEO( MOTOR + BOMBA), ETC.

5. ESTRUCTURA DE PROCESOS
MEGAPROCESOS PROCESOS
CENTRALES
MACROPROCESO
PROCESOS
SUBPROCESOS
PROCEDIMIENTOS
TAREAS
ACTIVIDADES

6. ESTRUCTURA DE PROCESOS
PROCEDIMIENTO (Es la forma y secuencia como se deben realizar
un conjunto de tareas)
TAREAS (Es el conjunto de actividades que constituyen un
trabajo u oficio)
ACTIVIDADES (Acciones de transformación que la
persona realiza)

7. FIABILIDAD DE SISTEMAS
Sistemas en serie
CI C2 C3
C1
Sistemas en paralelo
C2

8. FIABILIDAD DE SISTEMAS
Sistemas en serie
R ( s ) ( t ) = ψ ( R1 ( t ),..., R k ( t ))
k
= ∏ R (t )
i =1
i
Sistemas en paralelo
k
R ( p)
(t ) = 1 − ∏ (1 − Ri (t ))
i =1

9. COMPONENTE, EQUIPO, SISTEMA
PARA ENCONTRAR LA CONFIABILIDAD DE UN SISTEMA (Rs ),
EN SERIE, SE HACE NECESARIO ENCONTRAR EL
PRODUCTO DE LAS CONFIABILIDADES INDIVIDUALES DE
SUS COMPONENTES.
R1 = CONFIABILIDAD DEL COMPONENTE 1
R2 = CONFIABILIDAD DEL COMPONENTE 2
Rn = CONFIABILIDAD DEL COMPONENTE
Rs = R1 X R2 X R3 X........................Rn

10. MEDICION DE LA CONFIABILIDAD
EJEMPLO No3: Nels Electric, COLORADO, PRODUCE UN
SWITHC REVELADOR ELECTRICO, QUE TIENE TRES
COMPONENTES DISPUESTOS EN SERIE:
R1 R2 R3
0,90 0,80 0,99 Rs
Rs = 0,90 x 0,80 x 0,99 = 0,713 ( 71% )

11. FIABILIDAD DE SISTEMAS
EJEMPLO 1:
Una tarjeta de computadora tiene 200 componentes que deben
funcionar en forma correcta. La confiabilidad de cada componente,
para un periodo de 200 hr de funcionamiento, es R=0.9999.
¿Cual es la confiabilidad de la tarjeta para este
intervalo?
to = 200 hr
R (t o ) = (0.9999 )
(s)
sis
200
= 0.9802

12. FIABILIDAD DE SISTEMAS
• ¿Que pasaría si cada uno de los componentes
tuviera una confiabilidad de 0.99?
R (t o ) = (0.99 )
(s)
sis
200
= 0.134

13. FIABILIDAD DE SISTEMAS
EJEMPLO 2
M1 RM1 = R1 .R2
C1 C2
C4
C3
C5
M2
RM2 = R3 (1-(1- R4)(1- R5)) R3
= R3(R4+ R5 - R4R5)
= R3R4+ R3R5 - R3R4R5

14. FIABILIDAD DE SISTEMAS
M1
M2
• Por ultimo la confiabilidad del sistema es
RSIS = 1-(1-RM1)(1-RM2)

15. EJEMPLO COMPARATIVO (serie y paralelo)
R1 R2 R3 R4
0,95 0,95 0,95 0,95
SISTEMA
EN SERIE
Rs = 0,95 x 0,95 x 0,95 x 0,95 = 081450625
R1=0,95
R1=0,95
SISTEMA EN
PARARLELO
R1=0,95
R1=0,95
R S
= 1− ( −
1 R )(1 − R )(1 − R )(1
1 2 3
− R )
4
Rs = 1- (0,05 x 0,05 x 0,05 x 0,05) =0,9999935

16. EJEMPLO N2: CALCULO DE CONFIABILIDAD DE UN
M1 SISTEMA
1 2 3
0,99 0,99 0,99 SUBSISTEMA M1
2 3
1
RM1= R1 x R2x R3 =0,99 x 0,99 x 0,99=0,970299
0,75 5
0,99 6
SUBSISTEMA M2
0,75 0,99
4 88
7 7
RM2= ( 1- (1-R5)(1-R6)(1-R7))
0,75
M2 M3 RM2= ( 1- (1-0,75)(1-0,75)(1-0,75)) =
RM2= (1-(0,25)(0,25)(0,25))= 0,984375
1
0,970299 M1
SUBSISTEMA M3
5 RM3= (R4 x RM2 x R8)= 0.99 x 0,984375 x 0,99
0,99
0,9843 6 0,99 M3 RM3= 0,964785
4
4 M2 8
0,7 7
52
SISTEMA TOTAL (S)
0,970299 M1
R (S) = (1 – (1-RM1)(1-RM3)) =
QUIZ No1 R (S) = (1 - (1-0,970299)(1-0,964785)) =0,99895
0,964785 M3

17. SISTEMA DE RESERVA (STANBY)
ES UN SISTEMA QUE ESTA EN ESTADO DESACTIVADO Y EN
PARALELO CON UN SISTEMA EN OPERACIÓN, EN ESPERA DE
ENTRAR EN SERVICIO UNA VEZ QUE EL SISTEMA BASICO
OPERATIVO FALLE.
PARA TASAS DE FALLA DIFERENTES
OPERANDO
C1
RS = R1+ λ1(λ −λ )R
(1 − l (λ λ ) )
2
− 1
− 2
.t
1 2
PARA TASAS DE FALLA IGUALES
C2
λ t (1 + λ t )
RESERVA
R t
= l

18. SISTEMA DE RESERVA (STANBY)
EL CIRCUITO DE AGUA DE ALIMENTACION DE UNA CALDERA DE VAPOR DISPONE, PARA UNA
MAYOR SEGURIDAD, DE DOS BOMBAS CENTRIFUGAS EN PARALELO, DE LAS CUALES UNA
ESTARÁ EN FUNCIONAMIENTO Y LA OTRA EN RESERVA ( TASA DE FALLAS = 0,1 FALLOS/AÑO).
LA CONMUTACION DE UNA A OTRA SE HARA EN FORMA MANUAL O AUTOMATICA,
RALIZANDOSE CON UN PULSADOR EN EL PANEL DE CONTROL DE LA CALDERA. SE ASUME QUE
LA MANIOBRA DE CONMUTACION ES INSTANTANEA Y SIN FALLOS. ¿DETERMINAR LA
FIABILIDAD DURANTE DOS AÑOS?.
PARA TASAS DE FALLA IGUALES
OPERANDO
P1
R t
= l
λ t
x (1 + λ t )
(−0 , 2 )
x (1 + 0 ,1 x 2 ) = l
− 0 ,1 x 2
R2 = l x1, 2
R 2
= 0 , 81873 x 1 , 2 = 0 , 9824
P2
( −0, 2 )
x(1 + 0,001x0,1x 2) = l
RESERVA −0 ,1 x 2
R2 = l x1,0004
Y SI SE SUPONE QUE LA CONMUTACION
PUEDE FALLAR Y QUE SU FIABILIDAD ES
R 2
= 0 ,81873 x1, 0004 = 0 ,8190
DE 0,002, LA SOLUCION SERIA

19. DIAGRAMA DE PARETO
Principio de Pareto (pocos vitales, muchos triviales)
Detectar los problemas que tienen más relevancia
Ya que por lo general, el 80% de los resultados
totales se originan en el 20% de los elementos.

20. DIAGRAMA DE PARETO
Ejemplo de Minorías vitales:
– La minoría de clientes que representen
la mayoría de las ventas.
– La minoría de problemas causantes del
grueso del retraso de un proceso.
– La minoría de personas que controlan la
mayoría de dinero en un país.

21. DIAGRAMA DE PARETO
• Es una gráfica donde se organizan diversas
clasificaciones de datos por orden
descendente, de izquierda a derecha por medio
de barras sencillas después de haber reunido
los datos para calificar las causas, de modo
que se pueda asignar un orden de prioridades.

22. DIAGRAMA DE PARETO
• El Dr. Juran aplicó este concepto a la calidad,
obteniéndose lo que hoy se conoce como la
regla 80/20.
• Según este concepto, si se tiene un problema
con muchas causas, podemos decir que el
20% de las causas resuelven el 80% del
problema y el 80% de las causas solo
resuelven el 20% del problema.

23. DIAGRAMA DE PARETO
Para que se utiliza:
• Para analizar las causas
• Para estudiar los resultados
• Para planear una mejora continua
• Las Gráficas de Pareto son especialmente
valiosas como fotos de “antes y después”
para demostrar qué progreso se ha
logrado.

24. DIAGRAMA DE PARETO
Pasos para llevar a cabo este diagrama:
• Determinar los datos a reunir (diseño de la investigación).
• Recoger los datos.
• Organización de los datos (tablas de frecuencia, graficas,
etc.)
• Calcular índices que permitan resumir los datos
recolectados.
• Analizar y evaluar la información.
• Tomar de decisiones.
• Controlar los cambios realizados.

25. DIAGRAMA DE PARETO
Ejemplo:
• Un fabricante de heladeras desea
analizar cuales son los defectos más
frecuentes que aparecen en las
unidades al salir de la línea de
producción.

26. DIAGRAMA DE PARETO
Modo de falla Causa de la falla Frec.
Burlete Def. Burlete roto o deforme que no ajusta 9
Pintura Def. Defectos de pintura en superficies externas 5
Gavetas Def. Gavetas interiores con rajaduras 1
Mala Nivelación La heladera se balancea y no se puede nivelar 1
Motor no arranca El motor no arranca después de ciclo de parada 1
Motor no detiene No para el motor cuando alcanza Temperatura 36
No enfría El motor arranca pero la heladera no enfría 27
No funciona Al enchufar no arranca el motor 2
Otros Otros Defectos no incluídos en los anteriores 0
Puerta Def. Puerta de refrigerador no cierra herméticamente 0
Puerta no cierra La puerta no cierra correctamente 2
Rayas Rayas en las superficies externas 4
Total: 88

27. DIAGRAMA DE PARETO
Tipo de Defecto Detalle del Problema Frec. Frec acum.
Motor no detiene No para el motor cuando alcanza Temperatura 36 36
No enfría El motor arranca pero la heladera no enfría 27 63
Burlete Def. Burlete roto o deforme que no ajusta 9 72
Pintura Def. Defectos de pintura en superficies externas 5 77
Rayas Rayas en las superficies externas 4 81
No funciona Al enchufar no arranca el motor 2 83
Puerta no cierra La puerta no cierra correctamente 2 85
Gavetas Def. Gavetas interiores con rajaduras 1 86
Mala Nivelación La heladera se balancea y no se puede nivelar 1 87
Motor no arranca El motor no arranca después de ciclo de parada 1 88
Puerta Def. Puerta de refrigerador no cierra herméticamente 0 88
Otros Otros Defectos no incluidos en los anteriores 0 88
Total: 88

28. DIAGRAMA DE PARETO

29. MEDICION DE LA CONFIABILIDAD
PARA CREAR UN MODELO MATEMÁTICO PARA LA
PROBABILIDAD DE FALLO, CONSIDERAMOS EL
FUNCIONAMIENTO DE UN DETERMINADO ELEMENTO EN EL
MEDIO PARA ÉL ESPECIFICADO. DEFINIMOS LA VARIABLE
ALEATORIA COMO EL TIEMPO DURANTE EL QUE EL ELEMENTO
FUNCIONA SATISFACTORIAMENTE ANTES DE QUE SE
PRODUZCA UN FALLO.
LA PROBABILIDAD DE QUE EL ELEMENTO PROPORCIONE UNOS
RESULTADOS SATISFACTORIOS EN EL MOMENTO T SE PUEDE
DEFINIR COMO FIABILIDAD. LA DESIGNAMOS R (T)

30. MEDICION DE LA CONFIABILIDAD
DE UNA FORMA PRÁCTICA SI DESIGNAMOS:
NS (T) = Nº DE ELEMENTOS EN FUNCIONAMIENTO EN EL INSTANTE T
N (0) = Nº DE ELEMENTOS EN FUNCIONAMIENTO AL PRINCIPIO
NF (T) = Nº DE ELEMENTOS AVERIADOS HASTA EL MOMENTO T
SE CUMPLIRÁ:
N (0) = NF (T) + NS (T)

31. MEDICION DE LA CONFIABILIDAD
LA FIABILIDAD R (T) ESTÁ RELACIONADA CON LA FUNCIÓN
INVERSA LLAMADA INFIABILIDAD Q (T) QUE ES SU
PROBABILIDAD CONTRARIA O SEA LA PROBABILIDAD DE QUE
OCURRA UN FALLO ANTES DEL INSTANTE T.
POR LO TANTO LA INFIABILIDAD VALDRÁ:
−t
R (t ) = l m
CUMPLIÉNDOSE QUE: la no confiabilidad Q(T)
Q (T) = 1 - R (T) (4)

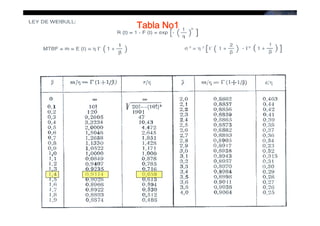
32. MEDICION DE LA CONFIABILIDAD
Q[ ] =1− R( )t t
−t
R (t ) = l m
−t
R( ) =l t
m

33. MEDICION DE LA CONFIABILIDAD
FALLA: ES EL CAMBIO EN UN PRODUCTO O SISTEMA DESDE UNA
CONDICION SATISFACTORIA ( ESTANDAR ) DE TABRAJO, A UNA
CONDICION DE TRABAJO POR DEBAJO DEL ESTANDAR.
LA UNIDAD BASICA DE MEDIDA PARA CONFIABILIDAD ES LA TASA DE
FALLA DEL PRODUCTO (FR) . LA TASA DE FALLA MIDE EL PORCENTAJE
DE FALLAS ENTRE EL NUMERO TOTAL DE PRODUCTOS PROBADOS, O
DE UN NUMERO DE FALLAS DURANTE UN PERIDO DE TIEMPO, ( FR (N) ).
FR (%) = NUMERO DE FALLAS / NUMERO DE UNIDADES PROBADAS
FR (N ) = NUMERO DE FALLAS / UNIDADES DE TIEMPO DE OPERACION
QUIZAS EL TERMINO MAS COMUN EN EL ANALISIS DE CONFIABILIDAD
ES EL TIEMPÓ PROMEDIO DE FALLA ( MTBF) QUE ES EL RECIPROCO
DE FR(N).
FR ( N ) = λ MTBF = 1 / FR (N)

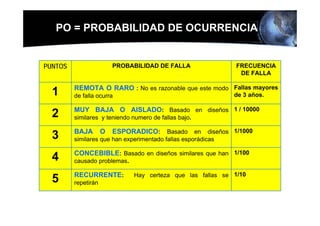
34. MEDICION DE LA CONFIABILIDAD
EJEMPLO No2: VEINTE SISTEMAS DE AIRE ACONDICIONADOS, QUE SERAN
UTILIZADOS POR ASTRONAUTAS DE LA NASA EN LOS TRANSBORDADORES,
FUERON OPERADOS DURANTE 1000 HORAS, EN LAS INSTALACIONES DE PRUEBA
DE LA NASA EN HUNTSVILLE, ALABAMA. DOS DE LOS SISTEMAS FALLARON
DURANTE LA PRUEBA, UNO DESPUES DE LAS 200 HORAS Y EL OTRO DESPUES
DE LAS 600 HORAS. 1. CUAL ES EL PORCENTAJE DE FALLAS?. 2.CUAL ES EL
NUMERO DE FALLAS POR TIEMPO DE OPERACIÓN? 3. CALCULE EL TIEMPO
PROMEDIO DE FALLAS?
1.FRECUENCIA DE FALLA FR(%) = NUMERO DE FALLAS/ No UNIDADES
PROBADAS DE DONDE FR( % ) = 2/20 = 0,10 O 10 %
2. No FALLAS POR HORA DE OPERACIÓN:
FR( N) = NUMERO DE FALLAS/TIEMPO DE OPERACIÓN DE DONDE
FR( N ) = 2 / TIEMPO TOTAL OPERACIÓN - TIEMPO PERDIDO
REMPLAZANDO FR ( N) = 2/ (1000x 20) – [( 800 hrs . 1 falla) + (400 hrs. 2
falla)]
RESULTADO FR ( N ) = 2 fallas/ 18800 hrs = 0,000106 UNIDADES HORA
POR OTRA PARTE : MTBF = 1 / FR(N) = 1/ 0,000106 = 9434 hrs

35. MEDICION DE LA CONFIABILIDAD
EJEMPLO2: VEINTE SISTEMAS DE AIRE ACONDICIONADOS,
QUE SERAN UTILIZADOS POR ASTRONAUTAS DE LA NASA EN
LOS TRANSBORDADORES, FUERON OPERADOS DURANTE 1000
HORAS, EN LAS INSTALACIONES DE PRUEBA DE LA NASA EN
HUNTSVILLE, ALABAMA. DOS DE LOS SISTEMAS FALLARON
DURANTE LA PRUEBA, UNO DESPUES DE LAS 200 HORAS Y EL
OTRO DESPUES DE LAS 600 HORAS.
3. SI EL VIAJE TIPICO DEL TRASBORDADOR DURA 60 DIAS , LA
NASA ESTA INTERESADA EN CONOCER CUAL ES LA TASA DE
FALLA POR VIAJE?:
TASA DE FALLA = ( No.FALLAS/HORA) X (UNIDADES) X ( TOTAL
HORAS DE OPERACIÓN
TASA DE FALLAS = ( 0,000106 ) ( 24 hrs / dia X 60 dias / viaje)
TASA DE FALLAS = 0,000106 x 24 x 60
TASA DE FALLAS = 0,152 FALLAS POR VIAJE

36. CONFIABILIDAD BASICA
TASA INSTANTÁNEA DE FALLA
f (t ) λ(t) es la frecuencia con que
λ (t ) =
R (t ) se presentan los fallos en
t los componentes,
R (t ) = e ∫o λ ( t ). dt
−
expresada en fallos/hora.
La inversa de λ(t), 1/λ(t) (horas/fallo) es el denominado
MTBF (Mean Time Between Failures, Tiempo Medio
Entre Fallos).

37. ESTRUCTURA DE TIEMPOS DE FALLA
MTTF MTTR
MTTF: MEAN TIME TO FAILURE MTTF: MEAN
TIME TO
REPAIR
MTBF
MTTF: MEAN TIME BETWEEN FAILURE
Falla 2
Falla 1

38. ¿QUÉ ES MTBF
1
MTBF =
λ
1
MTBF = SI LA RATA DE FALLA
1 DE UN COMPONENTE
ES UNA CADA 10
10 años AÑOS O
1
λ=
10 años
MTBF = 10 años
EJEMPLO1 EJEMPLO2

39. DISTRIBUCION EXPONENCIAL DE FALLAS
¿ si hay una población de 100 lámparas con rata de fallas de 1/10
años, cuantas habrán fallado cuando regrese a los 10 años.?
AÑOS RATA DE
FALLAS λ ITEMS NO
FALLADOS
ITEMS
FALLADOS
ITEMS
RESTANTES
1 0,1 100,00 10,00 90,00
2 0,1 90,00 9,00 81,00
3 0,1 81,00 8,10 72,90
4 0,1 72,90 7,29 65,61
5 0,1 65,61 6,56 59,05
6 0,1 59,05 5,90 53,14
7 0,1 53,14 5,31 47,83
8 0,1 47,83 4,78 43,05
9 0,1 43,05 4,30 38,74
10 0,1 38,74 3,87 34,87
Habran fallado 61,26%
En la práctica esto significa que, poniendo en funcionamiento 100 lámparas
del mismo tipo, cuando hayan pasado un número de horas t = m = MTBF
funcionarán aproximadamente 38, habiendo fallado los 62 restantes

40. DISTRIBUCION EXPONENCIAL DE FALLAS
En la práctica esto significa que, poniendo en
100 funcionamiento 100 lámparas del mismo tipo, cuando
90 hayan pasado un número de horas t = m = MTBF
funcionarán aproximadamente 38, habiendo fallado los
LAMPARAS
80 62 restantes
70
60
50
40
38%
30
20
10
00
01 03 05 07 09 11 13 15 17 19 21 23 AÑOS
MTBF (EN TERMINOS DE WEIBULL η )

41. EJERCICIO No. 1 : CONFIABILIDAD
¿CALCULAR LA CONFIABILIDAD ( R ), PARA LOS TIEMPOS
INDICADOS EN LA TABLA, TENIENDO EN CUENTA QUE MTBF
DE LA BOMBA ES DE 36 MESES?
TABLA DE DATOS SOLUCION
TIEMPO ¿R? MESE DATOS DEL MESES ⎛
⎜
t ⎞ ⎛ t ⎞
⎟ −⎜ ⎟
⎛ t
−⎜
⎞
⎟
DE
OPERA
S EJENPLO (por -1)
MTBF
⎝ MTBF ⎠ ⎝ MTBF ⎠ l ⎝ MTBF ⎠
CION 1 720 -1 36 (1/36) -0,0278 0,972604
1 MES 6,94 5000 -6,94 36 (6,94/36) -0,1928 0,824665
?
120 10 -120 36 (120/36) -3,3333 0,035674
5000 ?
HORAS
36 3 -36 36 -1 0,367879
10 ?
AÑOS

42. TABLA EXPONENCIAL
x/m 0,00 0,01 0,02 0,03 0,04 0,05 0,06 0,07 0,08 0,09
0,0 1,0000 0,9900 0,9802 0,9704 0,9608 0,9512 0,9418 0,9324 0,9231 0,9139
0,1 0,9048 0,8958 0,8860 0,8781 0,8694 0,8607 0,8521 0,8437 0,8553 0,8270
0,2 0,8187 0,8106 0,8025 0,7945 0,7866 0,7788 0,7711 0,7634 0,7758 0,7483
0,3 0,7408 0,7334 0,7261 0,7189 0,7116 0,7447 0,6977 0,6907 0,6839 0,6771
0,4 0,6703 0,6637 0,6570 0,6505 0,6440 0,6376 0,6313 0,6250 0,6188 0,6126
0,5 0,6065 0,6005 0,5945 0,5886 0,5827 0,5769 0,5712 0,5655 0,5599 0,5543
0,6 0,5488 0,5434 0,5379 0,5326 0,5273 0,5220 0,5169 0,5117 0,5066 0,5016
0,7 0,4966 0,4916 0,4868 0,4819 0,4771 0,4724 0,4677 0,4630 0,4584 0,4538
0,8 0,4493 0,4449 0,4404 0,4360 0,4317 0,4274 0,4232 0,4190 0,4148 0,4107
0,9 0,4466 0,4025 0,3985 0,3946 0,3906 0,3867 0,3829 0,3791 0,3753 0,3716
x/m 0,00 0,01 0,02 0,03 0,04 0,05 0,06 0,07 0,08 0,09
1 0,3679 0,3329 0,3012 0,2725 0,2466 0,2231 0,2019 0,1827 0,1653 0,1496
2 0,1353 0,1225 0,1108 0,1003 0,0907 0,0821 0,0743 0,0672 0,0608 0,5500
3 0,0498 0,0450 0,0408 0,0369 0,0334 0,3202 0,0273 0,0247 0,0224 0,2020
4 0,0183 0,0166 0,0150 0,0130 0,0123 0,0111 0,0101 0,0091 0,0082 0,0074
5 0,0067 0,0061 0,0055 0,0050 0,0045 0,0045 0,0037 0,0033 0,0030 0,0027
6 0,0025 0,0022 0,0020 0,0018 0,0017 0,0015 0,0014 0,0012 0,0011 0,0010

43. EJEMPLO PRÁCTICO
DURANTE EL PROGRAMA DE MANTENIMIENTO ANUAL QUE
REALIZA UNA EMPRESA SE HAN RECOGIDO LOS DATOS DE FALLOS
DE UN CONJUNTO DE 50 VÁLVULAS MECÁNICAS HABIENDO
FALLADO 2 DE ELLAS. PARA REPROGRAMAR EL PROGRAMA DE
MANTENIMIENTO PREVENTIVO QUE SE LLEVA ACTUALMENTE EN
LA EMPRESA SE DESEA SABER:
1. TASA DE FALLOS ANUAL PARA DICHAS VÁLVULAS.
2. QUÉ PROBABILIDAD TIENE UNA VÁLVULA DE FALLAR ANTES DE
ALCANZAR UN TIEMPO DE FUNCIONAMIENTO DE 4 MESES.
3. CUÁL SERÁ LA PROBABILIDAD DE QUE LA UNA VÁLVULA ESTÉ
EN FUNCIONAMIENTO AL CABO DE 6 MESES.
4. CUÁL SERÁ LA PROBABILIDAD DE QUE EL TIEMPO DE VIDA
ESTÉ COMPRENDIDO ENTRE 4 Y 6 MESES.
5. DETERMINAR UN INTERVALO DE VIDA CON UN NIVEL DE
CONFIANZA (CENTRADO) DEL 90 %.

44. SOLUCION EJEMPLO PRÁCTICO
1. LA TASA DE FALLOS SERÁ LA RELACIÓN ENTRE EL NÚMERO DE VÁLVULAS
FALLADAS Y EL NÚMERO TOTAL DE VÁLVULAS EN FUNCIONAMIENTO:
2.
2. LA PROBABILIDAD DE QUE UNA VÁLVULA FALLE ANTES DE UN NÚMERO
LA PROBABILIDAD DE QUE UNA VÁLVULA FALLE ANTES DE UN NÚMERO
DETERMINADO DE MESES VIENE EXPRESADO POR LA INFIABILIDAD Q (T):
DETERMINADO DE MESES VIENE EXPRESADO POR LA INFIABILIDAD Q (T):
Q(t)= 1 - exp ( - λt)
λ= 4. 10-2
t = 4 meses - expresado en años = 1/3 año
Luego, para t = 1/3, se tendrá:
Q (t) = 1 - exp (- 4.10 -2 . 1/3) = 1 - 0,986886 = 0,013114

45. SOLUCION EJEMPLO PRÁCTICO
3. LA PROBABILIDAD DE QUE NO SE HAYA PRODUCIDO EL
FALLO ANTES DE LOS 6 MESES SERÁ LA FIABILIDAD PARA
ESE TIEMPO, QUE RESULTARÁ:
R (T) = EXP (-λT) = EXP (- 4. 10-2 . 1/2) = EXP (- 0,002) =
0,998
ESTO QUIERE DECIR QUE EXISTE UNA PROBABILIDAD
DEL 99,80 % DE QUE UNA VÁLVULA NO SE AVERÍE
ANTES DE LOS SEIS MESES.

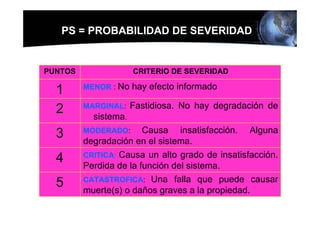
46. SOLUCION EJEMPLO PRÁCTICO
4. LA PROBABILIDAD DE QUE EL TIEMPO DE VIDA ESTÉ
COMPRENDIDO ENTRE 4 Y 6 MESES SERÁ LA DIFERENCIA
ENTRE LA PROBABILIDAD DE QUE FALLE ANTES DE LOS 6
MESES Y LA DE QUE FALLE ANTES DE LOS 4 MESES;
MATEMÁTICAMENTE SERÁ LA DIFERENCIA ENTRE LAS
INFIABILIDADES DE AMBOS PERIODOS DE TIEMPO SEA:
Pr = Q (1/2) - Q (1/3) =
=[1 - exp (- 1/2)] - [1 - exp (- 1/3)] =
=exp (- 1/3) - exp (-1/2) =
= 0,7165-0,6065= (11 %)

47. SOLUCION EJEMPLO PRÁCTICO
5. SUSTITUYENDO LAS EXPRESIONES LUEGO, DEBE VERIFICARSE
ANTERIORES POR SUS RESPECTIVOS QUE LOS VALORES DE LA
VALORES TENDREMOS:
INFIABILIDAD PARA LOS
1 - EXP (- T1) = 0,05
MOMENTOS T1, Y T 2 SERÁN
1 - EXP (-T2) = 0,95 RESPECTIVAMENTE:
DESPEJANDO:
Q (T1) = 0,05
EXP (- T1) = 0,95
EXP (- T2) = 0,05 Q (T2) = 0,95
INVIRTIENDO:
EXP (T1) = 1,06 DE DONDE T1 = 0,05826
AÑOS
EXP (T2) = 20 DE DONDE T2 = 2,9957
AÑOS
Luego, para un nivel de confianza del 90 %,
la vida de la válvula estará comprendida
entre 0,05826 y 2,9957 años.

48. DISTRIBUCION DE
WEIBULL

49. DISTRIBUCION DE WEIBULL
EL ANÁLISIS DEL WEIBULL DE DATOS DE FALLA ES
UNA HERAMIENTA IMPORTANTE DE LA
CONFIABILIDAD. LA DISTRIBUCIÓN DEL WEIBULL
FUE INVENTADA POR WALODDI WEIBULL EN LOS
AÑOS 1930. ES EL MODELO ESTADÍSTICO MÁS
POPULAR PARA LOS DATOS DE VIDA DE UN
EQUIPO.
WEIBULL TIENE LA VENTAJA DE USAR LOS
TAMAÑOS DE LA MUESTRA MUY PEQUEÑOS PARA
HACER JUICIOS RAZONABLE DE CONDUCTA
FUTURA DE VIDA DE LOS EQUIPOS

50. LAS CURVAS DE WEIBULL
Zona 1 Zona 2 Zona 3
Eta =1 Eta =2 Eta =3
Beta < 1 Beta = 1 Beta > 1
Gamma 1 Gamma 2 Gamma 3
Los parámetros de weibull pueden describir cualquier
comportamiento de falla durante el ciclo de vida de un equipo,
usando las tres zonas de la curva de la bañera.

51. DISTRIBUCION DE WEIBULL
La Distribución Weibull de Tres parámetros
γ
ETA η = Parámetro escalar.
BETA β = Parámetro de forma.
GAMMA γ = Parámetro de posición.

52. PARAMETROS DE LA DISTRIBUCION DE
WEIBULL
η ETA, LA CARACTERÍSTICA DE VIDA, O EL PUNTO A
QUE 63,2% DE LOS ITEMS PROBABLEMENTE
HABRÁN FALLADO CON EL MISMO MODO DE FALLA.
β
BETA, ES LA CUESTA DE LA CURVA O LA
CARACTERÍSTICA DE LA FORMA DE LA CURVA DE
FALLAS. LA BETA SE USA PARA AYUDAR A
DETERMINAR QUÉ CLASE DE ACTIVIDADES DE
MANTENIMIENTO SE DESTINA PARA UN MODO DE
FALLA DADO.
γ GAMMA DESCRIBE EL PUNTO A QUE LA
CURVA DE WEIBULL CAMBIA DE FORMA.

53. DISTRIBUCION DE WEIBULL
Efectos Característicos del Parámetro de Forma
.
Se puede ver que la forma de la función de densidad puede tomar una
variedad de formas basadas en el valor de

54. DISTRIBUCION DE WEIBULL
Efectos Característicos del Parámetro de
Escala

55. DISTRIBUCION DE WEIBULL
Efectos Característicos del Parámetro de
Posición

56. DISTRIBUCION DE WEIBULL
La ecuación para la función de densidad Weibull
acumulativa de tres parámetros, es dada por
El valor r(t), en el tiempo t, es la razón de falla
instantánea de los componentes que aun existen en el
periodo t

57. EJERCICIO No. 2 : CONFIABILIDAD
CUAL ES LA CONFIABILIDAD DE UN VENTILADOR
PARA UN TIEMPO DE OPERACIÓN DE 17.000 HORAS,
SI EL VENTILADOR TIENE UNA CARACTERISTICA DE
VIDA DE η DE 8760 HORAS Y BETA β ES DE 4,07
( )l
β
− ⎛ t ⎞ = 17000
4
− (1 , 94 )4
R (t ) = l ⎜ η ⎟ l
=
⎝ ⎠ 8760
−7
R ( t ) = 6 ,92 X 10

58. PROPIEDADES ESTADISITICAS DE
LA DISTRIBUCION DE WEIBULL
La Media o MTTF
La Desviación Estándar

59. REGRESION EN LA DISTRIBUCION
DE WEIBULL
Convertir la función en una forma lineal
x= Ln(T)
que causa la ecuación lineal de,

60. REGRESION EN LA DISTRIBUCION
DE WEIBULL
∑ x 2 ∑ y − ∑ x ∑ xy n∑ xy − ∑ x∑ y
a= b=β =
n∑ x − (∑ x ) n∑ x − (∑ x )
2 2 2 2
a
η = e −β

61. DESARROLLO DE LAREGRESION
EN LA DISTRIBUCION DE WEIBULL
Pasos para la regresión
1. Primero se alinea los tiempos de fallo en orden
ascendente
2. Segundo se Obtiene la mediana trazando
posiciones, mediante la siguiente ecuación:
donde i es el número de orden de fallos y N es el
tamaño total de la muestra.

62. DESARROLLO DE LAREGRESION
EN LA DISTRIBUCION DE WEIBULL
Pasos para la regresión
3. Tercero debemos hallar los Xi y Yi para poder aplicar
represión lineal mediante las siguientes ecuaciones:

63. DESARROLLO DE LAREGRESION
EN LA DISTRIBUCION DE WEIBULL
Pasos para la regresión
4. Cuarto debemos realizar la tabla de regresion lineal
Tiempo de F(T) x y xy x2 y2
falla

64. DESARROOLLO DE LAREGRESION
EN LA DISTRIBUCION DE WEIBULL
Pasos para la regresión
5. Quinto debemos hallar a y b
a=
∑ x 2 ∑ y − ∑ x ∑ xy
b=β =
n∑ xy − ∑ x∑ y
n∑ x − (∑ x ) n∑ x − (∑ x )
2 2 2
2
Donde a
η=e −β

65. DESARROOLLO DE LAREGRESION
EN LA DISTRIBUCION DE WEIBULL
Pasos para la regresión
6. Sexto se puede hallar la confiabilidad o razón de falla
instantánea de los componentes

66. DISTRIBUCION DE WEIBULL
EJEMPLO:
Asuma que seis unidades idénticas con la fiabilidad
probada en la misma aplicación y niveles de tensión de
operación. Todas estas unidades fallan durante la prueba
después de haber funcionado el número siguiente de horas
: 93, 34, 16, 120, 53 y 75. Estime los valores de los
parámetros para una distribución Weibull de dos
parámetros y determine la fiabilidad de las unidades a la 15
horas puesto a operar 1 semana después de haber sido
compradas

67. DISTRIBUCION DE WEIBULL
1. Primero, alinee los tiempos a falla en orden
ascendente así:
Tiempo a Fallar Orden de numero
(horas) de fallas
16 1
34 2
53 3
75 4
93 5
120 6

68. DISTRIBUCION DE WEIBULL
2. Paso : Se Obtiene la mediana trazando posiciones,
mediante la siguiente ecuación:
donde i es el número de orden de fracaso y N es el tamaño
total de la muestra.
MR% = (1 – 0.3 / 6 + 0.4) *100
MR% = 10.91

69. DISTRIBUCION DE WEIBULL
2. Segundo .Los tiempos a falla, con sus filas
correspondientes medianas, son las siguientes
Tiempo a Fallar
MR o F (T)
(horas)
16 10.91
34 26.44
53 42.14
75 57.86
93 73.56
120 89.1

70. Tamaño de muestra
N
u
m
e
r
o
d
e
f
a
ll
o
s

71. DISTRIBUCION DE WEIBULL
3. Tercero: Luego debemos hallar los Xi y Yi para poder
aplicar regresión lineal mediante las siguientes ecuaciones:
Yi = ln ( -ln (1 - 0.1091))
Y1 =2,15
X1 = ln 16
X1 = 2.77

72. DISTRIBUCION DE WEIBULL
3. Tercero: Luego debemos hallar los Xi y Yi para poder
aplicar regresión lineal mediante las siguientes ecuaciones:
Yi = ln ( -ln (1 - 0.2644))
Y1 = -1,18
X1 = ln 34
X1 = 3,52

73. DISTRIBUCION DE WEIBULL
4. Cuarto debemos realizar la tabla de regresion lineal
Tiempo a Fallar F(t) Y X xy x2 y2
16 10.91 -2,15 2,77 -5,955 7,672 4,6225
34 26.44 -1,18 3,52 -4,1536 12,39 1,3924
53 42.14 -0,6 3,97 -2,382 15,76 0,36
75 57.86 -0,14 4,31 -0,6288 18,57 0,02128
93 73.56 4,53 1,2910 20,52 0,08122
0,28
120 89.1 0,79 4,78 3,8039 22,84 0,63329
391 -2,99 23,8 -8,0249 97,76 7,11070

74. DISTRIBUCION DE WEIBULL
Luego a través de las ecuaciones de Represión hallamos
ayb
a=
∑ x 2 ∑ y − ∑ x∑ xy
n∑ x − (∑ x)
2 2
(97.76 * −2.99) − (23.88 * −8.0249)
a= = −6.15
6(97.7696 − (23.88 ))
2
n ∑ xy − ∑ x ∑ y
b=β =
n ∑ x − (∑ x )
2 2
6( −8.0249 − ( 23 .88 * −2.99 ))
b= = 1.42
6(97 .7696 − ( 23 .88 ))
2

75. DISTRIBUCION DE WEIBULL
Nos queda la siguiente ecuación:
Y = -6.15 + 1.42x
La cual utilizamos para hallar β y
η
= 1.42
a −6.15
η=e −β
η=e −1.42
= 76

76. Tabla No1

77. DISTRIBUCION DE WEIBULL
Por ultimo determinamos la fiabilidad de las
unidades a las 15 horas, puesto a operar 1
semana después de haber sido compradas.
γ =1 semana = 7 dias X 24 horas = 168 horas
R(183) = e – (183-168/76) 1.42
= 0.9049

78. DISTRIBUCION DE WEIBULL
Finalmente procedemos a calcular el MTBF Y
desviación estándar.
MTBF
= 0,9114
η WEIBULL- C
MTBF = η 0 ,9114 = 76 x 0 ,9114 = 69 , 26 horas
σ
= 0,659 WEIBULL- S
η
σ = η 0 , 659 = 76 x 0 , 659 = 50 , 08 horas
WEIBULL- P

79. EJERCICIOS
EJERCICIO N:1
Analizar y evaluar la
fiabilidad de la Torre de
Limpieza de Malta

80. PASO No. 1
ELABORAR LA ESTADISTICA DE FALLAS DE
TODOS LOS EQUIPOS DE LA UNIDAD,
PLANTA O EN EL CASO ESPECIFICO LA
TORRE DE LIMPIEZA DE MALTA

81. PASO No. 2
APLICAR LA MATRIZ DE CRITICALIDAD PARA
SELECCIONAR LOS EQUIPOS DE MAYOR
IMACTO NEGATIVO AL NEGOCIO EN CASO
DE FALLA.

82. PO = PROBABILIDAD DE OCURRENCIA
PUNTOS PROBABILIDAD DE FALLA FRECUENCIA
DE FALLA
REMOTA O RARO : No es razonable que este modo Fallas mayores
1 de falla ocurra de 3 años.
MUY BAJA O AISLADO: Basado en diseños 1 / 10000
2 similares y teniendo numero de fallas bajo.
BAJA O ESPORADICO: Basado en diseños 1/1000
3 similares que han experimentado fallas esporádicas
CONCEBIBLE: Basado en diseños similares que han 1/100
4 causado problemas.
RECURRENTE: Hay certeza que las fallas se 1/10
5 repetirán

83. PS = PROBABILIDAD DE SEVERIDAD
PUNTOS CRITERIO DE SEVERIDAD
MENOR : No hay efecto informado
1
2 MARGINAL: Fastidiosa. No hay degradación de
sistema.
3 MODERADO: Causa insatisfacción. Alguna
degradación en el sistema.
CRITICA: Causa un alto grado de insatisfacción.
4 Perdida de la función del sistema.
CATASTROFICA: Una falla que puede causar
5 muerte(s) o daños graves a la propiedad.

84. PS = PROBABILIDAD DE DETECCION
PUNTOS PROBABILIDAD DE FALLA FRECUENCIA
DE FALLA
MUY ALTA PROBABILIDAD DE DETECCIÓN de la falla 80 % - 100%
1 hasta que esta ocurra. Casi siempre hay señales de
precaución.
ALTA PROBABILIDAD DE DETECCIÓN de la falla hasta 60 % - 80%
2 que esta ocurra. La mayoría de las veces está precedida
por una señal de precaución.
PROBABILIDAD DE DETECCIÓN MODERADA de la falla 40 % - 60%
3 hasta que esta ocurra. Cerca del 50% de oportunidad de
tener una señal de precaución
BAJA PROBABILIDAD DE DETECCIÓN de la falla hasta 20 % - 40%
4 que esta ocurra. La mayoría de las veces hay una pequeña
o ninguna señal de precaución.
REMOTA PROBABILIDAD DE DETECCIÓN de la falla 0 % - 20%
5 hasta que esta ocurra. Siempre sin ninguna señal de
precaución

85. EQUIPO 1: ELEVADOR No. 10
PO = PROBABILIDAD DE OCURRENCIA
PUNTOS PROBABILIDAD DE FALLA FRECUENCIA DE FALLA
4 CONCEBIBLE 1/194
PS = PROBABILIDA DE SEVERIDAD
PUNTOS CRITERIO DE SEVERIDAD
4 CRITICO
GRADO CRITICALIDAD = PO x PS = 4x4= 16

86. EQUIPO 1: LIMPIADORA A
PO = PROBABILIDAD DE OCURRENCIA
PUNTOS PROBABILIDAD DE FALLA FRECUENCIA DE FALLA
3 ESPORADICO 1/375
PS = PROBABILIDA DE SEVERIDAD
PUNTOS CRITERIO DE SEVERIDAD
3 MODERADO
GRADO CRITICALIDAD = PO x PS = 3x3= 9

87. MATRIZ DE RIESGO
SEVERIDAD FRECUENCIA
PU PERSONAS PROCESO MEDIO CLIENTES IMAGEN
NT AMBIENTE 1 2 3 4 5
OS
LESION NO HAY EFECTO NO HAY IMPACTO
1 LEVE LEVE EFECTO LEVE RIESGO BAJO
LESION FASTIDIO EFECTO FASTIDIO IMPACTO
2 MENOR MENOR INDIVIDUA
L
LIMITAD0 RIESGO
MEDIO
LESION INESTABIL EFECTO INSATISFA IMPACTO
3 MAYOR IDAD LOCALIZ. CION
VARIOS
MAYOR EQ2
UNA ALTA EFECTO PERDIDA IMPACTO
4 MUERTE INESTABIL
IDAD
MAYOR INDIVIDUA
L
NACIONAL EQ1
VARIAS GRAVES EFECTO PERDIDA IMPACTO
5 MUERTE DAÑOS MASIVO MASIVA INTER.
RIESGO ALTO

88. EQUIPO DE MAYOR IMPACTO
EQUIPO
SELECCIONADO
ELEVADOR No10

89. PASO No. 3
APLICAR LA DISTRIBUCION DE WEIBULL A
LA DATOS ESTADISTICOS DE FALLA DEL
ELEVADOR No 10.
WEIBULL-C REGRESION

90. Fin de la
sección