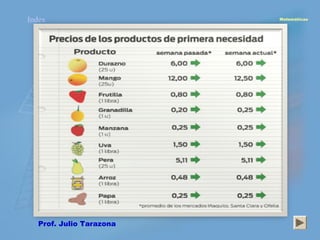
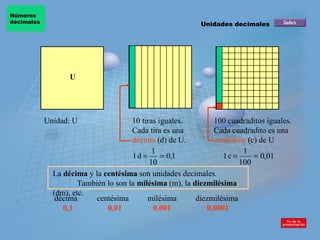
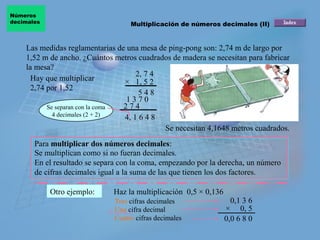
El documento presenta información sobre números decimales. Explica las unidades decimales como décimas y centésimas. Describe cómo se puede descomponer un número decimal en unidades, décimas, centésimas y otras unidades decimales. También cubre cómo sumar, restar, multiplicar y dividir números decimales, incluyendo ejemplos de cada operación.

1. Index ......................................... Matemáticas
5º
Prof Julio Tarazona

2. Index Matemáticas
Prof. Julio Tarazona

3. Index Matemáticas
Prof. Julio Tarazona

4. Index Matemáticas
Prof. Julio Tarazona

5. Index Matemáticas

6. Index Matemáticas
NÚMEROS DECIMALES
1. Unidades decimales
2. Descomposición de un número decimal
3. Suma de números decimales
4. Resta de números decimales
5. Multiplicación con números decimales
6. División con números decimales
7. Problemas con números decimales

7. Index NÚMEROS DECIMALES Matemáticas
Lee con atención:
• Parece que en 1442 d.C. el italiano PELLOS emplea por
primera vez el punto decimal, pero sólo con un significado
muy restringido.
• Francisco Vieta en su libro "Canon Mathematicus",
separaba con un espacio la cifra de las décimas, poniendo
una raya vertical entre esta y la de las unidades.
• A Juan Muller (Regiomontano), matemático alemán del
siglo XV, se le atribuye generalmente la invención de los
decimales.
• El empleo del punto decimal para separar la parte entera
de la parte decimal se lo debemos a NEPER, sin embargo, su
uso se extendió todavía un siglo después.
• El italiano Giovanni Magini (siglo XVI y XVII) empleaba la
coma para separar la parte entera de la parte decimal, uso
que se le da hasta la actualidad.
Prof. Julio Tarazona

8. Números
decimales Unidades decimales
U
Unidad: U 10 tiras iguales. 100 cuadraditos iguales.
Cada tira es una Cada cuadradito es una
décima (d) de U. centésima (c) de U
1 1
1d = = 0,1 1c = = 0,01
10 100
La décima y la centésima son unidades decimales.
También lo son la milésima (m), la diezmilésima
(dm), etc.
décima centésima milésima diezmilésima
0,1 0,01 0,001 0,0001

9. Números
decimales Descomposición de un número decimal
Un número decimal se puede descomponer de varias formas. Veamos algunas:
Número Descomposición Lectura
2,375 2 + 0,3 + 0,07 + 0,005 2 unidades, 3 décimas, 7 centésimas y 5 milésimas
2,375 2 + 0,375 2 unidades, y 375 milésimas
2,375 2 + 0,37 + 0,005 2 unidades, 37 centésimas y 5 milésimas
Otro ejemplo: Es el mismo número:
2704,7815 153,72
153,720
millares diezmilésimas
153,7200
centenas milésimas
decenas centésimas 0153,720
unidades décimas 00153,7200
Otras observaciones: a) 27 d = 2,7; b) 2 d = 0,2;
c) 37 c = 3 d + 7 c = 0,37: d)
159 c = 1,59

10. Números
decimales Suma de números decimales
Se unen las dos barras de la figura:
5,75 m 2,50 m
5,75
La longitud de la barra resultante: + 2,50
será: 8,25
575 250 825
Observa: 5,75 + 2,50 = + = = 8,25
100 100 100 En la practica, los
sumandos se colocan en
500 70 5 575
Recuerda: 5,75 = 5 + 0,7 + 0,05 = + + = columna y se siguen
100 100 100 100 los pasos:
Para sumar números decimales:
Se escribe uno debajo de otro de modo que coincidan las unidades del mismo
orden y la coma decimal.
Se suman como si fueran números naturales.
En el resultado se coloca la coma debajo de las comas de los sumandos.

11. Números
decimales Resta de números decimales
De una barra que mide 4,35 m se corta un trozo de 1,50 m.
1,50 m
4,35 m
La longitud de la barra resultante será: En la practica:
435 150 285 4,35
4,35 – 1,50 = − = = 2,85
100 100 100 – 1,50
2,85
Para restar números decimales:
Se escribe el menor debajo del mayor de modo que coincidan las unidades del
mismo orden y la coma decimal.
Se restan como si fueran números naturales.
En el resultado se coloca la coma debajo de las comas de los sumandos.
Ejemplos: a) 7,48 b) 214,396 c) 14,35 14,350
– 2,93 + 21,520 – 7,375 – 7,375
4,55 235,916 Están descolocados 6,975
y falta un 0

12. Números
decimales Multiplicación de un número decimal por otro natural (I)
Hubo un tiempo donde se operaba con euros y soles. Un euro valía
166,386 soles. ¿Cuántos soles valdrían 8 euros?
Para calcularlo hay que hacer la multiplicación 166,386 por 8:
166 386 166 386 · 8 1 331 088
166,386 · 8 = ·8 = = = 1 331,088
1000 1000 100
8 euros valdrían 1 331,088 soles. En la practica:
Para multiplicar un número decimal por un número natural:
Se multiplican los dos números como si fueran naturales. 166,386
En el resultado se separan con una coma, empezando por la derecha, x8
tantas cifras como tenga el número decimal. 1 331,088
Ejemplos: Haz las siguientes multiplicaciones: a) 12,8 · 7 b) 302,52 · 78
a) 12,8 b) 3 0 2,5 2
x 7 Una cifra decimal x 78 Dos cifras decimales
89,6 242016
211764
2 3 5 9 6, 5 6

13. Números
decimales Multiplicación de un número decimal por otro natural (II)
El espejo tiene forma cuadrada. ¿Cuántos metros
de marco se necesitan para enmarcarlo?
Hay que multiplicar 0,85 m por 4:
0, 8 5 metros 8 5 cm 0, 8 5 metros
× 4 × 4 × 4
3 4 0 cm 3, 4 0 metros
Se necesitan 3,40 m de marco.
Para multiplicar un número decimal por un número natural:
Se multiplican los dos números sin tener en cuenta la coma.
En el resultado se separan con la coma, empezando por la
derecha, tantas cifras decimales como tenga el número decimal.
Ejemplos: Efectúa las siguientes multiplicaciones:
a) 12,8 b) 3 0 2,5 2
× 7 Una cifra decimal × 7 Dos cifras decimales
89,6 2 4 2 0 186
211764
2 3 5 9 6, 5 6

14. Números
decimales Multiplicación de un número decimal por la unidad seguida de ceros
Veamos un ejemplo.
Una botella de agua mineral contiene 1,50 litros de agua. ¿Cuántos litros
contendrán 10 botellas?
Hay que multiplicar 1,50 x 10:
150 150 · 10 1500
1,50 · 10 = · 10 = = = 15,00 15 litros
100 100 100
Observa que la coma se ha desplazado un lugar a la derecha.
Para multiplicar un número decimal por 10, 100, 1000, …
se desplaza la coma hacia la derecha uno, dos, tres … lugares.
Otros ejemplos:
a) 230,36 × 1000 230360 (tres lugares)
b) 40,321 × 100 4032,1 (dos lugares)

15. Números
decimales Multiplicación de número decimales (I)
Las magnitudes de una mesa son 2,75 m de largo
por 1,25 m de ancho. Los metros cuadrados de
madera necesarios para fabricarla vienen dados
por el producto 2,75 · 1,25:
275 125 275 · 125 34 375
2,75 · 1,25 = · = = = 3,4375
100 100 100 · 100 10000
Se necesitan 3,4375 metros cuadrados.
Para multiplicar dos números decimales: En la practica:
Se multiplican como si fueran números naturales. 2, 7 5
Se separan en el resultado con una coma, empezando por la x 1,2 5
derecha, un número de cifras decimales igual a la suma de 1375
550
las cifras decimales que tiene los dos factores. 275
Otro ejemplo: Calcula 0,5 · 0,136 3,4 3 7 5
Tres cifras decimales 0,1 3 6
+ Una cifra decimal x 0,5
Cuatro cifras decimales 0,0 6 8 0

16. Números
decimales Multiplicación de números decimales (II)
Las medidas reglamentarias de una mesa de ping-pong son: 2,74 m de largo por
1,52 m de ancho. ¿Cuántos metros cuadrados de madera se necesitan para fabricar
la mesa?
2, 7 4
Hay que multiplicar × 1, 5 2
2,74 por 1,52
548
1370
Se separan con la coma 274
4 decimales (2 + 2) 4, 1 6 4 8
Se necesitan 4,1648 metros cuadrados.
Para multiplicar dos números decimales:
Se multiplican como si no fueran decimales.
En el resultado se separa con la coma, empezando por la derecha, un número
de cifras decimales igual a la suma de las que tienen los dos factores.
Otro ejemplo: Haz la multiplicación 0,5 × 0,136
Tres cifras decimales 0,1 3 6
+ Una cifra decimal × 0, 5
Cuatro cifras decimales 0,0 6 8 0

17. Números
decimales División de un número decimal por otro natural (I)
Un paquete de 3 cintas de vídeo cuesta 8,57 euros. ¿Cuánto cuesta una cinta?
Para averiguarlo hay que dividir 8,57 por 3:
857 857
8,57 : 3 = :3 = = 2,85
100 300
En la practica:
Una cinta cuesta 2,85 euros, 2 euros y 85 céntimos de euro.
Para dividir un número decimal por un número natural:
8,5 7 3
Se dividen los dos números como si fueran naturales. 25 2, 8 5
Al bajar la cifra de las décimas del dividendo, se coloca la 17
coma en el cociente. 2
Ejercicio: Haz la división 6,754 : 74
U dcm U dcm
Dividimos como si
6754 74 6, 7 5 4 7 4 Cociente: 0,091 unidades
fuesen dos números
naturales: 94 91 9 4 0, 0 9 1 91 milésimas
20 20 Resto: 20 milésimas

18. Números
decimales División de un número decimal por otro natural (II)
Para sujetar esta tabla a la pared se utilizan cuatro
clavos, separados a igual distancia cada uno del
siguiente. ¿Qué separación existe entre dos clavos
seguidos?
3, 7 5 metros 3
Hay que dividir 3,75 m entre 3:
07 1, 2 5
La separación entre dos clavos seguidos es de 1,25 m. 15
0
Para dividir un número decimal por un número natural:
Se comienza la división sin tener en cuenta la coma. Al bajar la cifra de los
Al bajar la cifra de las décimas del dividendo, se coloca la decímetros, se coloca la
coma en el cociente.
coma en el cociente.
Ejercicio: U dcm
3 8, 5 7 0 1 2 El cociente es 3,214, o sea,
Divide 38,57 entre 12, 2 5 3, 2 1 4 3 unidades y 214 milésimas
sacando tres decimales. 17 U dcm
50
2 Resto: 2 milésimas

19. Números
decimales División de un número decimal por la unidad seguida de ceros
Hagamos la división 902,32 : 100:
90 232 90 232
902,32 : 100 = :100 = = 9,0232
100 10000
Observa que la coma se ha desplazado dos lugares a la izquierda.
Para dividir un número decimal por 10, 100, 1000, … se
desplaza la coma hacia la izquierda uno, dos, tres … lugares.
Otros ejemplos:
a) 230,306 : 1000 0,230306 (tres lugares)
b) 40,321 : 10 4,0321 (un lugares)
c) 4,32 : 1000 0,00432 (tres lugares)

20. Números
decimales División de números decimales
Nos planteamos hacer la división 196,56 : 31,5.
Esa división es equivalente a 1965,6 : 315 Hemos multiplicado el dividendo
y el divisor por 10.
196,56 31,5 1 9 6 5,6 0 3 1 5 Así convertimos la división de dos
0 7 5 6 6, 2 4 números decimales en la división de
1260 un número decimal por otro natural.
0
Observa que añadiendo un 0 a la derecha de 1965,6 podemos seguir dividiendo
y obtener un decimal más en el cociente. (Si el resto no fuese 0 este proceso
podría continuarse).
Para dividir dos números decimales:
Se multiplican el dividendo y el divisor por 10 o por 100 o por …, de modo
que el divisor se transforme en un número natural.
A continuación se hace la división.
Ejemplos: 123,78 : 3,789 123 780 : 3 789 (En los dos casos hemos
0,267 : 1,005 267 : 1 005 multiplicado por 1000)
Caso de natural entre decimal: 78 : 3,02 7800 : 302

21. Números
decimales
¡GRACIAS POR SU ATENCIÓN!