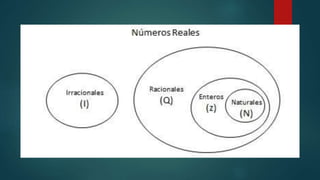
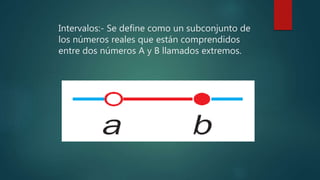
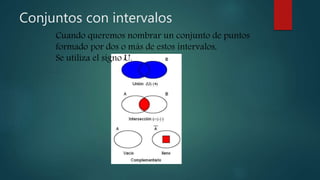
El documento habla sobre relaciones de orden y números reales. Explica que una relación binaria es de orden cuando cumple las propiedades de reflexividad, antisimetría y transitividad. También habla sobre intervalos de números reales, incluyendo intervalos cerrados, abiertos, cerrado-abiertos y operaciones entre intervalos como unión e intersección.











![Intervalos
Representar gráficamente: Representar gráficamente:
] 4 , 6 ] ( -3 , 3 [](https://image.slidesharecdn.com/numeros-reales-180608024214/85/Numeros-reales-15-320.jpg)