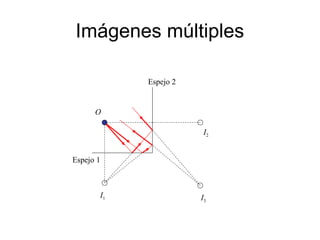
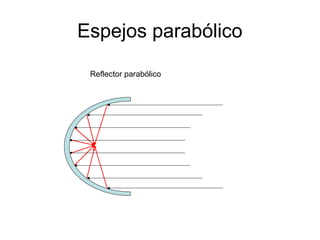
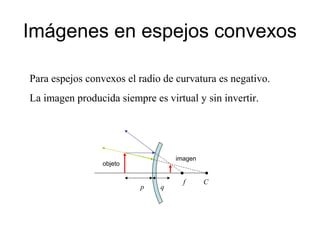
Este documento resume los principales conceptos de la óptica geométrica, incluyendo la velocidad de la luz, las leyes de reflexión y refracción, el índice de refracción, la reflexión total interna, y la formación de imágenes por espejos planos y esféricos. Explica cómo la luz se propaga en línea recta y cambia de dirección al pasar entre medios con diferentes índices de refracción. También describe cómo se forman imágenes reales e imágenes virtuales mediante espejos y lentes delg

1. Naturaleza de la luz
Física 2

2. Contenido
• Velocidad de la luz
• Óptica geométrica
• Ley de reflexión
• Ley de refracción
• Principio de Huygens
• Dispersión y prismas
• Reflexión total interna

3. Velocidad de la luz
En 1675 Ole Roemer, midió la velocidad de la luz mediante el periodo del
satélite Io de Júpiter. Valor 2.3 x 108 m/s.
En 1848 Fiseau midió la velocidad utilizando un aparato como el de la
figura
A un espejo distante
C = 2.9979 x 108 m/s

4. Naturaleza de la luz
La luz es una clase de radiación electromagnética.
Espectro electromagnético visible

5. Aproximación del rayo
La óptica geométrica estudia la propagación de la luz, con la suposición de que
la luz viaja en una dirección fija en línea recta y cambia de dirección al encintrar
una superficie diferente.
La aproximación del rayo supone que éstos son líneas perpendiculares a los
frentes de onda.
Frentes de onda
Rayos

6. Propagación de la luz
La luz se propaga en línea recta

7. Dispersión de la luz
d
l << d
l ~ d l >> d

8. Reflexión
Reflexión especular Reflexión difusa

9. Ley de reflexión
El ángulo de reflexión es igual al ángulo de incidencia.
Rayo incidente Rayo reflejado
q1
q1’
Normal

10. Ejemplo
Reflexión en espejos perpendiculares

11. Imágenes en espejos planos
Punto
luminoso
Imagen
P
C
A B
D

12. Refracción
La luz cambia de dirección al pasar de un medio a otro.

13. Ley de refracción
Normal
Rayo incidente Rayo reflejado
q1 q1’
q2
Rayo refreactado
Aire
Vidrio
v1
v2
constante
v
q
2 = 2
=
1
1
v
sen
sen
q
Donde v1 es la velocidad de la
luz en el medio 1 y v2 es la
velocidad de la luz en el
medio 2.
q1 > q2

14. q1
Vidrio v1
q2
Rayo reflejado
Normal
Aire
v2
q2 > q1

15. Índice de refracción
Definimos el índice de refracción de un medio como:
Rapidez de la luz en el vacío c
Rapidez de la luz en el medio v
n = =
A medida que la luz viaja de un medio a otro, su frecuencia no cambia pero su
longitud de onda si.
v1 = f l1 y v2 = f l2
Ya que v1 ≠ v2 se concluye que l1 ≠ l2.
2
n
1
= v = c n
1
=
2
1
2
l
1
2
/
/
n
c n
v
l
l1n1= l2n2
n1sen q1 = n2sen q2
l1
l2
n1
v1
v2
n2

16. Índices de refracción
Sustancia Índice de
refracción
Sustancia Índice de
refracción
Sólidos a 20° Líquidos a 20°C
Circona cúbica 2.20 Benceno 1.1501
Diamante (C) 2.419 Disulfuro de carbono 1.628
Fluorita (CaF2) 1.434 Tetracloruro de carbono 1.461
Vidrio de cuarso (SiO2) 1.458 Alcohol etílico 1.361
Fosfuro de galio 3.5 Glicerina 1.575
Vidrio óptico 1.52 Agua 1.333
Cristal 1.66
Hielo 1.309 Gases a 0°C 1 atm
Poliestireno 1.49 Aire 1.000293
Cloruro de sodio (NaCL) 1.544 Dioxido de carbono 1.00045

17. Ejemplo
El láser de un reproductor de discos compactos genera una luz que tiene una longitud
de onda de 780 nm en aire. A) encuentre la rapidez de esta luz una vez que entra en el
plástico de un disco compacto (n = 1.55). B) ¿cuál es la longitud de onda de esta luz
en el plástico? C) encuentre la frecuencia en el aire y en el plástico.

18. Tarea
Encuentre la dirección del rayo reflejado en el siguiente sistema de espejos
70° 135°

19. Ejemplo
Un rayo luminoso de 589 nm de l viaja a través del aire e incide en una placa de
vidrio (n = 1.52) con un ángulo de 30° con la normal, Determine el ángulo de
refracción.
30°

20. Ejemplo
q1
q2
q2
q3
d
Mostrar que q1 = q3

21. Ejemplo
El láser de un disco compacto genera una luz que tiene una
longitud de onda de 780 nm en el aire. A) encuentre la rapidez de
esta luz una vez que entra en el plástico de un disco compacto (n
= 1.55). B) ¿Cuál es la longitud de onda de la luz en el plástico?

22. Principio de Huygens
Todo punto alcanzado por un frente de ondas actúa como fuente de nuevas ondas
Frente de
onda viejo
Frente de
onda nuevo
cDt

23. Ley de Reflexión
1 2 3
A
A’
D
B C
A’ D
A C
A’C = AD
q1 q2
sen A C
AC
=
q
1
sen AD
AC
=
2
'
q
sen q1 = sen q2
q1 = q2

24. Ley de Refracción
A
A’
B
C
q2
q1
q1
q2
v1Dt
v2Dt
sen = v D
t
AC
q
sen = v D
t
2
AC
2
1
1
q
2
n
1
sen = = c n
1
=
q
2
v
1
2
q
1
2
/
/
n
c n
v
sen

25. Tarea
Un buzo ve al sol bajo el agua en un ángulo
aparente de 45º desde la vertical ¿Cuál es la
dirección real del Sol?

26. Dispersión y Prismas
d
Ángulo de desviación
Dispersión de colores

27. Reflexión total interna
Cuando un rayo va de un medio con índice de refracción mayor a otro con índice de
refracción menor se puede producir la reflexión total interna. Esta consiste en que
toda la luz es reflejada hacia la región con mayor índice de refracción.
1 2 3
sen n c q =
2
n
1
4
5
n1sen q1 = n2sen 90° = n2
Ángulo crítico

28. Ejemplo
Encuentre el ángulo crítico para la frontera agua aire (n = 1.33).

29. Fibras ópticas
Variación abrupta
Variación continua

30. ejemplo
Para luz de 389 nm calcule el ángulo crítico para los siguientes materiales rodeados de
aire: a) diamante, b) cristal y c) hielo (n = 2.42, 1.66, 1.31) . Repita para materiales
rodeados por agua (n = 1.33).

31. Tarea
Una fibra de vidrio (n = 1.5) esta sumergida en agua (1.33). ¿Cuál es el ángulo crítico
para que la luz permanezca en la fibra?

32. Principio de Fermat
Cuando un rayo de luz viaja entre dos puntos cualesquiera su
trayectoria es aquella que necesita el menor tiempo.
Como consecuencia, si el medio es homogéneo la luz se
propagará en línea recta ya que esta es la trayectoria del tiempo
mínimo.

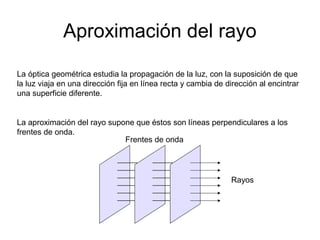
33. Ley de refracción y principio de
Fermat
P
Q
d
n1
x d – x
n2
a
b
r1
r2
q1
q2
El tiempo que toma el rayo es
( )
2 2
b d x
t = r + = + + + -
2
2 2
a x
c n
1
r
2
2
1
1
/ c / n
v
v
Derivando e igualando a cero.
( )
d a x
c
n x
1
( )
d b d x
c
( )
n d x
- -
2
2 ( )2 1/ 2
2 2 1/ 2
2 2
2
2 2
1
c[b d x ]
dt
c a x
dx
n
dx
n
dx
+ -
+
=
= + + + -
Lo cual se puede escribir como
n1sen q1 = n2sen q2

34. Tarea
Demostrar la ley de reflexión usando el principio de Fermat.

35. Espejos planos
p q
p – distancia al objeto
q – distancia a la imagen
La distancia de la imagen es
igual a la distancia del objeto
O I
espejo
Una imagen real se forma cuando los rayos pasa por y divergen
desde el punto de la imagen, una imagen virtual se forma cuando
los rayos de luz no pasan por el punto de la imagen sino que
divergen de él

36. Formación de imágenes en espejos
planos
PP p q
P’
h h’
Objeto
I
espejo
q
q
Q
R
Imagen
h’
p = q
M = 1 (no hay amplificación)
La imagen se invierta de atrás
hacia adelante no izquierda-derecha.
Aumento lateral o magnificación
Altura de la imagen
Altura de la objeto h
M = =

37. Imágenes múltiples
O
Espejo 1
I2
Espejo 2
I1 I3

38. Espejos esféricos
Centro de curvatura
R
C V
Eje principal
Espejo
O C I V

39. Aberración esférica
Aberración esférica

40. Espejos parabólico
Reflector parabólico

41. Espejos esféricos
C
V
a
p
R
q
I
O
q
h h’

42. Imágenes en espejos cóncavos
q f
objeto
f f
imagen
objeto
C C
imagen
objeto
f
C C
imagen
imagen objeto
1 + 1 = 2
p q R
1 + 1 = 1
p q f
p
R
Donde f es la distancia focal
f

43. Imágenes en espejos convexos
Para espejos convexos el radio de curvatura es negativo.
La imagen producida siempre es virtual y sin invertir.
objeto
imagen
p q
f C

44. Ejemplos de imágenes

45. Ejemplo
Suponga que cierto espejo esférico tiene una longitud focal de
+10.0 cm. Localice y describa la imagen para distancias al objeto
de a) 25.0 cm, b) 10.0 cm y c) 5.0 cm.

46. Ejemplo
La altura de una imagen real formada por un espejo cóncavo es
cuatro veces mayor que la altura del objeto cuando este se
encuentra a 30. cm frente al espejo. A) ¿Cuál es el radio de
curvatura del espejo?, b) emplee el diagrama de rayos para
localizar esta imagen.

47. ejemplo
Un espejo convexo tiene un radio de curvatura de 40 cm.
Determine la posición de la imagen virtual para distancias al objeto
de a) 30.0 cm, b) 60 cm y c) ¿las imágenes están verticales o
invertidas?

48. ejemplo
Se va a utilizar un espejo esférico para formar, sobre una pantalla
localizada a 5.0 m del objeto, una imagen cinco veces el tamaño
del objeto. A) describa el tipo de espejo requerido, b) ¿Dónde
debe colocarse el espejo en relación con el objeto.

49. ejemplo
Un rectángulo de 10.0 x 20.0 cm se coloca de manera que el
borde derecho está a 40.0 cm a la izquierda de un espejo esférico
cóncavo, como se muestra. El radio de curvatura del espejo es de
20.0 cm. A) Dibuje la imagen formada por este espejo. B) ¿cuál
es al ártea de la imagen?
40.0 cm
20.0 cm
10.0 cm C

50. Imágenes formadas por refracción
Supondremos ángulos pequeños, entonces:
Se simplifica a n1 q1 = n2 q2
Por trigonometría se cumple q1 = a + b y b = q2 + g
Para ángulos pequeños hacemos tan x = x, y sustituyendo se obtiene
n1
n1 sen q1 = n2 sen q2
n 1 2 2 1 + = -
q2
q1
n
q
p
O C
R
d
n n
R
n2
p q
I
P
a b g

51. Convención de signos
p es positiva si el objeto está enfrente de la superficie (objeto real)
p es negativa si el objeto está detrás de la superficie (objeto virtual)
q es positiva si el objeto está detrás de la superficie (imagen real)
q es negativa si el objeto está enfrente de la superficie (imagen
virtual)
R es positiva si el centro de curvatura está detrás de la superficie
convexa.
R es negativa si el centro de curvatura está enfrente de la superficie
cóncava.

52. Superficie plana
O
p
n1 n2
q
I
q n
p
n
= - 2
1

53. ejemplo
Un pez nada en el agua a una profundidad d, ¿Cuál es su
profundidad aparente?

54. Lentes delgadas
La imagen generada por la primera superficie es usada como
objeto en la segunda superficie.
Primera imagen Segunda imagen
n
n
+ = -
1 1
p1
q1
p2
Simplificando
æ
1 1 1 1 1
n + = - ( ) ÷ ÷ø
Ec. Del fabricante de lentes
q2
R1
R2
q
O
I1
1 1 1 1
I2
1 1
t
p q
n
R
p
1 1 1
R
n
2 2 2
ö
ç çè
+ = - -
R R
1 2 1 2
n
p q
ö
æ
( ) ÷ ÷ø
ç çè
= - -
R R
1 2
n
f

55. Convención de signos
p es positiva si el objeto está enfrente de la superficie (objeto real)
p es negativa si el objeto está detrás de la superficie (objeto virtual)
q es positiva si el objeto está detrás de la superficie (imagen real)
q es negativa si el objeto está enfrente de la superficie (imagen
virtual)
R1 y R2 son positiva si el centro de curvatura están detrás del lente.
R1 y R2 son negativas si el centro de curvatura están enfrente del
lente.
f es positivo si el lente es convergente.
f es negativa si el lente es divergente.

56. Lentes convergentes y divergentes

57. Lentes delgadas
1 + 1 = 1 p
p q f
M = - q

58. Lente convexa

59. Lente convexa

60. Lente cóncava

61. Microscopio simple
objeto
Imagen virtual

62. Microscopio compuesto
objeto
Imagen real aumentada
F2
F1
objetivo
ocular

63. Telescopio refractor
Rayos paralelos del objeto
distante
Imagen real
objetivo
ocular
Imagen virtual