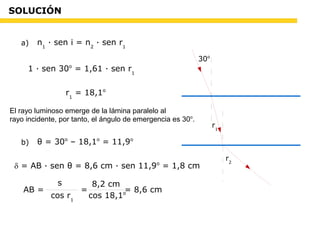
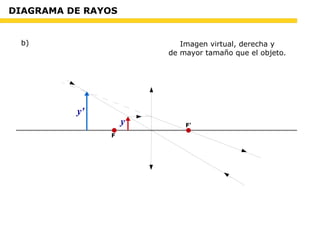
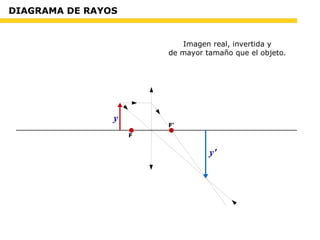
Este documento trata sobre óptica. Explica las teorías corpuscular y ondulatoria de la luz, así como conceptos como índice de refracción, reflexión, refracción y sus leyes. Incluye problemas de óptica física y geométrica sobre espejos y lentes esféricas.

1. TEMA 6.-
ÓPTICA

2. PARTE I
ÓPTICA FÍSICA

3. E = h · f c = l · f

4. NATURALEZA DE LA LUZ
TEORÍA CORPUSCULAR
Explica:
✔
Propagación rectilínea de la
luz.
✔
Formación de sombras bien
definidas.
✔
Propagación en el vacío.
✔
Fenómenos de reflexión y
refracción.
✔
Existencia de diferentes
colores.
TEORÍA ONDULATORIA
✔
Necesita de un medio material
de propagación (éter).
✔
Leyes de la reflexión, de la
refracción y las interferencias
luminosas.
✔
Propagación en línea recta y
fenómenos de difracción
quedan justificadas por la
pequeña longitud de onda de
las ondas luminosas.
✔
El color depende de la
frecuencia de las vibraciones.
✔
Fenómenos de difracción y de
polarización de la luz.

5. ÍNDICE DE REFRACCIÓN
La velocidad de la luz no es siempre la misma ya que
depende del medio transparente en que se propague.
Se denomina índice de refracción absoluto de un medio
material a la relación entre la velocidad de la luz en el
vacío c y la velocidad en dicho medio v:
Como la velocidad de la luz es menor en cualquier medio
material que en el vacío, los índices de refracción
absolutos son mayores que la unidad.
n =
c
v

6. ÍNDICE DE REFRACCIÓN
Cuando la luz se propaga en un medio material la
frecuencia no varía, se mantiene constante.
La frecuencia de una onda luminosa viene determinada
por su fuente y no es afectada por el medio.
Cuando un medio tiene mayor índice de refracción que
otro, la luz se propaga en ese medio a menor velocidad y
su longitud de onda es más pequeña.
v = l · f Si cambia la velocidad es porque
varía la longitud de onda.

7. REFLEXIÓN DE LA LUZ
Medio 1
Medio 2
Rayo
incidente Rayo
reflejado
Leyes de Snell de la reflexión:
✔
El rayo incidente, la normal y el rayo reflejado se
encuentran en el mismo plano.
✔
El ángulo de incidencia es igual al ángulo de reflexión.

8. REFRACCIÓN DE LA LUZ
Medio 1
Medio 2
Medio 1
Medio 2
n1
> n2
n1
< n2
n1
· sen i = n2
· sen r

9. REFRACCIÓN DE LA LUZ
n1
· sen l = n2
· sen 90º
ÁNGULO LÍMITE Y
REFLEXIÓN TOTAL
Para ángulos de incidencia mayores que el ángulo límite
no se produce refracción y toda la luz se refleja.
Este fenómeno, que sólo puede producirse cuando la luz
pasa de un medio más refringente a otro menos
refringente (n1
> n2
) se denomina reflexión total.

10. PROBLEMA
Una onda luminosa, que se propaga en el vacío, tiene
una frecuencia de 6,2·1014
Hz. Calcula:
a) Su periodo.
b) Su longitud de onda, ¿a qué color del espectro visible
pertenece?

11. PROBLEMA
Calcula la frecuencia y el periodo de una onda
electromagnética de 2,5 cm de longitud de onda. ¿Qué
tipo de onda es?

12. PROBLEMA
Los índices de refracción absolutos del agua y el vidrio
para la luz amarilla del sodio son 1,33 y 1,52
respectivamente. Calcula:
a) La velocidad de propagación de esta luz en el agua y
en el vidrio.
b) El índice de refracción relativo del vidrio respecto al
agua.

13. PROBLEMA
El índice de refracción absoluto del diamante es 2,38
para una luz cuya longitud de onda es 6200 Å en el
aire. Calcula:
a) La velocidad de esa luz en el diamante.
b) Su longitud de onda y su frecuencia en el interior del
diamante.

14. PROBLEMA
Un haz de luz monocromática incide desde el aire en el
agua con un ángulo de 30o
. Parte de la luz se refleja y
parte se refracta. Si el índice de refracción absoluto del
agua es 1,33, averigua los ángulos de reflexión y de
refracción.

15. PROBLEMA
Un rayo de luz monocromática, que se propaga en un
medio de índice de refracción 1,58, penetra en otro
medio, de índice de refracción 1,24, formando un
ángulo de incidencia de 15o
en la superficie de
discontinuidad entre ambos medios.
a) Determina el valor del ángulo de refracción.
b) Calcula el valor del ángulo límite para estos medios.

16. PROBLEMA
Un haz de luz monocromática incide sobre la superficie
de un vidrio (n = 1,54) con un ángulo de 30o
. ¿Cuánto
valen los ángulos de reflexión y refracción?

17. PROBLEMA
Cuando un rayo de luz pasa desde el benceno (n =
1,50) al agua (n = 1,33), ¿ a partir de qué ángulo se
produce la reflexión total?

18. PROBLEMA
Un haz de luz roja de 695 nm de longitud de onda en el
aire penetra en el agua (n = 1,33). Si el ángulo de
incidencia es de 35o
, ¿cuál es el ángulo de refracción?
¿Cuál es la longitud de onda y la frecuencia del haz de
luz en el agua?

19. PROBLEMA
Una lámina de vidrio de caras planas y paralelas,
situada en el aire, tiene un espesor de 8,2 cm y un
índice de refracción n = 1,61. Un rayo de luz
monocromática incide en la superficie superior de la
lámina con un ángulo de 30o
. Calcula:
a) El valor del ángulo de refracción en el interior de la
lámina y el ángulo de emergencia.
b) El desplazamiento lateral experimentado por el rayo
al atravesar la lámina y la distancia recorrida por el
rayo dentro de la lámina.

20. SOLUCIÓN
30o
r1
r2
a) n1
· sen i = n2
· sen r1
1 · sen 30o
= 1,61 · sen r1
r1
= 18,1o
El rayo luminoso emerge de la lámina paralelo al
rayo incidente, por tanto, el ángulo de emergencia es 30o
.
b) θ = 30o
– 18,1o
= 11,9o
d = AB · sen θ = 8,6 cm · sen 11,9o
= 1,8 cm
AB = = = 8,6 cm
s
cos r1
8,2 cm
cos 18,1o

21. PROBLEMA
Sobre la cara lateral de un prisma de vidrio situado en
el aire, de índice de refracción 1,45 y ángulo en el
vértice de 48o
, incide un rayo de luz monocromática con
un ángulo de 20o
. Calcula:
a) El ángulo de emergencia del rayo luminoso.
b) El ángulo de desviación sufrido por el rayo.
c) El ángulo de desviación mínima que corresponde a
este prisma.

22. SOLUCIÓN
a) n1
· sen i = n2
· sen r
1 · sen 20o
= 1,45 · sen r
r = 13,6o
j = r + r' ; r' = j – r = 48o
– 13,6o
= 34,4o
b) d = i + i' - j = 55o
– 48o
= 27o
i r i'r'
j = 48 o
1 · sen i' = 1,45 · sen r' ; i' = 55o ÁNGULO DE
EMERGENCIA
ÁNGULO DE
DESVIACIÓN
c) r = = = 24o
2 2
j 48o
1 · sen i = 1,45 · sen 24o
; i = 36,1o
dm
= 2 i – j = 2 · 36,1o
– 48o
= 24,2o
ÁNGULO DE DESVIACIÓN MÍNIMA

23. PARTE II
ÓPTICA GEOMÉTRICA

24. ÓPTICA GEOMÉTRICA
Se basa fundamentalmente en los siguientes hechos:
●
En los medios homogéneos e isótropos la luz se propaga en línea
recta.
●
A estas líneas rectas, que coinciden con la dirección de propagación
de la luz, las denominamos rayos.
●
Los rayos son independientes en su propagación: el cruce de dos o
más rayos no afecta a su trayectoria.
●
Se cumplen las leyes de la reflexión y de la refracción.
●
Los rayos de luz siguen trayectorias reversibles.

25. DEFINICIONES
DIOPTRIO: Conjunto formado por dos medios transparentes,
homogéneos e isótropos, con índices de refracción distintos,
separados por una superficie.
CENTRO DE CURVATURA: Centro de la superficie esférica a la
que pertenece el dioptrio esférico. El radio de la superficie
esférica es el radio de curvatura del dioptrio.
SISTEMA ÓPTICO: Conjunto de varios dioptrios.
EJE ÓPTICO O EJE PRINCIPAL: Eje común de todos los dioptrios
de un sistema óptico.

26. DEFINICIONES
VÉRTICE O CENTRO ÓPTICO: Punto de intersección del dioptrio
esférico con el eje óptico.
IMAGEN REAL: Si los rayos procedentes de un punto A
atraviesan un sistema óptico y convergen a la salida cortándose
en un punto A'. Las imágenes reales no se ven a simple vista y
pueden recogerse sobre una pantalla.
IMAGEN VIRTUAL: Si después de atravesar el sistema óptico los
rayos salen divergentes, son sus prolongaciones en sentido
contrario al de propagación de la luz que se cortan en un punto
A'. Las imágenes virtuales no existen realmente, se ven y no
pueden recogerse sobre una pantalla.

27. CONVENIO DE SIGNOS
FC
f
r
y
s

28. ESPEJOS ESFÉRICOS
+ = =
1 11 2
s' s f R
ML
= = -
y' s'
sy
AUMENTO
LATERAL
ECUACIÓN FUNDAMENTAL
DE LOS ESPEJOS ESFÉRICOS

29. CONSTRUCCIÓN DE IMÁGENES
Existen tres rayos cuyas trayectorias pueden ser trazadas
fácilmente:
●
Un rayo paralelo al eje óptico al reflejarse en el espejo pasa por el foco si el
espejo es cóncavo y para provenir del foco (pasa por él su prolongación en
sentido contrario) si el espejo es convexo.
●
Un rayo que pasa por el centro de curvatura de un espejo cóncavo, o se
dirige a él si el espejo es convexo (pasa por el centro de curvatura la
prolongación del rayo en sentido contrario a su propagación), incide sobre el
espejo perpendicularmente a su superficie y se refleja siguiendo la misma
trayectoria original.
●
Un rayo que pasa por el foco de un espejo cóncavo, o se dirige al foco de un
espejo convexo, se refleja paralelamente al eje óptico.

30. PROBLEMA
Delante de un espejo cóncavo cuyo radio de curvatura
es de 40 cm, se sitúa un objeto de 3 cm de altura,
perpendicularmente al eje óptico del espejo, a una
distancia de 60 cm. Calcula:
a) La distancia focal del espejo.
b) La posición de la imagen.
c) El tamaño de la imagen.
d) Construye gráficamente la imagen.

31. DIAGRAMA DE RAYOS
d)
y'
y
Imagen real, invertida y
de menor tamaño que el objeto.
C
F

32. PROBLEMA
Un objeto de 12 mm de altura se encuentra delante de
un espejo convexo de 20 cm de radio, a 10 cm del
vértice del mismo.
a) ¿Cómo es la imagen formada por el espejo y dónde
está situada?
b) Efectúa la construcción geométrica de la imagen.

33. DIAGRAMA DE RAYOS
b)
y'y
Imagen virtual, derecha y
de menor tamaño que el objeto.
F C

34. PROBLEMA
Un objeto situado 12 cm por delante de un espejo
cóncavo origina una imagen virtual cuatro veces mayor
que él. ¿Cuál es el radio de curvatura y la distancia focal
del espejo?

35. EJERCICIO 9 EvAU
Un objeto de 4 cm de altura se sitúa a 6 cm por delante
de la superficie cóncava de un espejo esférico. Si la
imagen obtenida tiene 10 cm de altura, es positiva y
virtual:
a) ¿Cuál es la distancia focal del espejo?
b) Realice un diagrama de rayos del sistema descrito.

36. DIAGRAMA DE RAYOS
b)
y'
y
Imagen virtual, invertida y
de mayor tamaño que el objeto.
C
F

37. EJERCICIO 14 EvAU
La imagen de un objeto reflejada por un espejo convexo
de radio de curvatura 15 cm es virtual y derecha, tiene
una altura de 1 cm y está situada a 5 cm del espejo.
a) Determine la posición y la altura del objeto.
b) Dibuje el diagrama de rayos correspondiente.

38. DIAGRAMA DE RAYOS
b)
y'
y
Imagen virtual, derecha y
de menor tamaño que el objeto.
F C

39. EJERCICIO 15 EvAU
Considere un espejo esférico cóncavo con un radio de
curvatura de 60 cm. Se coloca un objeto, de 10 cm de
altura, 40 cm delante del espejo. Determine:
a) La posición de la imagen del objeto e indique si ésta
es real o virtual.
b) La altura de la imagen e indique si ésta es derecha o
invertida.

40. DIAGRAMA DE RAYOS
a) b)
y'
y
Imagen real, invertida y
de mayor tamaño que el objeto.
C
F

41. LENTES DELGADAS
- = (n – 1) -
1 11
s' s R1
1
R2
ECUACIÓN FUNDAMENTAL DE LAS LENTES DELGADAS

42. LENTES DELGADAS
- =
1 11
s' s f '
ML
= =
y' s'
sy
AUMENTO
LATERAL
P = (dioptrías)
1
f '
POTENCIA

43. PROBLEMA
Determina la distancia focal de una lente bicóncava
delgada de índice de refracción n = 1,5 y cuyos radios
de curvatura son de 4 y 3 cm, respectivamente. Si se
sitúa un objeto de 1,2 cm de altura delante de la lente,
perpendicularmente al eje óptico, a 10 cm de la misma,
¿cuáles son las características de la imagen que se
forma?

44. DIAGRAMA DE RAYOS
y'
y
Imagen real, derecha y
de menor tamaño que el objeto.
FF'

45. PROBLEMA
Un objeto de 2,0 cm de altura se sitúa a 25 cm del
centro óptico de una lente convergente de 40 cm de
distancia focal.
a) Calcula la posición y el tamaño de la imagen.
b) Construye la imagen gráficamente.

46. DIAGRAMA DE RAYOS
b)
y'
y
Imagen virtual, derecha y
de mayor tamaño que el objeto.
F
F'

47. PROBLEMA
Un objeto de 10 mm de altura se sitúa a 20 cm del
centro óptico de una lente divergente de 30 cm de
distancia focal.
a) Calcula la posición y el tamaño de la imagen.
b) Construye la imagen gráficamente.

48. DIAGRAMA DE RAYOS
y'
y
Imagen virtual, derecha y
de menor tamaño que el objeto.
FF'

49. PROBLEMA
Un objeto de 1,2 cm de altura está situado a 20 cm de
una lente convergente de 14 cm de distancia focal.
Calcula la posición y el tamaño de la imagen. Halla
también la imagen gráficamente.

50. DIAGRAMA DE RAYOS
y'
y
Imagen real, invertida y
de mayor tamaño que el objeto.
F
F'

51. PROBLEMA
Determina la distancia focal de una lente biconvexa
delgada de índice de refracción n = 1,5 y cuyos radios
de curvatura son 5 y 4 cm, respectivamente. Si se sitúa
un objeto de 8 mm delante de la lente, a 10 cm de la
misma, ¿cuáles son las características de la imagen que
se forma?

52. DIAGRAMA DE RAYOS
y'
y
Imagen real, invertida y
de menor tamaño que el objeto.
F
F'

53. PROBLEMA
¿Qué tamaño tiene la imagen de la Luna observada
mediante una lente convergente de distancia focal igual
a 40 cm? Diámetro de la Luna = 3640 km. Distancia de
la Luna a la Tierra = 380000 km.

54. SOLUCIÓN
- =1 11
s' s f '
1 11
s' -3,8·10 8
m 0,4 m
- =
s' = 0,4000000004 m
ML
= =
y' s'
sy
y'
s'
s · y=
0,4000000004 m
3,8·10 8
m
· 3,64·10 6
= 3,8·10 -3
m = 3,8 mm=

55. PROBLEMA
Un sistema de dos lentes acopladas está formado por
una lente biconvexa, de índice de refracción 1,5, y otra
plano cóncava, de índice de refracción 1,6. Los radios
de las superficies curvas son todos de 10 cm.
Determina:
a) La potencia de cada lente y la del sistema.
b) La posición, el tamaño y las características de la
imagen formada por el sistema si el objeto tiene una
altura de 1 cm y está situado 12 cm delante del
sistema.

56. PROBLEMA
Dos lentes convergentes delgadas se colocan con una
separación de 60 cm. La primera lente tiene una
distancia focal de 10 cm y la segunda de 15 cm. Si un
objeto de 4 cm de altura se coloca a 20 cm de la
primera lente, ¿cuáles son la posición, el tamaño y las
características de la imagen final?

57. DIAGRAMA DE RAYOS
y1
'
y
Imagen real, derecha y
de menor tamaño que el objeto.
F
F'
F
F'
y2
'

58. EJERCICIO 17 EvAU
Se quiere obtener una imagen derecha y virtual, de 25
cm de altura, de un objeto de 10 cm de altura que se
sitúa a una distancia de 1 m de una lente delgada.
a) Calcule la potencia, en dioptrías, de la lente que
habría que usar así como el tipo de lente.
b) Realice el diagrama de rayos correspondiente.

59. DIAGRAMA DE RAYOS
y'
y
Imagen virtual, derecha y
de mayor tamaño que el objeto.
F
F'

60. EJERCICIO 18 EvAU
Una lente divergente forma una imagen virtual y
derecha de un objeto situado 10 cm delante de ella. Si
el aumento lateral es 0,4:
a) Efectúe el diagrama de rayos correspondiente.
b) Determine la distancia focal de la lente.

61. DIAGRAMA DE RAYOS
y'
y
Imagen virtual, derecha y
de menor tamaño que el objeto.
FF'

62. EJERCICIO 20 EvAU
Un objeto está situado a 3 cm a la izquierda de una
lente convergente de 2 cm de distancia focal.
a) Realice el diagrama de rayos correspondiente.
b) Determine la distancia de la imagen a la lente y el
aumento lateral.

63. DIAGRAMA DE RAYOS
y'
y
Imagen real, invertida y
de mayor tamaño que el objeto.
F
F'

64. EJERCICIO 21 EvAU
Un objeto está situado 1 cm a la izquierda de una lente
convergente de 2 cm de distancia focal.
a) Determine la posición de la imagen y el aumento
lateral.
b) Realice el diagrama de rayos correspondiente.

65. DIAGRAMA DE RAYOS
y'
y
Imagen virtual, derecha y
de mayor tamaño que el objeto.
F
F'

66. EJERCICIO 24 EvAU
Un sistema óptico está formado por dos lentes
convergentes delgadas de distancia focal 50 mm, cada
una, separadas una distancia de 200 mm. Un objeto de
20 mm de altura está situado a una distancia de 100
mm delante de la primera lente.
a) Realice el trazado de rayos de la imagen formada por
la primera lente, y calcule la posición y el tamaño de
dicha imagen.
b) Realice el trazado de rayos de la imagen formada por
el sistema óptico completo, y calcule la posición y el
tamaño de la imagen final.

67. DIAGRAMA DE RAYOS
y1
'
y
Imagen real, derecha y
de mismo tamaño que el objeto.
F
F'
F
F'
y2
'

68. EJERCICIO 25 EvAU
Un sistema óptico está constituido por dos lentes
situadas a 50 cm de distancia. La primera es de 10
dioptrías y la segunda de -10 dioptrías. Se sitúa un
objeto de altura 10 cm a una distancia de 15 cm, a la
izquierda de la primera lente.
a) Determine la posición y el tamaño de la imagen
producida por la primera lente y de la imagen final
formada por el sistema.
b) Realice un diagrama de rayos de la formación de la
imagen final.

69. DIAGRAMA DE RAYOS
y1
'
y
Imagen real, invertida y
de menor tamaño que el objeto.
F
F'
F'
F
y2
'