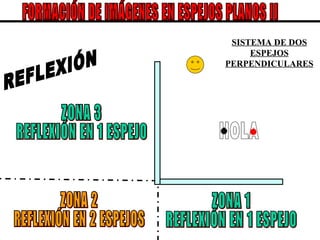
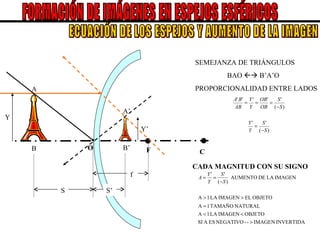
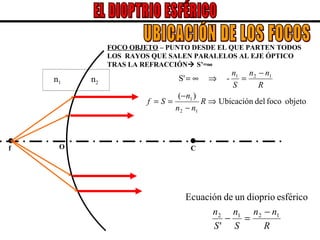
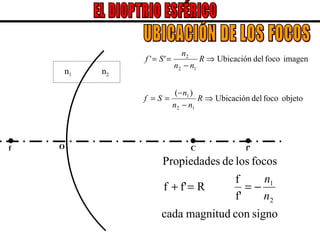
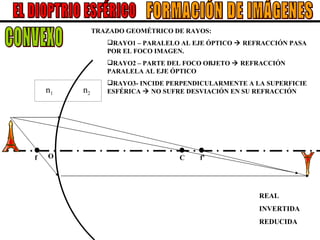
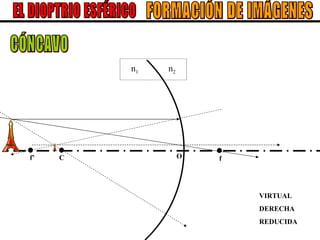
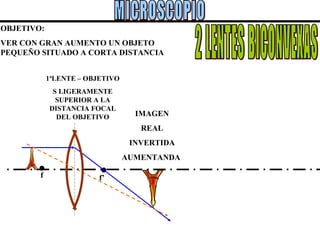
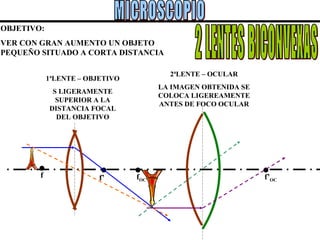
El documento describe los conceptos básicos de la formación de imágenes en óptica geométrica, incluyendo espejos planos y esféricos, así como dioptrías esféricas. Explica la terminología utilizada como centro de curvatura, radio de curvatura, foco y distancia focal. Además, describe el trazado de rayos para determinar el tipo, tamaño, posición e inversión de las imágenes formadas en cada sistema óptico.

3. ÓPTICA GEOMÉTRICA POR REFLEXIÓN

5. HOLA HOLA FORMACIÓN DE IMÁGENES EN ESPEJOS PLANOS I ESPEJO PLANO IMAGEN: VIRTUAL INVERSIÓN LATERAL MISMO TAMAÑO REFLEXIÓN

6. HOLA HOLA FORMACIÓN DE IMÁGENES EN ESPEJOS PLANOS I ESPEJO PLANO IMAGEN: VIRTUAL INVERSIÓN LATERAL MISMO TAMAÑO REFLEXIÓN PROLONGACIÓN DE LOS RAYOS – NO ES REAL

7. HOLA SISTEMA DE DOS ESPEJOS PERPENDICULARES FORMACIÓN DE IMÁGENES EN ESPEJOS PLANOS II REFLEXIÓN ZONA 1 REFLEXIÓN EN 1 ESPEJO ZONA 3 REFLEXIÓN EN 1 ESPEJO ZONA 2 REFLEXIÓN EN 2 ESPEJOS

8. HOLA HOLA SISTEMA DE DOS ESPEJOS PERPENDICULARES IMAGEN: VIRTUAL INVERSIÓN LATERAL MISMO TAMAÑO FORMACIÓN DE IMÁGENES EN ESPEJOS PLANOS II REFLEXIÓN

9. HOLA HOLA HOLA SISTEMA DE DOS ESPEJOS PERPENDICULARES IMAGEN: VIRTUAL INVERSIÓN LATERAL MISMO TAMAÑO IMAGEN: VIRTUAL SIN INVERSIÓN MISMO TAMAÑO FORMACIÓN DE IMÁGENES EN ESPEJOS PLANOS II REFLEXIÓN

10. HOLA HOLA HOLA SISTEMA DE DOS ESPEJOS PERPENDICULARES IMAGEN: VIRTUAL INVERSIÓN LATERAL MISMO TAMAÑO IMAGEN: VIRTUAL SIN INVERSIÓN MISMO TAMAÑO FORMACIÓN DE IMÁGENES EN ESPEJOS PLANOS II IMAGEN: VIRTUAL INVERSIÓN LATERAL MISMO TAMAÑO HOLA FORMACIÓN DE TRES IMÁGENES REFLEXIÓN

18. O C F O C F FORMACIÓN DE IMÁGENES EN ESPEJOS ESFÉRICOS CÓNCAVO CONVEXO FOCO – IZQUIERDA DEL ORIGEN UNIÓN DE LOS RAYOS REFLEJADOS DISTANCIA FOCAL f<0 FOCO – DERECHA DEL ORIGEN UNIÓN DE LAS PROLONGACIONES DE LOS RAY0S REFLEJADOS DISTANCIA FOCAL f>0 ESPEJOS CÓNCAVOS Y CONVEXOS:

23. FORMACIÓN DE IMÁGENES EN ESPEJOS ESFÉRICOS O C F ECUACIÓN DE LOS ESPEJOS Y AUMENTO DE LA IMAGEN NOTACIÓN Y- ALTURA DEL OBJETO Y’- ALTURA DE LA IMAGEN S – DISTANCIA DEL OBJETO AL VÉRTICE DEL ESPEJO S’ – DISTANCIA DE LA IMAGEN AL VÉRTICE DEL ESPEJO f – DISTANCIA FOCAL S S’ Y Y’ f OBJETIVO: MÉTODO MATEMÁTICO QUE NOS PERMITA CALCULAR EL TAMAÑO Y LA POSICIÓN DE LA IMAGEN FORMADA, CON LOS DATOS DEL ESPEJO.

24. FORMACIÓN DE IMÁGENES EN ESPEJOS ESFÉRICOS O C F S S’ Y Y’ A A’ B B’ SEMEJANZA DE TRIÁNGULOS BAO  B’A’O PROPORCIONALIDAD ENTRE LADOS CADA MAGNITUD CON SU SIGNO f ECUACIÓN DE LOS ESPEJOS Y AUMENTO DE LA IMAGEN

25. FORMACIÓN DE IMÁGENES EN ESPEJOS ESFÉRICOS O C F S S’ Y Y’ A A’ B B’ SEMEJANZA DE TRIÁNGULOS NMF  B’A’F APROXIAMCIÓN DE RAYOS PRÓXIMOS AL EJE ÓPTICO(PARAXIAL) PROPORCIONALIDAD ENTRE LADOS f M N CADA MAGNITUD CON SU SIGNO ECUACIÓN DE LOS ESPEJOS Y AUMENTO DE LA IMAGEN

26. FORMACIÓN DE IMÁGENES EN ESPEJOS ESFÉRICOS O C F S S’ Y Y’ A A’ B B’ RESUMEN: f M N CADA MAGNITUD CON SU SIGNO ECUACIÓN DE LOS ESPEJOS Y AUMENTO DE LA IMAGEN IMPORTANTE: ESTAS EXPRESIONES SON VÁLIDAS PARA TODOS LOS ESPEJOS ESFÉRICOS, TANTO CÓNCAVOS COMO CONVEXOS

27. FORMACIÓN DE IMÁGENES EN ESPEJOS ESFÉRICOS DISCUSIÓN DE CASOS ESPEJOS CÓNCAVOS ESPEJOS CONVEXOS EN FUNCIÓN DE LA DISTANCIA HORIZONTAL A LA QUE SITUAMOS EL OBJETO CON RESPECTO AL VÉRTICE DEL ESPEJO

35. FORMACIÓN DE IMÁGENES EN ESPEJOS ESFÉRICOS DISCUSIÓN DE CASOS - RESUMEN ESPEJOS CÓNCAVOS ESPEJOS CONVEXOS IMÁNEGES REALES E INVERTIDAS SI S>f PUEDE AUMENTAR A REDUCIR ÚNICO ESPEJO QUE DA UNA IMAGEN DERECHA Y AUMENTADA S<f SIEMPRE DA UNA IMAGEN VIRTUAL, REDUCIDA Y DERECHA ¡¡ OJO CON LOS SIGNOS !!

36. ÓPTICA GEOMÉTRICA POR REFRACCIÓN

39. EL DIOPTRIO ESFÉRICO C O n 1 n 2 P  i  r P’ NORMAL H S S’ APROXIMACIÓN PARAXIAL 1-RAYOS CON ÁNGULO MUY PEQUEÑO CON RESPECTO AL EJE ÓPTICO 2- LA DISTANCIA ENTRE O Y LA PROYECCIÓN DE H ES DESPRECIABLE    ’ P – PUNTO OBJETO P’ – PUNTO IMAGEN, TRAS LA REFRACCIÓN ENTRE AMBOS MEDIOS R

40. EL DIOPTRIO ESFÉRICO C O n 1 n 2 P  i  r P’ NORMAL H S S’    ’ OBJETIVO: RELACIONAR S Y S' CON LAS CARACTERÍSTICAS DE AMBOS MEDIOS (N1;N2 Y R) R

41. EL DIOPTRIO ESFÉRICO C O n 1 n 2 P  i  r P’ NORMAL H S S’    ’ R

42. EL DIOPTRIO ESFÉRICO C O n 1 n 2 P  i  r P’ NORMAL H S S’    ’ R

43. EL DIOPTRIO ESFÉRICO C O n 1 n 2 P  i  r P’ NORMAL H S S’    ’ R

44. EL DIOPTRIO ESFÉRICO C O UBICACIÓN DE LOS FOCOS FOCO IMAGEN – PUNTO DONDE CONVERGEN LOS RAYOS QUE INCIDEN PARALELOS AL EJE ÓPTICO  S=  f’ n 1 n 2

45. EL DIOPTRIO ESFÉRICO C O UBICACIÓN DE LOS FOCOS FOCO OBJETO – PUNTO DESDE EL QUE PARTEN TODOS LOS RAYOS QUE SALEN PARALELOS AL EJE ÓPTICO TRAS LA REFRACCIÓN  S’=  f n 1 n 2

46. EL DIOPTRIO ESFÉRICO C O UBICACIÓN DE LOS FOCOS f f’ n 1 n 2

48. EL DIOPTRIO ESFÉRICO C O FORMACIÓN DE IMÁGENES f f’ n 1 n 2 CONVEXO S S’ AUMENTO

49. EL DIOPTRIO ESFÉRICO C O FORMACIÓN DE IMÁGENES f f’ VIRTUAL DERECHA REDUCIDA n 1 n 2 CÓNCAVO

50. EL DIOPTRIO ESFÉRICO C O CONVERGENTE f’ n 1 n 2 R>0 POSITIVO  f’ (FOCO IMAGEN) > 0 SI n 1 <n 2 INCIDENCIA DE RAYOS PARALELOS CONVEXO

51. EL DIOPTRIO ESFÉRICO C O FORMACIÓN DE IMÁGENES n 1 n 2 f’ DIVERGENTE R<0 NEGATIVO  f’ (FOCO IMAGEN) < 0 SI n 1 <n 2 CRITERIO CONVENCIONAL Y AQUE SE SUPONE QUE LA LUZ PROVIENE DEL AIRE QUE TIENE ÍNDICE DE REFRACCIÓN MÁS BAJO QUE EL OTRO MEDIO INCIDENCIA DE RAYOS PARALELOS CÓNCAVO

52. EL DIOPTRIO PLANO FORMACIÓN DE IMÁGENES P P’ S S’ n 1 n 2 >

53. EL DIOPTRIO PLANO FORMACIÓN DE IMÁGENES P P’ S S’ n 1 n 2 >

56. LENTES DELGADAS C2 C1 AIRE AIRE MEDIO n P P’ O S S’ REFRACCIÓN 1) DIÓPTRIO

57. LENTES DELGADAS C2 C1 AIRE AIRE MEDIO n P P’ O S S’ REFRACCIÓN 2) DIÓPTRIO S’’ P’’

58. LENTES DELGADAS C2 C1 AIRE AIRE MEDIO n P P’ O S S’ S’’ P’’ ECUACIÓN DE UNA LENTE SI EL MEDIO NO ES AIRE, HABRÍA QUE PONER EN LUGAR DE n EL ÍNIDICE DE REFRACCIÓN RELATIVO DEL MEDIO

59. DISTANCIAS FOCALES Y POTENCIA DE LA LENTE LENTES DELGADAS ECUACIÓN DE UNA LENTE RESUMEN

60. LENTES DELGADAS TIPOS DE LENTES BICONVEXA R 1 >0 R 2 <0 PLANOCONVEXA R 1 >0 R 2 =  BICÓNCAVA R 1 <0 R 2 >0 PLANOCÓNCAVA R 1 =  R 2 >0 EL ESPESOR DE LA LENTE ES DESPRECIABLE FRENTE A LOS RADIOS DE CURVATURA CONVERGENTES DIVERGENTES PARA UNA LENTE RODEADA DE UNA MEDIO CON MENOR ÍNDICE DE REFRACCIÓN QUE EL DE LA LENTE  EN CASO CONTRARIO LA CONVERGENCIA Y DIVERGENCIA SERÍA AL REVÉS

62. LENTES DELGADAS C2 C1 AIRE AIRE O FORMACIÓN DE IMÁGENES f f’ BICONVEXAS - CONVERGENTES ACERCO EL OBJETO IMAGEN REAL INVERTIDA VA AUMENTANDO EL TAMAÑO DESDE EL INFINITO HASTA S=f S>2f IMAGEN DISMINUIDA S=2f TAMAÑO NATURAL S<2f IMAGEN AUMENTADA

63. LENTES DELGADAS C2 C1 AIRE AIRE O FORMACIÓN DE IMÁGENES f f’ BICONVEXAS - CONVERGENTES ACERCO EL OBJETO IMAGEN VIRTUAL DERECHA AUMENTANDA EFECTO LUPA

64. LENTES DELGADAS C2 C1 AIRE AIRE O FORMACIÓN DE IMÁGENES f’ f BICÓNCAVAS - DIVERGENTES ACERCO EL OBJETO IMAGEN VIRUTAL DERECHA VA AUMENTANDO EL TAMAÑO PERO SIEMPRE MENOR QUE EL OBJETO CAMBIA LA UBICACIÓN DE LOS FOCOS f  f

66. C2 C1 AIRE AIRE O f f’ 1 LENTE BICONVEXA OBJETO A UNA DISTANCIA MENOR A LA FOCAL IMAGEN VIRTUAL DERECHA AUMENTANDA LUPA

67. O f’ f 2 LENTES BICONVEXAS IMAGEN REAL INVERTIDA AUMENTANDA MICROSCOPIO OBJETIVO: VER CON GRAN AUMENTO UN OBJETO PEQUEÑO SITUADO A CORTA DISTANCIA 1ªLENTE – OBJETIVO S LIGERAMENTE SUPERIOR A LA DISTANCIA FOCAL DEL OBJETIVO

68. f’ f 2 LENTES BICONVEXAS MICROSCOPIO OBJETIVO: VER CON GRAN AUMENTO UN OBJETO PEQUEÑO SITUADO A CORTA DISTANCIA 1ªLENTE – OBJETIVO S LIGERAMENTE SUPERIOR A LA DISTANCIA FOCAL DEL OBJETIVO 2ªLENTE – OCULAR LA IMAGEN OBTENIDA SE COLOCA LIGEREAMENTE ANTES DE FOCO OCULAR f OC f’ OC

69. O f’ f MICROSCOPIO f OC f’ OC CON RESPECTO A LA SEGUNDA LENTE IMAGEN VIRTUAL DERECHA AUMENTANDA CON RESPECTO AL OBJETO INICIAL IMAGEN VIRTUAL INVERTIDA MAYOR – DOBLE AUMENTO

70. f’ f 2 LENTES BICONVEXAS IMAGEN REAL INVERTIDA REDUCIDA TELESCOPIO OBJETIVO: PODER OBSERVAR OBJETOS MUY ALEJADOS DONDE S   1ªLENTE – OBJETIVO S   CON LO CUAL LA IMAGEN SE FORMA EN EL PLANO FOCAL DE IMAGEN

71. 2 LENTES BICONVEXAS TELESCOPIO OBJETIVO: PODER OBSERVAR OBJETOS MUY ALEJADOS DONDE S   1ªLENTE – OBJETIVO S   CON LO CUAL LA IMAGEN SE FORMA EN EL PLANO FOCAL DE IMAGEN f’=f OC f DISTANCIAS FOCALES IGUALES Focular=Fobjeto f’ OC

72. TELESCOPIO f’=f OC f f’ OC CON RESPECTO A LA SEGUNDA LENTE IMAGEN VIRTUAL DERECHA AUMENTANDA CON RESPECTO AL OBJETO INICIAL IMAGEN VIRTUAL INVERTIDA MENOR