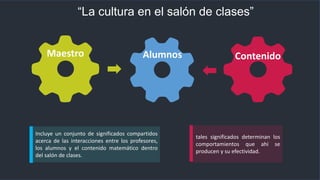
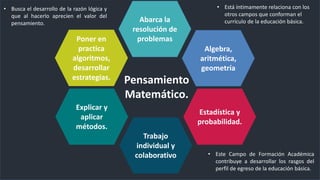
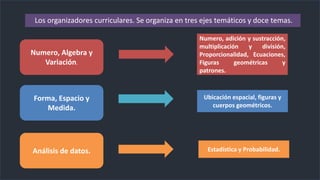
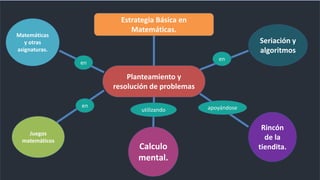
El documento aborda la enseñanza y aprendizaje del pensamiento matemático en el aula, enfatizando la importancia de la cultura en las interacciones entre profesores y estudiantes. Se destacan aspectos como la colaboración, la comunicación y la aplicación de estrategias de enseñanza que promueven el desarrollo de habilidades matemáticas a través de la resolución de problemas. Se subraya la necesidad de adaptar las estrategias de enseñanza a las características de los alumnos y su contexto para mejorar la calidad educativa.

1. CAMPO
FORMATIVO:
PENSAMIENTO MATEMATICO
1
Juan Pablo Vicente López
Karla Cristel Castro Cabrera
Margarita Muñoz Alvízar
Margarita Pérez
Universidad Pedagógica Veracruzana 603 11/04/20

2. Aprendizaje y enseñanza de las matemáticas escolares,
casos y perspectivas.
“La cultura en el salón de clases”

3. “La cultura en el salón de clases”
Incluye un conjunto de significados compartidos
acerca de las interacciones entre los profesores,
los alumnos y el contenido matemático dentro
del salón de clases.
tales significados determinan los
comportamientos que ahí se
producen y su efectividad.
Maestro Alumnos Contenido

4. La cultura esta determinada por los siguientes aspectos.
01
02
03
Favorecer unas determinadas características
de la interacción:
Dirigir la actividad hacia ideas matemáticas
centrales.
Establecimiento de normas sociometematicas.
a) Interacción de estudiantes con relación a las matemáticas
b) Tipo de actividad cognitiva que desarrolla.

5. La cultura esta determinada por los siguientes aspectos.
01
02
03
Capacidad de favorecer una interacción
especifica entre estudiantes, docente y
contenidos mediante la colaboración y discusión.
La cultura del salón se define por la manera en
que se gestiona.
Ideas como base para comprender otras
nociones matemáticas.
Rigen a la comunicación en el aula, determina lo
que pueden llegar a concebir como actividad
matemática verdadera y lo que es ilícito o no.

6. El papel del profesor en el desarrollo
de competencias.
Crear ambientes de
aprendizaje en el
aula de
matemáticas.
Lograr que los
estudiantes
reflexionen sobre
las matemáticas
que están
haciendo.
Evaluar el nivel de
comprensión de los
conceptos
matemáticos que
alcanzan sus
estudiantes.
Propiciar la
comunicación de
las ideas
matemáticas que
se producen en el
aula.

7. APRENDIZAJE
SCLAVE
“Pensamiento matemático.”
2

8. Pensamiento matemático se denomina a la
forma de razonar que utilizan los
matemáticos profesionales para resolver
problemas de diversos contextos, de la vida
diaria, ciencias o matemáticas.
Las matemáticas son un conjunto de
conceptos, métodos y técnicas mediante
los cuales es posible analizar fenómenos y
situaciones en contextos diversos;
interpretar y procesar información, tanto
cuantitativa como cualitativa; identificar
patrones y regularidades, así como
plantear y resolver problemas
Diferencian el pensamiento matemático y las matemáticas.
Pensamiento matemático Matemáticas.

9. Abarca la
resolución de
problemas
Algebra,
aritmética,
geometría
Estadística y
probabilidad.
Trabajo
individual y
colaborativo
Explicar y
aplicar
métodos.
Poner en
practica
algoritmos,
desarrollar
estrategias. Pensamiento
Matemático.
• Busca el desarrollo de la razón lógica y
que al hacerlo aprecien el valor del
pensamiento.
• Está íntimamente relaciona con los
otros campos que conforman el
currículo de la educación básica.
• Este Campo de Formación Académica
contribuye a desarrollar los rasgos del
perfil de egreso de la educación básica.

10. Utilizar de manera flexible la estimación y
calculo mental.
.
Identificar y simbolizar conjuntos de
cantidades.
Buscar, organizar, analizar e interpretar
datos con un propósito especifico. .
Propósitos generales y
específicos en relación.
Desarrollar habilidades que les permitan plantear y
resolver problemas usando herramientas
matemáticas, tomar decisiones y enfrentar
situaciones no rutinarias

11. Los organizadores curriculares. Se organiza en tres ejes temáticos y doce temas.
Numero, Algebra y
Variación.
Forma, Espacio y
Medida.
Análisis de datos.
Numero, adición y sustracción,
multiplicación y división,
Proporcionalidad, Ecuaciones,
Figuras geométricas y
patrones.
Ubicación espacial, figuras y
cuerpos geométricos.
Estadística y Probabilidad.

12. Se propone como estrategia básica que los docentes plateen situaciones problemáticas graduadas de acuerdo con el nivel
de alumnos, en el que estos pongan en juego su conocimiento matemático mediante diferentes maneras de resolverlo.
3
“Estrategias básicas de
enseñanza de las asignaturas”

13. Estrategia Básica en
Matemáticas.
Planteamiento y
resolución de problemas
Matemáticas
y otras
asignaturas.
Seriación y
algoritmos
Rincón
de la
tiendita.
Juegos
matemáticos
Calculo
mental.
en
en
utilizando
en apoyándose

14. busca que identifiquen números
que conocen mediante las
seriaciones implica discriminar y
analizar la relación que
mantienen los números.
Propósitos de las estrategias.
Implica que los alumnos
desarrollen habilidades de
conteo, medición, cálculo,
seriación, clasificación y
razonamiento
los alumnos cuentan con información y
aplicaciones reales, útiles e interesantes.
. La realización de juegos permite
interactuar, aprender y divertirse.
Mediante el planteamiento de
situaciones que generalmente
utilizan en la vida cotidiana.
Es importante se
presenten diferentes
situaciones en las que los
alumnos seleccionen,
organicen y busquen la
información

15. El pensamiento lógico matemático forma parte de nuestra
manera de comprender, entender, manipular y usar la
lógica, los números y el razonamiento para entender cómo
funciona algo, o detectar su patrón de comportamiento, a
más aún, encontrar la solución a un problema planteado
en nuestra vida cotidiana
Conclusiones.
El utilizar como apoyo los planes y programas de estudio
para guiarse en la enseñanza e implementar diferentes
estrategias, a partir de las características de los alumnos y
del contexto en el que se desarrolla, con la finalidad de
mejorar la calidad educativa que se le ofrece a nuestros
alumnos.