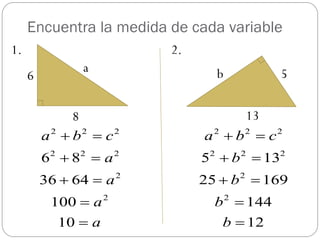
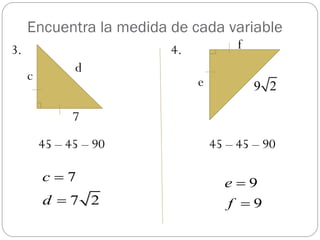
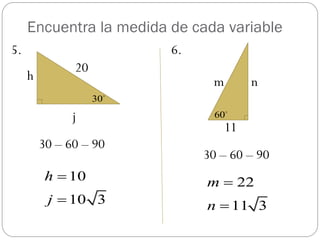
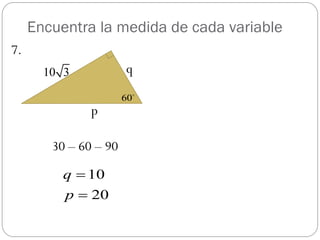
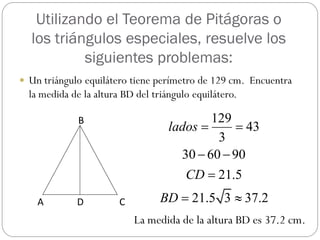
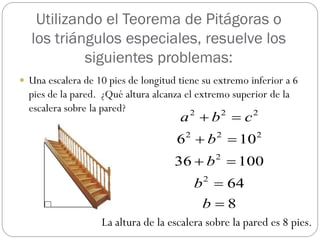
Este documento presenta el Teorema de Pitágoras y los triángulos especiales. Explica cómo usar estas herramientas matemáticas para resolver problemas que involucran medidas de triángulos rectángulos, obtusángulos y acutángulos. Luego proporciona ejemplos de problemas y sus soluciones usando estas técnicas.

1. Teorema de Pitágoras
y Triángulos Especiales
Matemática Integrada 2
Prof. Diannette Molinary Massol

2. Verifique que cada grupo de medidas
sea de un triángulo rectángulo,
obtusángulo o acutángulo.
1. 5, 7, 8 2. 10, 24, 26 3. 18, 26, 42
52  7 2  82 102  242  262 182  262  422
25  49  64 100  576  676 324  676  1764
74  64 676  676 1000  1764
acutángulo rectángulo obtusángulo

3. Encuentra la medida de cada variable
1. 2.
a b 5
6
8 13
a 2  b2  c2 a 2  b2  c2
6 8  a
2 2 2
5  b  13
2 2 2
36  64  a 2 25  b 2  169
100  a 2
b  1442
10  a b  12

4. Encuentra la medida de cada variable
3. 4. f
d
c e 9 2
7
45 – 45 – 90 45 – 45 – 90
c7 e9
d 7 2 f 9

5. Encuentra la medida de cada variable
5. 6.
20
h m n
30
j 60
11
30 – 60 – 90
30 – 60 – 90
h  10 m  22
j  10 3 n  11 3

6. Encuentra la medida de cada variable
7.
10 3 q
60
p
30 – 60 – 90
q  10
p  20

7. Utilizando el Teorema de Pitágoras o
los triángulos especiales, resuelve los
siguientes problemas:
 Un triángulo equilátero tiene perímetro de 129 cm. Encuentra
la medida de la altura BD del triángulo equilátero.
B 129
lados   43
3
30  60  90
CD  21.5
A D C BD  21.5 3  37.2
La medida de la altura BD es 37.2 cm.

8. Utilizando el Teorema de Pitágoras o
los triángulos especiales, resuelve los
siguientes problemas:
 Una escalera de 10 pies de longitud tiene su extremo inferior a 6
pies de la pared. ¿Qué altura alcanza el extremo superior de la
escalera sobre la pared?
a b  c
2 2 2
6 2  b 2  102
36  b  100
2
b 2  64
b8
La altura de la escalera sobre la pared es 8 pies.

9. Utilizando el Teorema de Pitágoras o
los triángulos especiales, resuelve los
siguientes problemas:
 La distancia entre la base de la Torre Inclinada de Pisa y su parte
más alta es de 180 pies. La torre está desviada 16 pies de su
perpendicularidad. Halla la distancia del edificio desde la parte
más alta de la torre hasta el piso.
a b  c
2 2 2
16 2  b 2  180 2
256  b 2  32400
b 2  32144
b  28 41  179.3
La distancia hasta el piso es de 179.3 pies.