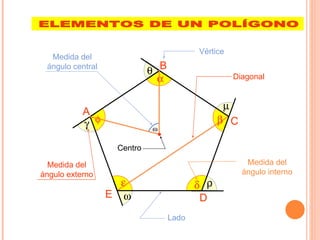
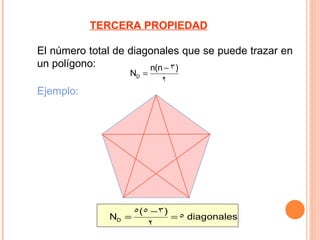
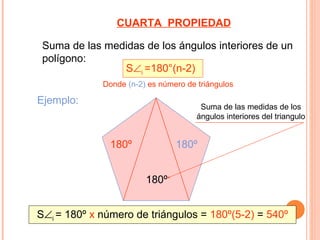
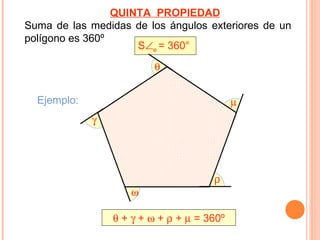
El documento describe cinco propiedades de los polígonos: 1) Los lados, vértices, ángulos interiores, exteriores y centrales son iguales. 2) Se pueden trazar (n-3) diagonales desde cada vértice, donde n es el número de lados. 3) El número total de diagonales es n(n-3)/2. 4) La suma de los ángulos interiores es 180°(n-2). 5) La suma de los ángulos exteriores es 360°.

1. Prof. William Pachas Gutierrez

2. Es la figura que esta formado por segmentos de
rectas unidos por sus extremos dos a dos.

3. Vértice
Medida del
ángulo central
θ B
α Diagonal
µ
A
γ φ ω
β C
Centro
Medida del Medida del
ángulo externo ángulo interno
ε δ ρ
E ω D
Lado

4. PRIMERA PROPIEDAD
Numéricamente: Lados, vértices, ángulos interiores,
ángulos exteriores y ángulos centrales son iguales.
• Lados
• Vértices
• Ángulos interiores
• Ángulos exteriores
• Ángulos centrales

5. SEGUNDA PROPIEDAD
A partir de un vértice de un polígono, se pueden
trazar (n-3 ) diagonales.
Ejemplo:
ND = (n-3) = (5-3) = 2 diagonales

6. TERCERA PROPIEDAD
El número total de diagonales que se puede trazar en
un polígono: n(n − 3 )
ND =
2
Ejemplo:
5(5 − 3 )
ND = = 5 diagonales
2

7. CUARTA PROPIEDAD
Suma de las medidas de los ángulos interiores de un
polígono:
S∠i =180°(n-2)
Donde (n-2) es número de triángulos
Ejemplo:
Suma de las medidas de los
ángulos interiores del triangulo
180º 180º
180º
S∠i = 180º x número de triángulos = 180º(5-2) = 540º

8. QUINTA PROPIEDAD
Suma de las medidas de los ángulos exteriores de un
polígono es 360º
S∠e = 360°
θ
Ejemplo: µ
γ
ρ
ω
θ + γ + ω + ρ + µ = 360º