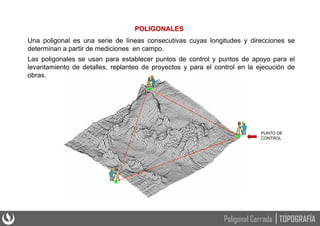
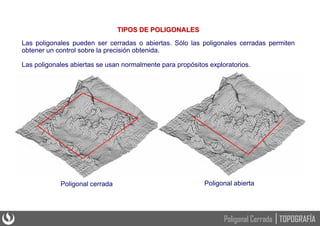
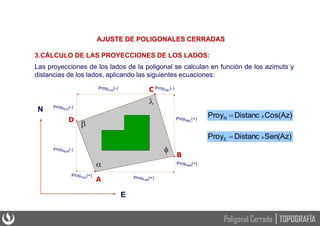
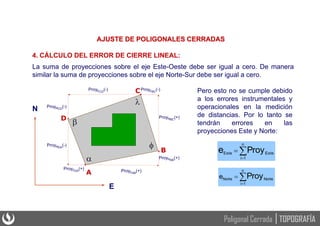
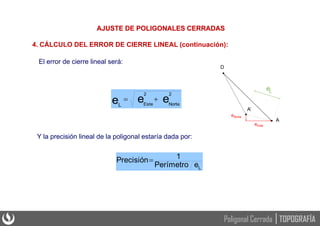
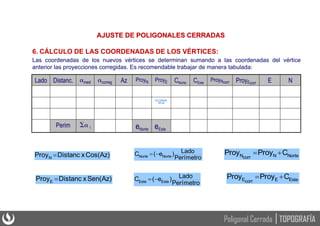
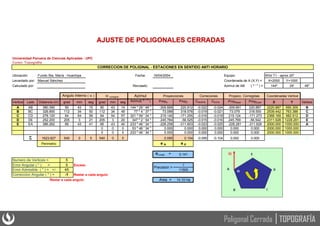
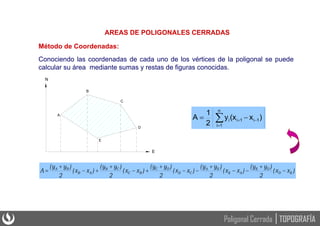
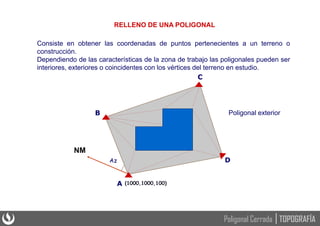
Este documento presenta los principios básicos de las poligonales cerradas en topografía, incluyendo el cálculo y ajuste de estas. Explica que una poligonal cerrada permite verificar la precisión obtenida mediante la comparación de ángulos y distancias medidas. Detalla los pasos para solucionar una poligonal cerrada, como calcular los errores de cierre angular y lineal, ajustar los ángulos y compensar el error de cierre para obtener las coordenadas rectangulares de los vértices.

1. TOPOGRAFÍA
UNIDAD 1
PRINCIPIOS BÁSICOS
PLANIMETRÍA
MEDICIONES ANGULARES
ESTACIÓN TOTAL
POLIGONAL CERRADA
COORDENADAS UTM
UNIVERSIDAD PERUANA DE CIENCIAS APLICADAS
LAUREATE INTERNATIONAL UNIVERSITIES

2. A
D
B
N
Az
(1000,1000,100)

C



POLIGONALES
• Definición
• Tipos de Poligonales
• Cálculo y Ajuste de Poligonales
Cerradas
TOPOGRAFÍA
Poligonal Cerrada

3. POLIGONALES
Una poligonal es una serie de líneas consecutivas cuyas longitudes y direcciones se
determinan a partir de mediciones en campo.
Las poligonales se usan para establecer puntos de control y puntos de apoyo para el
levantamiento de detalles, replanteo de proyectos y para el control en la ejecución de
obras.
PUNTO DE
CONTROL
TOPOGRAFÍA
Poligonal Cerrada

4. VÉRTICES DE LA POLIGONAL
Los vértices de las poligonales se materializan en campo mediante hitos de concreto.
TOPOGRAFÍA
Poligonal Cerrada

5. VÉRTICES DE LA POLIGONAL
TOPOGRAFÍA
Poligonal Cerrada

6. TIPOS DE POLIGONALES
Las poligonales pueden ser cerradas o abiertas. Sólo las poligonales cerradas permiten
obtener un control sobre la precisión obtenida.
Las poligonales abiertas se usan normalmente para propósitos exploratorios.
Poligonal cerrada Poligonal abierta
TOPOGRAFÍA
Poligonal Cerrada

7. A
D
B
N
Az
(1000,1000,100)

C



POLIGONALES CERRADAS
• Son aquellas que se inician y finalizan en el mismo vértice o en vértices diferentes
pero de coordenadas conocidas.
• Proporcionan comprobaciones de los ángulos y de las distancias medidas.
• Se emplean en levantamientos de control, levantamientos de detalles o replanteos
de obras.
Poligonal cerrada
Una poligonal cerrada queda definida por:
• Sus lados
• Sus ángulos interiores
• Las coordenadas de un vértice, que pueden
ser arbitrarias o verdaderas
• El azimut del lado de partida.
TOPOGRAFÍA
Poligonal Cerrada

8. Solucionar una poligonal consiste en el cálculo de las coordenadas rectangulares de
cada vértice.
CÁLCULO Y AJUSTE DE POLIGONALES CERRADAS
Procedimiento:
1. Cálculo y compensación del error de cierre angular.
2. Cálculo de azimutes de los lados de la poligonal.
3. Cálculo de las proyecciones de los lados.
4. Cálculo del error de cierre lineal.
5. Compensación del error lineal.
6. Cálculo de las coordenadas de los vértices.
TOPOGRAFÍA
Poligonal Cerrada

9. AJUSTE DE POLIGONALES CERRADAS
1. ERROR DE CIERRE ANGULAR:
Una vez establecidos los vértices de la poligonal se procede a medir sus ángulos
internos y las distancias de cada lado.
Debido a errores instrumentales y operacionales no siempre la suma de los ángulos
medidos coincide con la suma geométrica.
El error angular (e) esta dado por la diferencia entre el valor medido en campo y el
valor teórico.
i : ángulo interno poligonal
n : número de vértices o lados de la poligonal





n
1
i
i
α 2)
(n
180º
α
e
TOPOGRAFÍA
Poligonal Cerrada

10. 1.ERROR DE CIERRE ANGULAR (continuación):
Se debe verificar que el error angular sea menor que la tolerancia angular:
n
a
Tolerancia
a: aproximación del equipo
n : número de vértices o lados
AJUSTE DE POLIGONALES CERRADAS
La tolerancia se determina a partir de la teoría de propagación de errores:
f= i=a+b+….+n
TOPOGRAFÍA
Poligonal Cerrada

11. Si e es mayor que la tolerancia se procede a medir nuevamente los ángulos de la
poligonal.
Si e es menor que la tolerancia se procede al ajuste angular; repartiendo el error
entre todos los ángulos, asumiendo que el error es independiente de la magnitud del
ángulo medido.
n
e
C α
α 
AJUSTE DE POLIGONALES CERRADAS
C : corrección angular
e : error angular
n: número de vértices
Por ejemplo, si el equipo utilizado en la medición angular tiene una precisión de 20”,
se asume que el error repartido en cada vértice es 20”. Por tanto el error admisible
(tolerancia) se considera igual a:
TOPOGRAFÍA
Poligonal Cerrada

12. AJUSTE DE POLIGONALES CERRADAS
2. CÁLCULO DE AZIMUTES:
Los azimutes de los de lados una poligonal se pueden calcular a partir de un azimut
conocido y de los ángulos medidos.
180
180

















AB
BC
B
AB
BC
BC
luego
siendo
:
será
BC
de
azimut
El
B
AB
N
B
C
A
AB
BC

B
Datos:
Azimut AB = AB
Angulo en B = 
Azimut BC = BC = ?
TOPOGRAFÍA
Poligonal Cerrada

13. AJUSTE DE POLIGONALES CERRADAS
2. CÁLCULO DE AZIMUTES (continuación):
Generalizando el cálculo de azimut, tenemos la siguiente ecuación aplicable a
poligonales etiquetadas en sentido anti-horario.
ϕi = ϕi−1 + i ± 180º
ϕi = azimut del lado
ϕi-1 = acimut anterior
i = ángulo interno en el vértice
Aplicando los siguientes criterios:
Si (ϕi−1 + i ) < 180º se suma 180º
Si (ϕi−1 + i ) ≥ 180º se resta 180º
Si (ϕi−1 + i ) ≥ 540º se resta 540º (los azimuts son menores a 360º)
TOPOGRAFÍA
Poligonal Cerrada

14. 3.CÁLCULO DE LAS PROYECCIONES DE LOS LADOS:
Las proyecciones de los lados de la poligonal se calculan en función de los azimuts y
distancias de los lados, aplicando las siguientes ecuaciones:
AJUSTE DE POLIGONALES CERRADAS
Cos(Az)
Distanc
Proy x
N 
Sen(Az)
Distanc
Proy x
E 
N
E
A
B
D

C



ProyNAB
(+)
ProyNBC
(+)
ProyEBC
(-)
ProyECD
(-)
ProyNCD
(-)
ProyNDA
(-)
ProyEDA
(+)
ProyEAB
(+)
TOPOGRAFÍA
Poligonal Cerrada

15. La suma de proyecciones sobre el eje Este-Oeste debe ser igual a cero. De manera
similar la suma de proyecciones sobre el eje Norte-Sur debe ser igual a cero.
Pero esto no se cumple debido
a los errores instrumentales y
operacionales en la medición
de distancias. Por lo tanto se
tendrán errores en las
proyecciones Este y Norte:



n
1
i
Este
Este Proy
e



n
1
i
Norte
Norte Proy
e
AJUSTE DE POLIGONALES CERRADAS
4. CÁLCULO DEL ERROR DE CIERRE LINEAL:
N
E
A
B
D

C



ProyNAB
(+)
ProyNBC
(+)
ProyEBC
(-)
ProyECD
(-)
ProyNCD
(-)
ProyNDA
(-)
ProyEDA
(+) ProyEAB
(+)
TOPOGRAFÍA
Poligonal Cerrada

16. El error de cierre lineal será:
e
e
e
2
Norte
2
Este
L


Y la precisión lineal de la poligonal estaría dada por:
L
e
Perímetro
1
Precisión
AJUSTE DE POLIGONALES CERRADAS
4. CÁLCULO DEL ERROR DE CIERRE LINEAL (continuación):
D
A
A’
eEste
eNorte
TOPOGRAFÍA
Poligonal Cerrada

17. Determinado el error lineal se verifica que éste sea menor a la tolerancia lineal
especificada por las normas, condiciones topográficas y precisión de los equipos.
AJUSTE DE POLIGONALES CERRADAS
5. COMPENSACIÓN DEL ERROR DE CIERRE LINEAL:
El método de compensación depende de la precisión lograda por los instrumentos y
procedimientos empleados en la medición.
Algunos de los métodos de compensación utilizados son: el método de la brújula, el
del tránsito, el de Crandall, el de los mínimos cuadrados, etc.
Actualmente los equipos han igualado la precisión obtenida en la medición de
distancias con la precisión obtenida en la medición angular, lo que hace al método de
la brújula el método más adecuado para la compensación del error lineal, no sólo por
asumir esta condición sino por la sencillez de los cálculos involucrados.
TOPOGRAFÍA
Poligonal Cerrada

18. Método de la Brújula:
Método propuesto por Nathaniel Bowditch (1800) y es el más utilizado en los trabajos
normales de topografía. El método asume que :
• Los ángulos y distancias se miden con igual precisión.
• El error ocurre en proporción directa a la distancia
• Las proyecciones se corrigen proporcionalmente a la longitud de los lados.
Perímetro
Lado
)
e
(
C Norte
Norte 

Perímetro
Lado
)
e
(
C Este
Este 

5. COMPENSACIÓN DEL ERROR DE CIERRE LINEAL (continuación):
AJUSTE DE POLIGONALES CERRADAS
TOPOGRAFÍA
Poligonal Cerrada

19. Las coordenadas de los nuevos vértices se determinan sumando a las coordenadas del vértice
anterior las proyecciones corregidas. Es recomendable trabajar de manera tabulada:
Lado Distanc. med correg Az ProyN ProyE CNorte CEste
ProyNcorr ProyEcorr E N
Corr_Poligonal_
UPC.xls
Perim  i eNorte eEste
Cos(Az)
x
Distanc
ProyN 
Sen(Az)
x
Distanc
ProyE 
Norte
N
corr
N C
Proy
Proy 

Este
E
corr
E C
Proy
Proy 

Perímetro
Lado
)
e
(
C Norte
Norte 

Perímetro
Lado
)
e
(
C Este
Este 

AJUSTE DE POLIGONALES CERRADAS
6. CÁLCULO DE LAS COORDENADAS DE LOS VÉRTICES:
TOPOGRAFÍA
Poligonal Cerrada

20. AJUSTE DE POLIGONALES CERRADAS
Universidad Peruana de Ciencias Aplicadas - UPC
Curso: Topografía
Ubicación: Fundo Sta. María - Huachipa Fecha: 19/04/2004 Equipo: Wild T1 - aprox 20"
Levantado por: Manuel Sánchez Coordenada de A (X,Y) = X=2000 Y=1000
Calculado por: Revisado: Azimut de AB ( º ' " ) = 144º 29' 48''
Proyecc. Corregidas
Vertice Lado Distancia (m) grad min seg grad min seg Azimut( º ' " ) ProyN ProyE CNORTE CESTE ProyNcorr ProyEcorr X Y Vertice
A AB 380.390 90 43 15 90 43 14 144 º 29 ' 48 '' -309.669 220.912 -0.022 -0.024 -309.691 220.887 2220.887 690.309 B
B BC 326.855 112 34 50 112 34 49 77 º 4 ' 37 '' 73.099 318.576 -0.019 -0.021 73.079 318.555 2539.442 763.388 C
C CD 278.120 64 54 58 64 54 57 321 º 59 ' 34 '' 219.140 -171.255 -0.016 -0.018 219.124 -171.273 2368.169 982.512 D
D DE 252.200 205 3 21 205 3 20 347 º 2 ' 54 '' 245.784 -56.525 -0.015 -0.016 245.769 -56.542 2311.628 1228.281 E
E EA 386.262 66 43 41 66 43 40 233 º 46 ' 34 '' -228.258 -311.603 -0.023 -0.025 -228.281 -311.628 2000.000 1000.000 A
0 0 0 53 º 46 ' 34 '' 0.000 0.000 0.000 0.000 0.000 0.000 2000.000 1000.000
0 0 0 233 º 46 ' 34 '' 0.000 0.000 0.000 0.000 0.000 0.000 2000.000 1000.000
 1623.827 540 0 5 540 0 0 0.095 0.104 -0.095 -0.104 0.000 0.000 2220.887 690.309 B
Perimetro e N e E
eLineal = 0.141
Numero de Vertices = 5
Error Angular ( " ) = 5 Exceso 1
Error Admisible ( " ) = +/- 45 11500
Correccion Angular ( " ) = -1 Restar a cada angulo
Restar a cada angulo Area = 14.10 Ha
CORRECCION DE POLIGINAL - ESTACIONES EN SENTIDO ANTI HORARIO
Correciones Coordenadas Vertice
Angulo Interno (  )
Precisión =
Proyecciones
 corregido Azimut
TOPOGRAFÍA
Poligonal Cerrada

21. TOPOGRAFÍA
Poligonal Cerrada
Método de Coordenadas:
AREAS DE POLIGONALES CERRADAS
Conociendo las coordenadas de cada uno de los vértices de la poligonal se puede
calcular su área mediante sumas y restas de figuras conocidas.
N
E
A
B
C
D
E
)
x
x
(
2
)
y
y
(
)
x
x
(
2
)
y
y
(
)
x
x
(
2
)
y
y
(
)
x
x
(
2
)
y
y
(
)
x
x
(
2
)
y
y
(
A E
D
D
E
A
E
E
A
C
D
D
C
B
C
C
B
A
B
B
A


















 

n
1
i
1
i
1
i
i )
x
(x
y
2
1
A

22. TOPOGRAFÍA
Poligonal Cerrada
Método de Coordenadas:
AREAS DE POLIGONALES CERRADAS
También puede usar la fórmula determinante de Gauss:
N
E
A
B
C
D
E
Norte
A YA
B YB
C YC
D YD
E YE
A YA
Este
XA
XB
XC
XD
XE
XA
2A =  - 
A
E
C
B
B
A y
x
......
y
x
y
x 




A
E
C
B
B
A x
y
.......
x
y
x
y 




Donde:

23. RELLENO DE UNA POLIGONAL
Consiste en obtener las coordenadas de puntos pertenecientes a un terreno o
construcción.
Dependiendo de las características de la zona de trabajo las poligonales pueden ser
interiores, exteriores o coincidentes con los vértices del terreno en estudio.
A (1000,1000,100)
D
B
NM
Az
C
Poligonal exterior
TOPOGRAFÍA
Poligonal Cerrada

24. TOPOGRAFÍA
Poligonal Cerrada
Nos permite determinar el perímetro y
área del terreno.
Se efectúa un relleno interior para
obtener las curvas de nivel.
A
B
D
NM
(1000,1000,100)

C



RELLENO DE UNA POLIGONAL
Poligonal coincidente con los vértices del terreno.