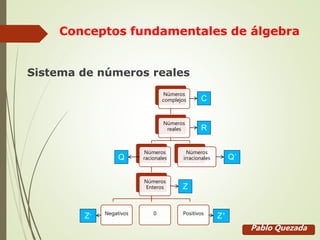
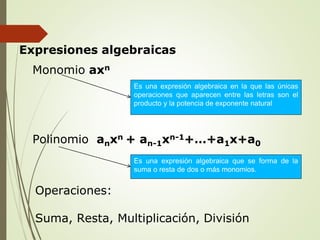
Este documento presenta conceptos fundamentales de álgebra, incluyendo los diferentes tipos de números como enteros, racionales e irracionales. Explica la notación científica, exponentes, radicales, monomios, polinomios y fórmulas para la factorización y simplificación de expresiones algebraicas.
Forma vértice de la ecuación estándar cuadrática juanreyesolvera3
Transformación de la ecuación estándar cuadrática a la forma Vértice, para identificar las coordenadas del vértice de la parábola que grafica a la ecuación.
Forma vértice de la ecuación estándar cuadrática juanreyesolvera3
Transformación de la ecuación estándar cuadrática a la forma Vértice, para identificar las coordenadas del vértice de la parábola que grafica a la ecuación.
This learner's module discusses about the topic of Radical Expressions. It also discusses the definition of Rational Exponents. It also teaches about writing an expression in a radical or exponential form. It also teaches about how to simplify expressions involving rational exponents.
Las capacidades sociomotrices son las que hacen posible que el individuo se pueda desenvolver socialmente de acuerdo a la actuación motriz propias de cada edad evolutiva del individuo; Martha Castañer las clasifica en: Interacción y comunicación, introyección, emoción y expresión, creatividad e imaginación.
ROMPECABEZAS DE ECUACIONES DE PRIMER GRADO OLIMPIADA DE PARÍS 2024. Por JAVIE...JAVIER SOLIS NOYOLA
El Mtro. JAVIER SOLIS NOYOLA crea y desarrolla el “ROMPECABEZAS DE ECUACIONES DE 1ER. GRADO OLIMPIADA DE PARÍS 2024”. Esta actividad de aprendizaje propone retos de cálculo algebraico mediante ecuaciones de 1er. grado, y viso-espacialidad, lo cual dará la oportunidad de formar un rompecabezas. La intención didáctica de esta actividad de aprendizaje es, promover los pensamientos lógicos (convergente) y creativo (divergente o lateral), mediante modelos mentales de: atención, memoria, imaginación, percepción (Geométrica y conceptual), perspicacia, inferencia, viso-espacialidad. Esta actividad de aprendizaje es de enfoques lúdico y transversal, ya que integra diversas áreas del conocimiento, entre ellas: matemático, artístico, lenguaje, historia, y las neurociencias.
ROMPECABEZAS DE ECUACIONES DE PRIMER GRADO OLIMPIADA DE PARÍS 2024. Por JAVIE...
Presentación matemáticas
1. Conceptos fundamentales de álgebra
Sistema de números reales
Números
complejos
Números
reales
Números
racionales
Números
Enteros
Negativos 0 Positivos
Números
irracionales
R
C
Q Q΄
Z
Z- Z⁺
Pablo Quezada
2. Recta de números reales
2
0 1⁄2 1-1-2 2 3
∏
R- R⁺
Notación científica
a= c x 10n , donde 1<=c<10 y n es un entero
3540000 en notación científica es 3.54 X 106
0.0000073 en notación científica es 7.3 X 10-6
Ejemplo:
3. Exponentes
Leyes
a0 = 1 (a/b)n = an /bn
a-n = 1/an
am/an = a m-n
aman = a m+n
am/an = 1/a n-m
(am)n = a mn
a-m/b-n = bn/am
(ab)n = anbn
(a/b)-n = (b/a)n
Exponentes y radicales
5. Monomio axn
Polinomio anxn + an-1xn-1+…+a1x+a0
Operaciones:
Suma, Resta, Multiplicación, División
Expresiones algebraicas
Es una expresión algebraica en la que las únicas
operaciones que aparecen entre las letras son el
producto y la potencia de exponente natural
Es una expresión algebraica que se forma de la
suma o resta de dos o más monomios.
7. (x2 y z3) (-2 x z2)(x3 y -2)
Simplificar
(-2 x3 y z5) (x3 y -2)
(-2 x6 y-1 z5)
-2 x6 z5
y
(4 a2 b)4 (- a3 / 2 b)2
(44 a2.4 b4) ( a3.2 / 22 b2)
(256 a8 b4) ( a6 / 4 b2)
256 a14b4
4b2
64 a14 b2
2.1.
(-2 x2+1 y z3+2) (x3 y -2)
a-n = 1/an
(am)n = amn
am/an = a m - n
8. Factoriza el polinomio.
45 x2 + 38 x y + 8 y2
(45 x)2 + 38 y (45 x) + 45 (8y2)
45
(45 x)2 + 38 y (45 x) + 360y2
45
(45 x + 20 y) (45 x + 18y)
45
5 (9 x + 4 y) 9 (5 x + 2y)
45
(9 x + 4 y) (5 x + 2 y)
a x2 + b x + c
