Este documento presenta conceptos básicos de matemática financiera como interés simple, interés compuesto, capital, tasa de interés y tiempo. Explica la diferencia entre interés simple e interés compuesto y cómo se calculan. También define la capitalización y cómo afecta el cálculo de intereses cuando se reinvierten periódicamente.

1. UNIVERSIDAD CENTRAL DE VENEZUELA
FACULTAD DE CIENCIAS ECONÓMICAS Y SOCIALES
ESCUELA DE ADMINISTRACIÓN Y CONTADURÍA
MATEMÁTICA FINANCIERA
Ciudad Universitaria, Mayo 2015
Blog: Mate EAC
Material elaborado
por Cariolis Roa

3. Interés
Capital
Es la cantidad de dinero cobrado o
pagado por el uso del capital durante un
tiempo.
Es el monto de dinero inicial, prestado o
depositado.

4. Tasa
Tiempo
Es la cantidad de dinero que se paga o se
cobra por cada 100 en concepto de
interés. Se expresa en porcentaje.
Se refiere al tiempo durante el cual el
dinero se encontrará prestado o
depositado y que generará intereses.

5. Es la
Acumulación
de intereses
Generados
en un lapso
de tiempo
por un
Capital Inicial
(C)
a una Tasa
de interés (i)
Obteniendo
intereses al
final de los
periodos, que
no se retiran
durante (n)
períodos de
imposición
sino que se
añaden al
capital

6. Interés Simple Interés Compuesto
Acumulación de intereses (I)
generados en un lapso de tiempo
por un Capital Inicial (C)
a una tasa de interés (i)
Durante (N) períodos de tiempo
obteniendo intereses al final de cada período
que se retiran Que NO se retiran
y se continúa calculando los
intereses sobre su Capital
Inicial.
sino que se reinvierten en el
Capital (C). Así los intereses se
calcularán a partir del Capital
Inicial más los intereses ya
generados.

7. Fórmulas
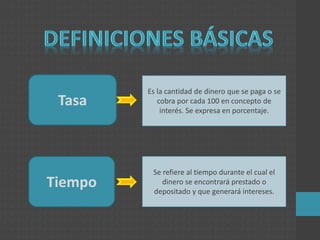
Interés Simple Interés Compuesto
I = C . i . N I = C [( 1 + i )N – 1 ]
I = Acumulación de interés
C = Capital aportado
N = Tiempo
Para comprender mejor la matemática financiera, se comparará con el
mismo ejemplo el interés simple y el interés compuesto

8. Periodo Capital
Inicial
Interés Saldo Final
0
(inicio)
100.000 (100.000 X 0,10) =
10.000
(100.000+10.000)=
110.000
1 100.000 (100.000 X 0,10) =
10.000
(110.000+10.000)=
120.000
2 100.000 (100.000 X 0,10) =
10.000
(120.000+10.000)=
130.000
3 100.000 (100.000 X 0,10) =
10.000
(130.000+10.000)=
140.000
4 100.000 (100.000 X 0,10) =
10.000
(140.000+10.000)=
150.000
5 100.000
Total 100.000 50.000 150.000
Si un Capital de 100.000 es colocado a 5 años, con una tasa de interés del 10%
anual, sucederá:
150.00010.000 x 5 = 50.000+ 100.000

9. Si un Capital de 100.000 es colocado a 5 años, con una tasa de interés del 10%
anual, sucederá:
Periodo Capital
Inicial
Interés Saldo Final
0
(inicio)
100.000 (100.000 X 0,10) =
10.000
(100.000+10.000)=
110.000
1 110.000 (110.000 X 0,10) =
11.000
(110.000 +11.000)
= 121.000
2 121.000 (121.000 X 0,10) =
12.100
(121.000 +12.100)
= 133.100
3 133.100 (133.100 X 0,10) =
13.310
(133.100 +13.310)
= 146.410
4 146.410 (146.410 X 0,10) =
14.641
(146.410 +14.641)
= 161.051
5 161.051
Total 100.000 61.051 161.051161.05161.051+ 100.000

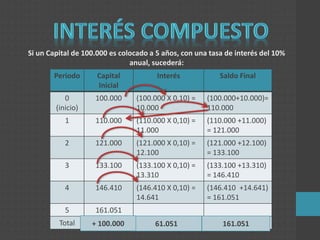
10. Interés Simple Interés Compuesto
I = C . i . N I = C [( 1 + i )N – 1 ]
I = 100.000 . 0,10 . 5 I = 100.000 [(1 + 0,10)5 - 1]
I = 50.000 I = 61.051
La diferencia está en que el interés compuesto
presenta capitalización, mientras que el simple no.
Si un Capital de 100.000 es colocado a 5 años, con una tasa de interés
del 10% anual, sucederá:
Puedes elegir hacer los ejercicios con la tabla, o bien, con las
fórmulas. Es recomendable aplicar las fórmulas para ahorrar tiempo.

11. Qué es Capitalización?

12. Así, CAPITALIZACIÓN es cuando los intereses que se
generan en cada período pasan a formar parte del
capital del siguiente período.
Es decir, esos intereses afectarán al capital y a los intereses
del siguiente período.
Primero recuerda que CAPITAL es el monto de dinero inicial,
prestado o depositado.

13. La Capitalización está determinada por el número de veces al año
que se reinvierten los intereses en el capital. Está representado por
la letra m minúscula.
Capitalización m
Anual 1
Semestral 2
Cuatrimestral 3
Trimestral 4
Capitalización m
Bimestral 6
Mensual 12
Bimensual 24
Semanal 52
Diaria 360

14. C=
𝑴
𝟏 +𝒊𝒎 𝒎
.
𝑵
M = 𝑪 𝟏 + 𝒊𝒎 𝒎 . 𝑵
N =
log 𝑀 −𝐿𝑜𝑔 𝐶
m . log 1+𝑖𝑚
I = C [( 1 + im )m . N – 1 ]
La fórmula que
aplicarás dependerá
de los datos que
conozcas.
M = C + I

15. m =
Capitalización
M = Monto
I = Acumulación
de intereses
N = períodos de
tiempo
C = Capital
Si un Capital de 100.000 es colocado
a 5 años, con una tasa de interés del
10% anual, sucederá:
M = 𝑪 𝟏 + 𝒊𝒎 𝒎 . 𝑵
im =
𝑖
𝑚
=
0,10
1
= 0,10
M = 100.000 (𝟏 + 0,10)^(1 . 5)
M = 100.000 X 1,61051
M = 161. 051m = 1
(anual)
M =?
I = ?
N = 5
C = 100.000
El monto (M) es la suma del Capital e Intereses. Así, M = C + I:
161.051 = 100.000 + I entonces: I = 61.051
i = tasa de
interés
i = 0,10

16. Puede presentarse una capitalización variable, es decir, en n periodos
aplica un número de capitalización, y en los siguientes ese número cambia.
M = 𝑪 𝟏 + 𝒊 𝒎𝟏
𝒎 𝟏 𝑵 𝟏 (𝟏 + 𝑖 𝑚2) 𝒎 𝟐(𝑵 𝟐−𝑵 𝟏)
C =
𝑴
𝟏+𝒊 𝒎𝟏
𝒎 𝟏 𝑵 𝟏 (𝟏+𝒊 𝒎𝟐 ) 𝒎 𝟐 (𝑵 𝟐 −𝑵 𝟏)

17. Si se coloca un Capital de 100.000 con una tasa de interés del 12% anual y
capitalización mensual durante los 3 primeros años; y con una tasa de interés del
18% anual y capitalización bimestral en los siguientes 2 años, cuál es el Monto?
0 1 2 3 4 5
N1 N2
m1 = 12 im1=
𝟎,𝟏𝟐
𝟏𝟐
= 0,01 m2 = 6 im2= 𝒙 =
𝟎,𝟏𝟖
𝟔
= 0,03
M = 𝑪 𝟏 + 𝟎, 𝟎𝟏 𝟏𝟐 𝑿 𝟑
(𝟏 + 𝟎, 𝟎𝟑) 𝟔 𝑿 (𝟓−𝟑)
M = 𝟏𝟎𝟎. 𝟎𝟎𝟎 𝟏 + 𝟎, 𝟎𝟏 𝟏𝟐 𝑿 𝟑
(𝟏 + 𝟎, 𝟎𝟑) 𝟔 𝑿 (𝟓−𝟑)
M = 𝟏𝟎𝟎. 𝟎𝟎𝟎 𝑿 𝟏, 𝟒𝟑𝟎𝟕𝟔𝟖𝟕𝟖𝟒 𝑿 𝟐, 𝟑𝟖𝟖𝟏𝟎𝟒𝟓𝟗𝟑
M = 341.682,54