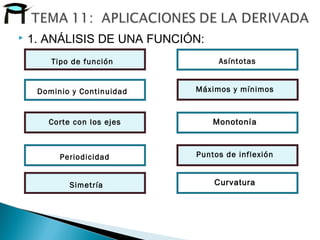
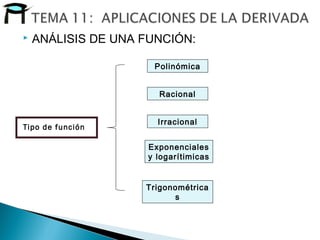
El documento trata sobre el análisis y representación de funciones. Explica cómo analizar funciones polinómicas, racionales y con condiciones, así como las aplicaciones de la derivada en problemas de optimización y en distintas áreas. También describe los métodos para determinar máximos y mínimos, monotonía, puntos de inflexión y curvatura de una función usando la derivada.

2.  1. ANÁLISIS Y REPRESENTACIÓN DE
FUNCIONES:
◦ Polinómicas
◦ Racionales.
◦ Problemas con condiciones
 2. APLICACIONES DE LA DERIVADA:
◦ En distintas áreas: Economía, Medicina, Ingeniería, Física,
etc.
◦ En problemas de optimización.

3. Corte con los ejes
Dominio y Continuidad
Tipo de función
Periodicidad
Simetría
Asíntotas
Máximos y mínimos
Monotonía
Puntos de inflexión
Curvatura
 1. ANÁLISIS DE UNA FUNCIÓN:

4.  ANÁLISIS DE UNA FUNCIÓN:
Tipo de función
Polinómica
Racional
Irracional
Exponenciales
y logarítimicas
Trigonométrica
s

5.  ANÁLISIS DE UNA FUNCIÓN:
Dominio
Conjunto de valores que toman
la variable independiente x.
Una función es continua si se
puede dibujar sin levantar el lápiz
del papel
Una función es periódica si se repite
en intervalos iguales
DominioContinuidad
Periodicidad
)()( Txfxf +=

6.  ANÁLISIS DE UNA FUNCIÓN:
Simetría
Par
Impar
)()( xfxf −=
)()( xfxf −−=
2
xy =
3
xy =

7.  ANÁLISIS DE FUNCIONES
Asíntotas
Oblicuas
Horizontales
Verticales
Polinómica
s
Racionales
NO
NO
NO SI o NO
SI o NO
SI o NO

8. Asíntota
vertical
Resolver la ecuación que se obtiene al
igualar a cero el denominador;
Se toman solo las raíces del
denominador que no lo son del
numerador
 ANÁLISIS DE FUNCIONES
◦ Racionales
Kx =
3
52
)(
−
−
=
x
x
xf Se
estudia:
)(lim xf
Kx −
→
)(lim xf
Kx +
→

9. Asíntota
vertical
Resolver la ecuación que se obtiene al
igualar a cero el denominador;
Se toman solo las raíces del
denominador que no lo son del
numerador
 ANÁLISIS DE FUNCIONES
◦ Racionales
Kx =
1
6
)( 2
−
=
x
x
xf Se
estudia:
)(lim xf
Kx −
→
)(lim xf
Kx +
→

10. Asíntota
vertical
Resolver la ecuación que se obtiene al
igualar a cero el denominador;
Se toman solo las raíces del
denominador que no lo son del
numerador
 ANÁLISIS DE FUNCIONES
◦ Racionales
Kx =
1
)( 2
+
=
x
x
xf Se
estudia:
)(lim xf
Kx −
→
)(lim xf
Kx +
→

11. Asíntota
Horizontal Se halla:Cy =
1
)( 2
+
=
x
x
xf
 ANÁLISIS DE FUNCIONES
◦ Funciones racionales
)(lim xfC
x ±∞→
=
1
6
)( 2
2
−
=
x
x
xf
1
)(
2
−
=
x
x
xf

12. Asíntota
Oblicua
1
)( 2
+
=
x
x
xf
 ANÁLISIS DE FUNCIONES
◦ Funciones racionales
1
)( 2
23
−
+
=
x
xx
xf
1
)(
2
−
=
x
x
xf
Asíntota en y=mx+b, siempre
que el grado numerador sea
una unidad mayor que el de
denominador:
y=mx+b es el
cociente
123
)( 2
24
+−
+−
=
xx
xxx
xf

13.  ANÁLISIS DE FUNCIONES
 ¿Para que se utilizan las derivadas en el análisis de
funciones?.
Máximos y mínimos relativos
Monotonía (crecimiento y
decrecimiento) de una función
Calcular los puntos de
inflexión
Curvatura (concavidad o
convexidad ) de una
función
∪
∩

14.  1. ANÁLISIS Y REPRESENTACIÓN DE
FUNCIONES:
1ª Derivada
Calcula la pendiente (m) de la recta
tangente a cualquier punto de la curva
La recta tangente algún punto de la curva
es: )( 00 xxmyy −⋅=−

15.  1. ANÁLISIS Y REPRESENTACIÓN DE
FUNCIONES:Derivada
Máximos y
mínimos
relativos
1º- Se calcula la 1ª derivada, f
´(x)
2º- Se resuelve la ecuación, f
´(x)=0
3º- Se calcula la 2ª derivada, f
´´(x)
4º- Calcular f´´(punto candidato)
Las soluciones de f´(x)=0
son los candidatos a ser
máximos o mínimos
f´´(pto. candidato)<0,
Pto. candidato es
MÁXIMO
f´´(pto. candidato)>0,
Pto candidato es
MÍNIMO5º- Calcular f(punto candidato)

16.  1. ANÁLISIS Y REPRESENTACIÓN DE
FUNCIONES:Máximos y mínimos
relativos
1º- Se calcula la 1ª derivada, f
´(x)
2º- Se resuelve la ecuación, f
´(x)=0
3º- Se calcula la 2ª derivada, f
´´(x)
4º- Calcular f´´(punto candidato)
f´´(pto. Cand.)<0,
Pto. candidato es
MÁXIMO
f´´(pto.
Cand.)>0, Pto
candidato es
MÍNIMO
5º- Calcular f(punto candidato)
Las soluciones de f´(x)=0 son los
candidatos a ser máximos o
mínimos
15)( 23
−+= xxxf

17.  1. ANÁLISIS Y REPRESENTACIÓN DE
FUNCIONES:Máximos y mínimos
relativos
1º- Se calcula la 1ª derivada, f
´(x)
2º- Se resuelve la ecuación, f´(x)=0
3º- Se calcula la 2ª derivada, f
´´(x)
4º- Calcular f´´(punto candidato)
f´´(pto. Cand.)<0,
Pto. candidato es
MÁXIMO
f´´(pto.
Cand.)>0, Pto
candidato es
MÍNIMO
5º- Calcular f(punto candidato)
Las soluciones de f´(x)=0 son los
candidatos a ser máximos o
mínimos
1
5
)(
2
−
+
=
x
x
xf

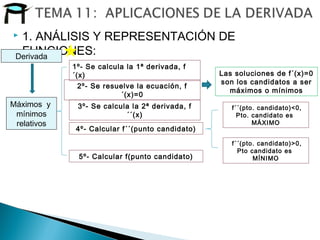
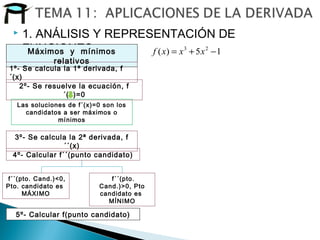
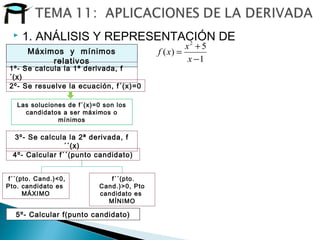
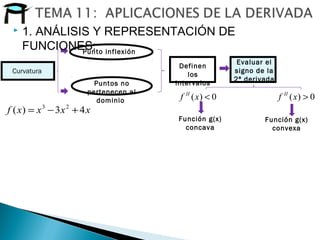
18.  1. ANÁLISIS Y REPRESENTACIÓN DE
FUNCIONES:
1
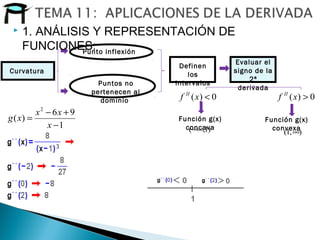
96
)(
2
−
+−
=
x
xx
xg
Monotonía
Máximos y
mínimos
Puntos no
pertenecen al
dominio
Definen
los
intervalos
Evaluar el
signo de la 1ª
derivada
0)( <xgI
0)( >xgI
Función g(x) decrece Función g(x) crece
),3[]1,( +∞∪−−∞]3,1()1,1[ ∪−
2
2
)1(
32
)(
−
−−
=
x
xx
xgI

19.  1. ANÁLISIS Y REPRESENTACIÓN DE
FUNCIONES:Puntos de inflexión
1º- Se calcula la 2ª derivada, f
´´(x)
2º- Se resuelve la ecuación, f
´´(x)=0
3º- Se calcula la 3ª derivada, f
´´´(x)
4º- Calcular f´´´(punto candidato)
f´´´(pto. Cand.) es distinto de cero.
Pto. Candidato es punto de Inflexión
Las soluciones de f´´(x)=0 son los
candidatos a ser punto inflexión
Punto donde se produce el
cambio de concavo a convexo, o
viceversa.
15)( 23
−+= xxxf

20. Puntos no
pertenecen al
dominio
Definen
los
intervalos
Evaluar el
signo de la
2ª derivada
0)( <xf II
0)( >xf II
Función g(x)
concava
Función g(x)
convexa
Punto inflexión
Curvatura
 1. ANÁLISIS Y REPRESENTACIÓN DE
FUNCIONES:
xxxxf 43)( 23
+−=

21. Puntos no
pertenecen al
dominio
Definen
los
intervalos
Evaluar el
signo de la
2ª
derivada
0)( <xf II
0)( >xf II
Función g(x)
concava
Función g(x)
convexa
Punto inflexión
Curvatura
 1. ANÁLISIS Y REPRESENTACIÓN DE
FUNCIONES:
1
96
)(
2
−
+−
=
x
xx
xg
)1,(−∞ ),1( ∞