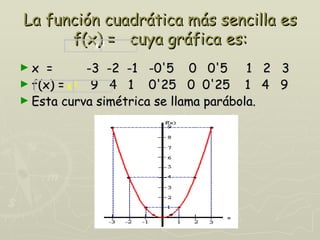
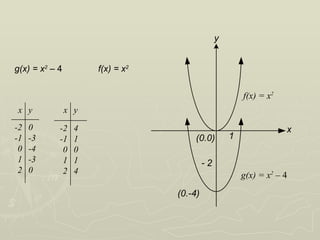
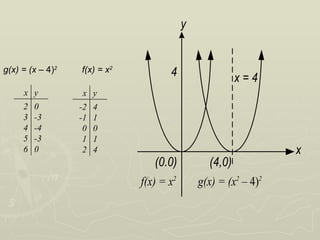
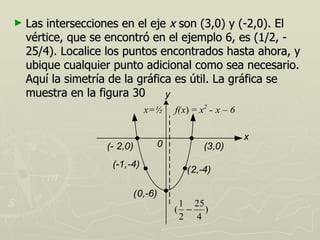
Las funciones cuadráticas son expresiones de la forma f(x) = a x² + b x + c, con a distinto de cero, y su gráfica es una parábola. El vértice de una parábola determina el punto mínimo o máximo de la función, y se puede ubicar utilizando intersecciones con los ejes. Además, se pueden comparar diferentes funciones cuadráticas para observar traslaciones y simetrías en sus gráficos.

1. FUNCIONES
CUADRATICAS

2. ► Todo número elevado al cuadrado da
como resultado un valor de signo
positivo. Es así que la ecuación
x2
y = tiene como dominio a todos los
reales y como conjunto imagen los reales
positivos incluido el cero. El valor mínimo
(en la imagen) de esta función será para
x = 0, obteniendo el punto (0, 0), al que
denominaremos vértice de la parábola.

3. ► Una función cuadrática es toda función que
pueda escribirse de la forma f(x) = a x 2+ b x
+ c, donde a, b y c son números cualesquiera,
con la condición de que a sea distinto de 0 .

4. La función cuadrática más sencilla es
f(x) = cuya gráfica es:
x 2
►x = -3 -2 -1 -0'5 0 0'5 1 2 3
► f(x) = x 2 9 4 1 0'25 0 0'25 1 4 9
► Esta curva simétrica se llama parábola.

5. ► Trace la gráfica de g(x) = x2 – 4
Al comparar las tablas de valores para g(x) = x2 -
4 y f(a) = x2 que se muestran en la figura 27,
podemos ver que para valores correspondientes de
x, los valores y de g son cada uno de 4 menos que
los de f.
Véase la figura 27. El vérti-ce de esta parábola, en
este caso el punto más bajo, está en (0, -4). El eje
de la parábola es la recta vertical x = 0.

6. y
g(x) = x2 – 4 f(x) = x2
f(x) = x2
x y x y
-2 0 -2 4 x
-1 -3 -1 1 (0.0) 1
0 -4 0 0
1 -3 1 1 -2
2 0 2 4 g(x) = x2 – 4
(0.-4)

7. ► Trace la gráfica de g(x) = (x - 4)2
Al comparar los valores que aparecen con la figura
28 se observa que la gráfica de g(x) = (x - 4)2es
la misma que la de f(x) = x2, pero trasladada 4
unidades a la derecha.
El vértice está en (4, 0). Como se muestra en la
figura 28, el eje de esta parábola es la recta
vertical x = 4.

8. y
g(x) = (x – 4)2 f(x) = x2 4 x=4
x y x y
2 0 -2 4
3 -3 -1 1
4 -4 0 0
5 -3 1 1
6 0 2 4 x
(0.0) (4,0)
f(x) = x2 g(x) = (x2 – 4)2

9. ► Trace la gráfica de la función cuadrática f(x) = x2
- x - 6.
► Como a > 0, la parábola abrirá hacia arriba. Ahora encuentre
la intersección con el eje y.
f(x) = x2 - x – 6
f(0) = 02 - x - 6 Determine f(0)
f(0) = - 6
► La intersección en el eje de y es (0, -6). Ahora encuentre las
intersecciones en el eje x.
f(x) = x2 - x – 6
0 = x2 - x – 6 sea f(x) = 0
0 = (x - 3) (x + 2) Factorice
x-3=0 o x+2=0 Igual cada factor a 0 y resuelva
x = 3 o x = -2

10. ► Las intersecciones en el eje x son (3,0) y (-2,0). El
vértice, que se encontró en el ejemplo 6, es (1/2, -
25/4). Localice los puntos encontrados hasta ahora, y
ubique cualquier punto adicional como sea necesario.
Aquí la simetría de la gráfica es útil. La gráfica se
muestra en la figura 30 y
x=½ f(x) = x2 - x – 6
x
(- 2,0) 0 (3,0)
(-1,-4)
(2,-4)
(0,-6)
1 25
( − )
2 4

11. Como hemos visto, el vértice de una parábola
vertical es el punto más alto o el punto más bajo de
la parábola. La ordenada del vértice da el valor
máximo o mínimo de y, mien-tras que la abscisa
indica en dónde ocurre ese máximo o mínimo.