1. El documento presenta un problema de probabilidad y estadística sobre subconjuntos, conjuntos y probabilidades. 2. Incluye ejercicios sobre diagramas de árbol, combinatorias, probabilidades con cartas y dados. 3. También presenta problemas para investigar sobre conjuntos y sus operaciones.

1. Dirección General de Educación Superior Tecnológica
Instituto Tecnológico de Tijuana
Departamento Académico de “Ingeniería Eléctrica y Electrónica”
Ingeniería Electrónica
Probabilidad y Estadística
5R2
Unidad 2
SALAZAR LAZARENO EDUARDO
No control: 09210873
Facilitador: MC COLUNGA ALDANA ANGELA

2. 1. Determinar cuáles de las proposiciones siguientes son verdaderas y corregir las
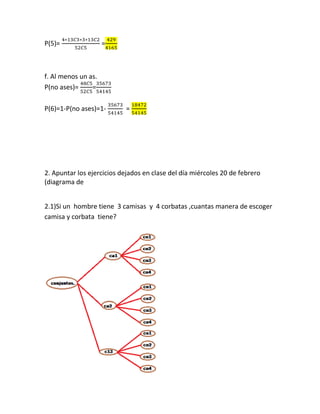
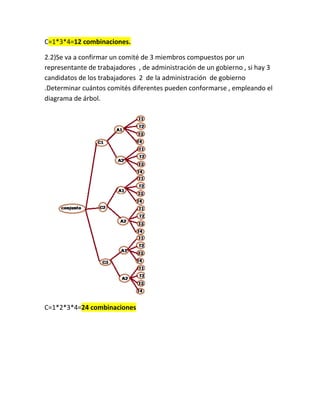
que son falsas
a.verdaro
b.Falso , Si B=(-∞,1 ] y A=(9, ∞), A no pude ser un subconjunto de B SSi :
A={X|X2=4,X<} y B={X|X≤1} , entonces B A.
Si A es un subconjunto de B , y B es un subconjunto de C , por lo tanto los subconjuntos de B se
convierten en conjuntos de C y podemos deducir que
a. {-√2}
b. {-√2, ,0,5,1/2,-4}
c. {1/2,-4}
d. {-√2, , ,0,5}
e. { ,0,}
f. {-√2, ,0,5, }
g. {1/2,-4}

3. si y solo si y .
para cualquiera x: ó
ó
Por lo tanto
inclusión:
ó
Si A={X,Y,Z} y B={R,T,Z}
= {Z}
={X,Y,Z}
= {X,Y,Z}=A
a.U={2,3,4,5,6,7,8,9,10,jack, queen, King,As,2,3,4,5,6,7,8,9,10,jack, queen, King,As,
2,3,4,5,6,7,8,9,10, jack, queen, King,As, 2,3,4,5,6,7,8,9,10, jack, queen, King,As}
b.U={2E,3E,4E,5E,6E,7E,8E,9E,10E,jackE, queenE, KingE,AsE,2D,3D,4D,5D,6D,7D,
8D,9D,10D,jackD, queenD, KingD,AsD,2T,3T,4T,5T,6T,7T,8T,9T,10T,jackT, queenT,
KingT,AsT,2C,3C,4C,5C,6C,7C,8C,9C,10C, jackC, queenC, KingC,AsC}
a. {2T,3T,4T,5T,6T,7T,8T,9T,10T,jackT,AsT, queenT, KingT , KingD, KingE, KingC}

4. b.{ KingT }
c.{KingT,KingD,KingE,KingC,2E,3E,4E,5E,6E,7E,8E,9E,10E,jackE, queenE,AsE,
2D,3D,4D,5D,6D,7D,8D,9D,10D,jackD, queenD, AsD,2C,3C,4C,5C,6C,7C,8C,9C,10C,
jackC, queenC,AsC }
d.{2E,3E,4E,5E,6E,7E,8E,9E,10E,jackE, queenE,AsE,2D,3D,4D,5D,6D,7D,8D,9D,10D
,jackD, queenD, AsD,2C,3C,4C,5C,6C,7C,8C,9C,10C, jackC, queenC,AsC }
e. { KingD,KingE,KingC }
f. {2T,3T,4T,5T,6T,7T,8T,9T,10T,jackT, queenT,AsT}
g.{2E,3E,4E,5E,6E,7E,8E,9E,10E,jackE, queenE, KingE,AsE,2D,3D,4D,5D,6D,7D,8D,
9D,10D,jackD, queenD, KingD,AsD, KingT ,2C,3C,4C,5C,6C,7C,8C,9C,10C,
jackC, queenC, KingC,AsC}
a.CAs=4/52 =1/13
b.CJackC=1/52
c.C3T o C6D= 1/52+1/52=1/26
d.CnC=13/52

5. e.CTodos –CnT =39/52
f.CnE o C10n=4/52 +12/52= 4/13
g. CnT o C4n=4/52 +12/52= 4/13
a.PRoja=6/15 =2/5
b.PBlanca=4/15
c.PAzul=5/15=1/3
d.PNo Roja=1-(6/15)=3/5
e.Pblanca o PRoja =(6/15)+(4/15) =10/15=2/3
1. Determinar la probabilidad de no obtener un total de 7 u 11 en ninguno de los
dos lanzamientos de un par de dados.
6*6=36 combinaciones posibles.
A=Combinaciones que juntos suman 7 = (1,6) (2,5) (3,4) (4,3) (5,2) (6,1) =6/36
B=Combinaciones que juntos suman 11= (5,6) (6,5)=2/36
N=A+B=6/36 + 2/36 =8/36
P=1-N=1-(8/36)=7/9
2. De una caja con 6 bolas rojas, 4 bolas blancas y 5 bolas azules se extraen tres
bolas sucesivamente. Hallar la probabilidad de que se extraigan en el orden roja,
blanca y azul si las bolas.

6. a. Se regresan (saco una bola, la tomo en cuenta y la devuelvo para sacar mi
segunda bola…).
b. No se regresan (saco una bola, me la quedo y saco mi segunda bola…).
a. Con Reemplazo
P(roja) * P(blanca) * P(azul)
6/15 * 4/15 * 5/15 = 120/3375 = 24/675
b. Sin reemplazo
P(roja) * P(blanca) * P(azul)
6/15 * 4/14 (hay una bola menos) * 5/13 (hay dos bolas menos)= 120/2730 =
127/237
3. Hallar la probabilidad de obtener al menos un 4 en dos lanzamientos de un
dado.
P( A ∪ B) = P( A)+ P( B)- P(A ∩ B)
A=4 en el primer lanzamiento.
B=4 en el Segundo lanzamiento.
P=(1/6)+( 1/6)-( (1/6)*( 1/6))=(12/36)-(1/36)=11/36
1. Se extraen 5 cartas de una baraja de 52 cartas. Hallar la probabilidad de
extraer
a. 4 ases.
P(1)= =
b. 4 ases y un rey.
P(2)= =
c. 3 ochos y 2 jotas.
P(3)= =
d. Un 9, 10, jota, reina y rey en cualquier orden.
P(4)= =
e. 3 cartas de un tipo (corazón, trébol, etc.) y 2 cartas de otro tipo.

7. P(5)= =
f. Al menos un as.
P(no ases)= =
P(6)=1-P(no ases)=1- =
2. Apuntar los ejercicios dejados en clase del día miércoles 20 de febrero
(diagrama de
2.1)Si un hombre tiene 3 camisas y 4 corbatas ,cuantas manera de escoger
camisa y corbata tiene?

8. C=1*3*4=12 combinaciones.
2.2)Se va a confirmar un comité de 3 miembros compuestos por un
representante de trabajadores , de administración de un gobierno , si hay 3
candidatos de los trabajadores 2 de la administración de gobierno
.Determinar cuántos comités diferentes pueden conformarse , empleando el
diagrama de árbol.
C=1*2*3*4=24 combinaciones

9. 2.3)De cuantas formas puede elegirse una comisión de 5 personas de entre
9 disponibles?
9C5=9!/5!(9-5)! =126
2.4) Determinar
a)AUB=1,2,4,5,7,6
b)AUC=1,2,3,4,5,7
c)A∩B=1,2
d)A∩C=1,4
e)A’UA=1,2,3,4,5,6,7,8
f)A´∩C=3,7
g)AUBUC=1,2,3,4,5,6,7
h)A∩B∩C=2,1,3,4
i)(A´∩B)U(A∩B)=1,2,3,6
j)C´∩B´=5,8
k)D∩A=1,2,4,5
D´={0}
A´∩B´∩C

10. 2.5)Una caja contiene 8 canicas rojas , 3 blancas ,9 azules , si se extraen 3
canicas aleatoriamente sin remplazamiento determinar la posibilidad que
a)Las canicas sean rojas
* * =
b)Las sean blancas
* * =
c) 2 canicas sean rojas y 1 blanca
* * =
d)Almeno 1 blanca
* * =
e)1 canica de cada color
* * =
f)Las canicas sean extraídas en este orden:roja,blanca,azul
* * =

11. Problemas a realizar o investigar.
1. ¿Es ? Justifica la solución.
Si
Por que si
A={a,b}
B={c,d}
A-B={a,b} =(A-B)’={c,d}
A’={c,d}
B’={a,b}
A’-B’={c,d}
Con eso se demuestra que la igualdad es cierta.
2. Afirmar o negar si: , entonces .
Es cierto,ya que si hacemos la resta en el siguiente es igual a conjunto vacío.
A={a,b}
B={a,b}
A-B={ }
3. Describir un espacio muestra para cada uno de los siguientes
experimentos aleatorios:
C=cara,X=cruz
a. 3 lanzamientos de una moneda.
E={(CCC),(CCX),(CXC),(XCC),(CXX),(XCX),(XXC),(XXX)}
b. El número de fumadores en un grupo de 500 hombres.
E={x|1≤x≤500}
c. Lanzar una moneda hasta que aparezca sello.
E={1,2,3,4,…..n}
d. El número de llamadas recibidas en una central telefónica.
E={x|x≥0}
e. El número de partículas nucleares que entrar a un contador Geiger.
E={x|x≥0}
f. Lanzar una moneda y un dado.
E={(C,1), (C,2), (C,3), (C,4), (C,5), (C,6), (X,1), (X,2), (X,3), (X,4), (X,5), (X,6)}
4. Apuntar los ejercicios dejados en clase el día martes 26 de febrero del
2013.

12. a)Con 7 consonantes diferentes, cuantas palabras pueden formarse que
consten de 4 consonantes 3 vocales ,no es necesario si la palabra tiene
significado.
7C4 *5C3*7P7=1764000.
b) Desarrollar los siguientes binomios.
1)(x+y)5
=x5
+5x2
y+10x3
y2
+5xy4
+y5.
2)(3+√x)3
=27+9√(x)+9x+x3/2
3)(x-1
+x2
)6
=x-6
+6x-2
x2
+15x-3
x3
+20x-4
x4
+15x-5
x5
+6x-6
x6
+x12
=x-6
+62+x12
c) Determinar la probabilidad de obtener 3 veces “6” en 5 lanzamientos de
dados.
5C3(5/6*5/6*1/6*1/6*1/6)=.032
d) Encontrar la probabilidad de que un matrimonio estén vivos dentro de 20 años
están dados por .8 para el esposo y .9 para la esposa. Hallar de .
1) Ambos vivan
P(AUB)=(.9)(.8)=.72
2) Ninguno viva
P(N v)=(1-.9)(1-.8)=.02
3)Al menos uno viva
1-P(N v)=1-.02=.98
e)Sea A={x|x2
-3x+2},B={x|x2
≤16} Determinar si A pertenece a B o no.
x2
-3x+2=0
(x-2)(x-1)=0
X1=2,X2=1
x2
≤16
x≤4
Si pertenece.
f)Sea u={1,2,3,4,5}

13. A={1,5}
B={2,5,3}
C={4,2,}
1)AU(BUC)= {U}
2)(AUB)UC={U}
3)A∩(BUC)= {5}
4)(A∩B)U(AUC)= {5}
5)A’∩(B’∩C’)= {}
6)(AUB)-(AUC)= {3}
7)(A∩C)’UB={U}
8)A-(B’∩C’)= {5}
g)Sea u el conjunto de todos los enteros no negativos
A={x|x es un entero par 1≤x<6 }
B= {x|x es un entero primo 0<x≤4}
Encontrar
1)AUB={2,3,4}
2)A∩B={2}
3)A’∩B’={x|x=1 U 5≤x<∞}
4)A-B={4}
5)(B-A)= {3}
6)(A-B)U(B-A)= {3,4}
h) Emplear el diagrama de ven para
1)A∩(BUC)

14. 2)AU(B∩C)
3)A’∩(BUC)’
4)A-(B∩C)
5)A’-(BUC)’