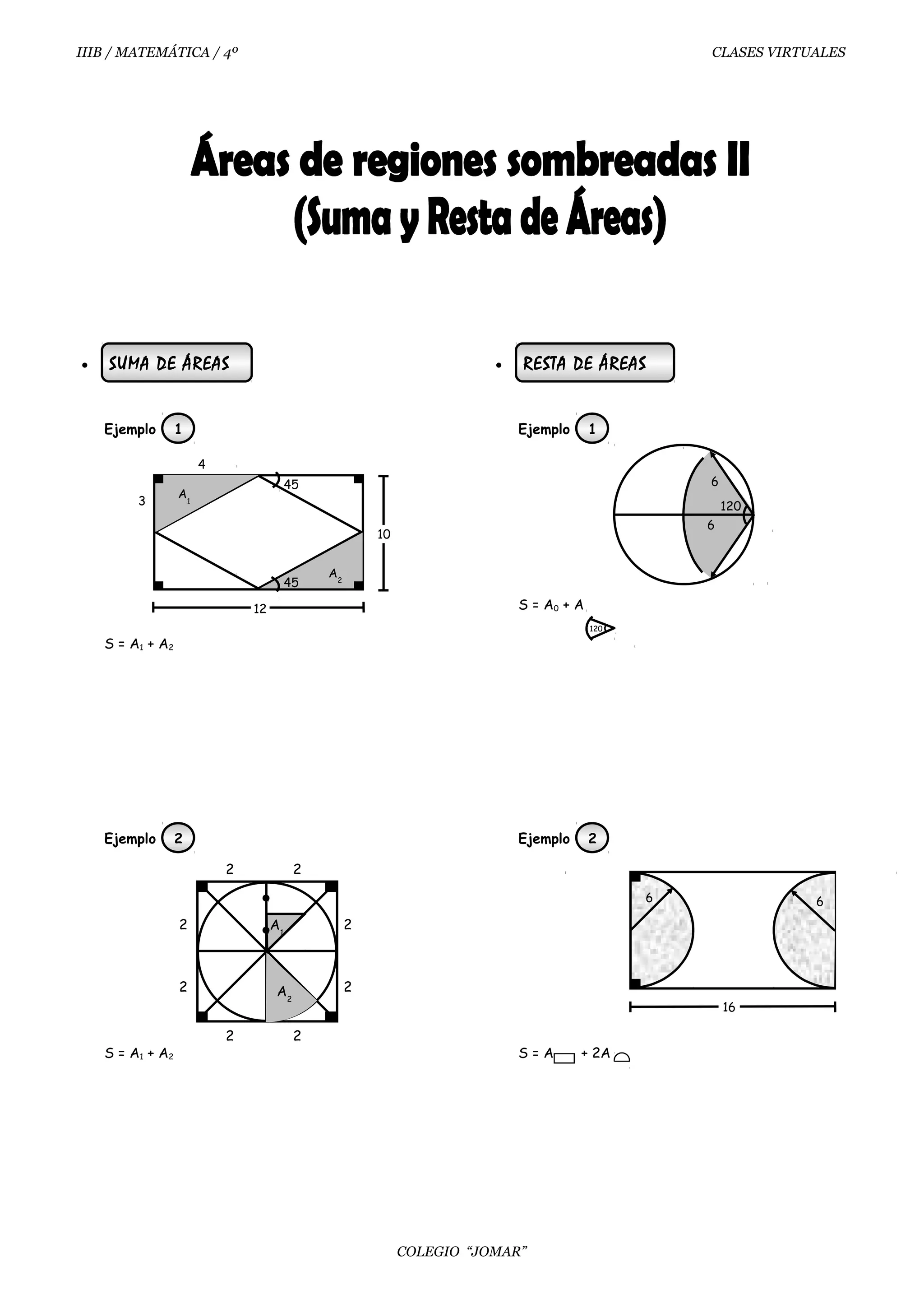
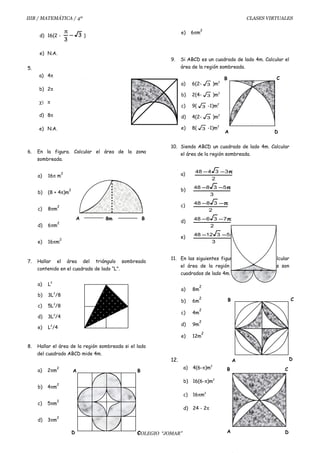
Este documento presenta una lección sobre el cálculo de áreas de figuras geométricas. Incluye ejemplos y ejercicios de suma y resta de áreas, así como problemas para calcular el área de regiones sombreadas en cuadrados, círculos y otros polígonos regulares. El estudiante debe resolver los ejercicios y mostrar los cálculos para determinar el área de cada región delimitada.

1. IIIB / MATEMÁTICA / 4º CLASES VIRTUALES
• SUMA DE ÁREAS
Ejemplo 1
S = A1 + A2
Ejemplo 2
S = A1 + A2
• RESTA DE ÁREAS
Ejemplo 1
S = A0 + A
Ejemplo 2
S = A + 2A
COLEGIO “JOMAR”
10
A1
A2
45
45
4
3
12
2 2
2 2
2 2
2 2
A2
A1
120
120
6
6
6 6
16

2. IIIB / MATEMÁTICA / 4º CLASES VIRTUALES
Las figuras que se muestran a continuación son
cuadrados de 4m de lado. Calcular Ud. el área
de la Región Sombreada.
1.
Rpta.: …………………………
2.
Rpta.: …………………………
3.
Rpta.: …………………………
4.
Rpta.: …………………………
5.
Rpta.: …………………………
6. Hallar el área de la región sombreada
(aproximadamente)
a) 4(4 - π) cm2
b) (16 - 2π) cm2
c) (8 - 2π)
d) (4 - π)
e) N.A.
7. Hallar el valor del área sombreada.
a) π + 2
b) π - 2
c) 2π + 4
d) 2π - 4
e) 6π + 8
8. Calcular el valor del área sombreada.
a) 4πD2
b) πD2
/4
c) 5πD2
/4
d) 0,75πD2
e) πD2
9. Calcular el valor del área sombreada.
a) 3 3 + 3π
b) 9 3 - π
c) 3( 3 + π)
d) 3(3 3 - π)
e) N.A.
10. Hallar el área sombreada.
a) 16(4 - π)
b) 12(2 + π)
c) 48π
d) 9π
e) 15π + 2
11. Calcular el área de la región sombreada en
función del lado “a” del hexágono regular.
COLEGIO “JOMAR”
4 cm
4 cm
2
2
D
2D
A C
B
6
6 6
8

3. IIIB / MATEMÁTICA / 4º CLASES VIRTUALES
a) )
2
3(
2
a2
π
− d) d)
)3(
4
a2
−π
b) )33(
2
a2
π− e) N.A.
c) )32(
2
a2
π−
12. Hallar el área de la región sombreada, si: “O” y
“O1” son centros, OA = OB = 4cm.
a) π cm2
b)
3
2π
c) 2π
d) 3π
e)
2
3π
13. Sea el ∆ MNP equilátero, hallar el área
sombreada.
a) 75(π + 3 3 ) d) 75(π -
4
33
)
b) 75(π - 3 3 ) e) N.A.
c) 75(π +
4
33
)
14. En un círculo de radio 1m se trazan dos
diámetros perpendiculares tomando cuatro
círculos. El área de la región sombreada es:
a) (π - 3)m
2
b) (2π - 5)m
2
c) 2πm
2
d) (2π - 7)m
2
e) (π - 2)m
2
15. Si el área del cuadrado ABCD vale 40m
2
. ¿Cuál
es el área de la figura sombreada.
a) 20m
2
b) 12m
2
c) 15m
2
d) 10m
2
e) 25m
2
TAREA DOMICILIARIA
En las figuras que se muestran a continuación
son cuadrados se 4m de lado. Calcular Ud. el
área de la Región Sombreada.
1.
a) 4(π - 2)
b) 4(π - 4)
c) 4π - 1
d) 8π - 16
e) N.A.
2.
a) 6(π + 1)
b) 6(π - 1)
c) 6(2 - π)
d) 6 - 2π
e) N.A.
3.
a) 8 - π
b) 8 - 2π
c) 8 + π
d) 16 - 4π
e) N.A.
4.
a) 4(4 - 2π - 2 3 )
b) 8(4 - 3
3
2
−
π
)
c) 16(4 - 3
3
2
−
π
)
COLEGIO “JOMAR”
A
O BO1
R=5
N
CA
P
30cm
B
30cm
30cm
A
D
B C

4. IIIB / MATEMÁTICA / 4º CLASES VIRTUALES
d) 16(2 - 3
3
−
π
)
e) N.A.
5.
a) 4π
b) 2π
χ) π
d) 8π
e) N.A.
6. En la figura. Calcular el área de la zona
sombreada.
a) 16π m
2
b) (8 + 4π)m
2
c) 8πm
2
d) 6πm
2
e) 16πm
2
7. Hallar el área del triángulo sombreado
contenido en el cuadrado de lado “L”.
a) L2
b) 3L2
/8
c) 5L2
/8
d) 3L2
/4
e) L2
/4
8. Hallar el área de la región sombreada si el lado
del cuadrado ABCD mide 4m.
a) 2πm
2
b) 4πm
2
c) 5πm
2
d) 3πm
2
e) 6πm
2
9. Si ABCD es un cuadrado de lado 4m. Calcular el
área de la región sombreada.
a) 6(2- 3 )m2
b) 2(4- 3 )m2
c) 9( 3 -1)m2
d) 4(2- 3 )m2
e) 8( 3 -1)m2
10. Siendo ABCD un cuadrado de lado 4m. Calcular
el área de la región sombreada.
a)
2
33448 π−−
b)
3
53848 π−−
c)
2
3848 π−−
d)
2
73648 π−−
e)
3
531248 π−−
11. En las siguientes figuras Ud. tiene que calcular
el área de la región sombreada si todos son
cuadrados de lado 4m.
a) 8m
2
b) 6m
2
c) 4m
2
d) 9m
2
e) 12m
2
12.
a) 4(6-π)m2
b) 16(6-π)m2
c) 16πm2
d) 24 - 2π
COLEGIO “JOMAR”
A B8m
A D
B C
D
CB
A
A
B C
D
A
D C
B

5. IIIB / MATEMÁTICA / 4º CLASES VIRTUALES
e) 4 2 m2
COLEGIO “JOMAR”

6. IIIB / MATEMÁTICA / 4º CLASES VIRTUALES
e) 4 2 m2
COLEGIO “JOMAR”