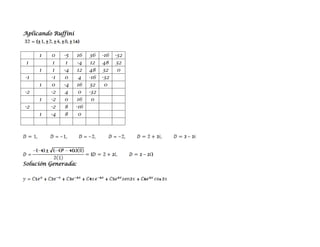
Este documento presenta una clase sobre ecuaciones diferenciales. Explica cómo determinar si una función es solución de una ecuación diferencial y resuelve varios tipos de ecuaciones diferenciales de primer y segundo orden usando métodos como integración, cambio de variable, factores integrantes y anuladores. El documento contiene ejemplos resueltos de cada tipo para ilustrar los conceptos y métodos.

1. UNIVERSIDAD FERMIN TORO
FACULTAD DE INGENERIA
ESCUELA DE TELECOMUNICACIONES
CABUDARE EDO-LARA
ECUACIONES DIFERENCIALES
MATEMATICA IV
Carlos Zerpa
CI: 17.455.469
Barquisimeto 17 marzo de 2012

2. Determine si la función es solución de la ecuación diferencial.
a)
Entonces:
, La función es solución de la ecuación diferencial
b)
Seguidamente:
La función es solución de la ecuación diferencial
c)

3. Entonces:
; Por consiguiente la función es solución de la ecuación diferencial.
2- Resolver las siguientes ecuaciones diferenciales de primer orden de acuerdo al método
correspondiente
A-

4. Al integrar resultaría
B-
Por lo tanto
Como entonces la ecuación diferencial es homogénea, con lo cual se puede
realizar un cambio de variable y=v.x de la siguiente forma:

5. Al integrar se obtiene:
Devolviendo el cambio de variable
Solución Generada:
C-
Verificando si es exacta:

6. Entonces la ecuación no es exacta, se verifica el factor integrante de la siguiente manera:
Entonces resulta:
Es el factor integrante, multipliquemos I por
, la cual de esta forma ahora debe ser exacta

7. La ecuación es exacta y se resuelve así de la siguiente manera
Así
D-
La ecuación posee una estructura de ecuación lineal de primer orden con lo que:
Por consiguiente la solución es de la siguiente forma:

8. Sustituyendo
3- Resolver las ecuaciones diferenciales de orden N según el método correspondiente:
A- (1)
Se usara el método de anuladores, entonces:
Anulador de R(x)
Entonces la ecuación (1) se puede escribir como:
(2)

9. Se multiplica en ambos lados de la igualdad A(D)
La solución tiene la siguiente forma:
Sustituyendo en (2) queda:
Desarrollando se tiene que:
Como la ecuación es demasiado larga la coloque en dos líneas profesor la cual es esta:
Sigue en la siguiente línea

10. Igualando coeficiente y simplificando:
La solución es:
B-
Es una ecuación homogénea la cual se escribe como:
Entonces
Polinomio característico

11. Aplicando Ruffini
1 0 -5 16 36 -16 -32
1 1 1 -4 12 48 32
1 1 -4 12 48 32 0
-1 -1 0 4 -16 -32
1 0 -4 16 32 0
-2 -2 4 0 -32
1 -2 0 16 0
-2 -2 8 -16
1 -4 8 0
Solución Generada: