Este documento presenta el modelo de flujo máximo para redes. Explica que las redes pueden tener capacidades unidireccionales o bidireccionales. Luego, formula matemáticamente el problema de flujo máximo y describe el algoritmo para encontrar el flujo máximo entre nodos origen y destino. Finalmente, incluye ejemplos y ejercicios para aplicar el modelo.

1. MODELO DE REDES
FRANCISCO VARGAS
INGENIERO DE SISTEMAS
ESPECIALISTA EN GERENCIA DE SISTEMAS INFORMÁTICOS
MAGÍSTER EN CIENCIAS DE LA INFORMACIÓN Y LAS COMUNICACIONES CON ÉNFASIS EN TELEINFORMÁTICA
CANDIDATO A DOCTOR EN CIENCIA Y TECNOLOGÍA INFORMÁTICA
2015

2. MODELO DE REDES
4. MODELO DEL FLUJO MÁXIMO
Rama (i,j) puede tener 2 capacidades distintas
Flujo de i a j Flujo de j a i
Ejp: Calle, línea telefónica, etc
(1 sentido y 2 sentidos)
0
1
2
3
4
5
6
7
8
9
Fuente Destino
Refinerías Estaciones de bombeo Terminales
Flujo en una sola dirección: 1,2,3, 7, ..
Flujo en cualquier dirección: 4,5,6

3. MODELO DE REDES
4.1 Formulación Matemática
1
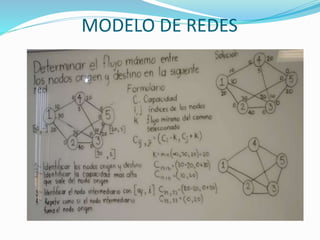
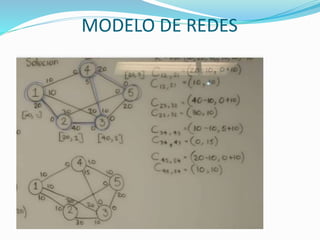
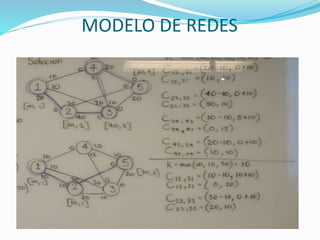
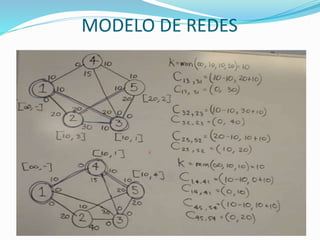
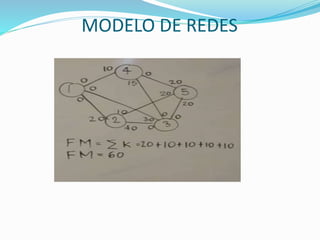
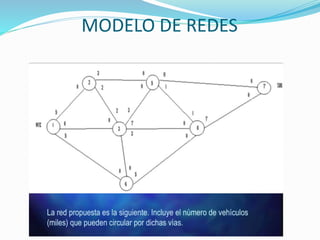
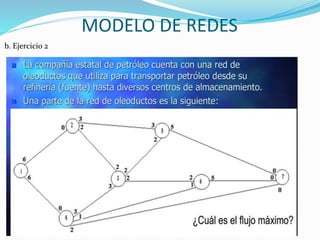
Determinar el flujo máximo entre los nodos origen y destino de la siguiente red:
4
2
5
3
20
30
10
0
5
20
0
0
0
20
10
0
0
40
30
0
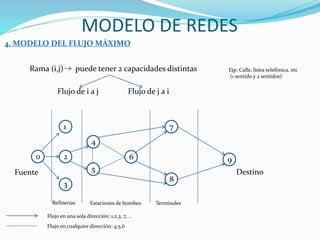
Notación:
C Capacidad
i,j índices de los nodos
k Flujo mínimo del camino seleccionado
C i,j , j,i =( C - k, C + k )i j
4.2 Algoritmo:
1. Identificar los nodos origen y destino
2. Identificar la capacidad más alta que sale del nodo origen
3. Identificar el nodo intermediario con [a , i]
4. Repetir como si el nodo intermediario fuera el nodo origen
a Cantidad de flujo máximo que recibe el nodo
i Nodo del que proviene el FM
f
FM = k
f

4. MODELO DE REDES
4.3 Ejemplo de Flujo Máximo

5. MODELO DE REDES

6. MODELO DE REDES

7. MODELO DE REDES

8. MODELO DE REDES

9. MODELO DE REDES

10. MODELO DE REDES
4.4 Ejercicios de Aplicación
a. Ejercicio 1:

11. MODELO DE REDES

12. MODELO DE REDES

13. MODELO DE REDES
b. Ejercicio 2

14. MODELO DE REDES

15. MODELO DE REDES