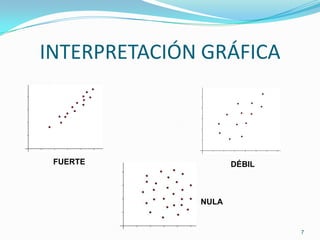
Este documento trata sobre la correlación lineal. Explica que la correlación mide la fuerza de la relación lineal entre dos variables usando un coeficiente de correlación entre -1 y 1. Un valor cercano a 1 indica una correlación positiva fuerte, mientras que cerca de -1 es una correlación negativa fuerte. También cubre cómo calcular la ecuación de la recta de regresión para estimar los valores de una variable basados en la otra.

1. REGRESIÓN LINEALUNIDAD 2: ESTADÍSTICA1

2. DISTRIBUCIONES BIDIMENSIONALESEn las distribuciones bidimensionales a cada individuo le corresponden los valores de dos variables que se representan por el par (xi , yi).2

3. DIAGRAMA DE DISPERSIÓNAl representar cada par de valores como las coordenadas de un punto, y se los grafica en un plano cartesiano, a este gráfico se le denomina diagrama de dispersión.3

4. COEFICIENTE DE CORRELACIÓNEl coeficiente de correlación es una medida de la fuerza de la relación lineal entre dos variables.En la fórmula anterior se tiene:COVARIANZA4

5. COEFICIENTE DE CORRELACIÓNEl coeficiente de correlación es un valor entre -1.0 y 1.0.Interpretación:5

6. INTERPRETACIÓN GRÁFICA6POSITIVANEGATIVA

7. INTERPRETACIÓN GRÁFICA7FUERTEDÉBILNULA

8. EJEMPLOUn estadista desea saber si existe una correlación entre los resultados de la prueba matemática del PSAT y los resultados en las pruebas de Estudios Matemáticos del IB. Para esto recolectó los datos de 10 estudiantes seleccionados al azar.8

9. CÁLCULO DEL COEFICIENTE DE CORRELACIÓN9

10. DIAGRAMA DE DISPERSIÓN EN CALCULADORA10

11. CÁLCULO DEL COEFICIENTE DE CORRELACIÓN11Como el valor del coeficiente de correlación (r) es 0.820 entonces se dice que existe una correlación positiva fuerte

12. RECTA DE REGRESIÓNLa recta de regresión se utiliza para estimar los valores de la variable y, a partir de los de la variable x.La ecuación de la recta de regresión esLa recta de regresión pasa por el punto 12

13. CÁLCULO DE LA ECUACIÓN DE LA RECTA DE REGRESIÓN13

14. EJERCICIOUn estudiante de Estudios Matemáticos recolectó datos para determinar si existe una correlación entre las edades de los estudiantes de colegio y las horas que destinan, semanalmente, a realizar sus tareas. El resultado de 10 estudiantes aleatorios se encuentran en la siguiente tabla:14

15. Realizar:A) Diagrama de dispersión (En hoja milimetrada).B) Cálculo de coeficiente de correlación.C) Análisis del coeficiente de correlación.D) Cálculo de la ecuación de la recta de regresión.E) Trazar la recta de regresión y ubicar el punto que contiene a las medias (En el mismo plano cartesiano del literal A).F) Realizar una estimación de la cantidad de horas que destina semanalmente, un estudiante de 15 años.15