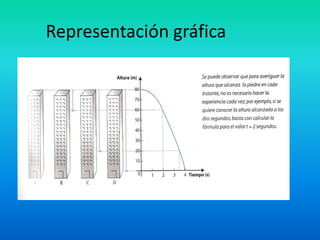
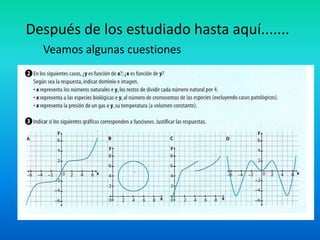
Este documento presenta conceptos clave sobre funciones, incluyendo: 1) Las funciones mapean elementos de un conjunto dominio a elementos de un conjunto codominio siguiendo una regla; 2) Ejemplos de funciones incluyen la altura de una piedra al caer, dada por la fórmula h(t)=80-5t^2; 3) El dominio es el conjunto de valores posibles de la variable independiente y el codominio es el conjunto de valores posibles de la variable dependiente.

1. INFORMATICA EDUCATIVA
PLAN DE CLASE
ALUMNO: LEONARDO LÓPEZ

2. TIPOS DE RELACIONES
Las relaciones definidas en un conjunto
pueden cumplir o no las propiedades ya
descriptas, expuestas en clases anteriores
Las relaciones más usuales en matemática
son:
Las relaciones de equivalencia
Las relaciones de orden
Las relaciones funcionales o
aplicaciones.

3. Relaciones funcionales
Definición:
Una relación f entre elementos de un conjunto A y
elementos de un conjunto B es una función o
aplicación de A en B si y sólo si, verifica las siguientes
condiciones:
1º) Condición de Existencia:
x A, y B / (x ; y) f
2º)Condición de Unicidad:
(x ; y) f (x ; z) f y=z

4. Ejemplo
Una fábrica de impresoras quiere lanzar al mercado
un nuevo modelo. Para ello realiza un estudio y se
determina que la ganancia ( en miles pesos) está
dada por el precio de venta (en pesos)
esta relación viene establecida por la siguiente
fórmula: g(p) = -4 ( p – 250) + 10000, donde “p”
representa el precio de venta.
a) ¿ A qué precio conviene vender las impresoras
para obtener la máxima ganancia?
b) ¿Existe algún precio para el cual no hay ganancia

5. Las Funciones
Las funciones son una herramienta útil para
describir, analizar e interpretar situaciones
provenientes de la Matemática misma y de otras
ciencias
Planteamientos al abordar las funciones
Las preguntas que podríamos hacernos al
abordar este concepto podrían ser, entre
otras, las siguientes:

6. ¿Qué tipos de funciones son las
que necesitamos conocer?

7. ¿Para qué valores de la variable
independiente resulta que la
variable dependiente va creciendo
o decreciendo...?

8. ¿Cómo es el crecimiento de la
función rápido, lento, ...?
¿Cómo medir el crecimiento’

9. ¿ Qué representación se les
puede dar para hacernos
una mejor idea de sus
características y de su
significado?

10. Veamos algunos casos
Y sus diferentes representaciones

11. Representación Verbal
---“Se deja caer una piedra desde el techo de un
edificio que mide 80 m de altura y se quiere
describir còmo varìa la altura de la piedra en
relación con el tiempo, es decir, desde que comienza
a caer hasta que toca el suelo.”
--Como en cada instante t la piedra se encuentra a
una ùnica altura h del suelo, se dice que la relación
entre h y t es una función, o que h es fucnión de t.

12. Representación algebraica
La física ha adoptado de la matemática un modelo
que se adapte para describir la caída libre de los
cuerpos a través de la fórmula:
h(t) = h0 + v0 . t – ½ g t2
Donde h0 y v0 son parámetros: el primero
representa la altura desde donde es lanzado un
cuerpo, y el segundo, la velocidad con la que el
cuerpo es arrojado; g es una constante que
representa la aceleración de la gravedad

13. Representación gráfica

14. Representación algorítmica
Se trata, entonces, de encontrar una
fórmula que permita calcular para cada
valor de t, el único valor de h que le
corresponde.
Si h0 = 80m ; v0 = 0, porque la piedra se
deja caer a partir del reposo, y ½ . g 5
la expresión algebraica buscada
será:
h(t) = 80 – 5 . t2

15. Relaciones entre variables
Para describir una relación entre dos
variables x e y, utilizando una función, es
necesario encontrar una ley que asigne a
cada valor de x ( variable independiente), un
único valor de y (variable dependiente).
En la situación de caída libre -de la piedra- t
es la variable independiente, h es la variable
dependiente, y la fórmula h(t) = 80 – 5t2 es
la ley o propiedad que asigna a cada valor de
t un único valor de h.

16. Más definiciones
Una función f queda determinada por:
Un conjunto A llamado dominio.
Un conjunto B llamado codominio.
Una ley que asocia a cada elemento x del
conjunto A un único elemento de B.
Veamos esto gráficamente:

17. Dominio y Codominio

18. Análisis de los conceptos
Esta definición incluye conjuntos de elementos
cualesquiera, numéricos o no numéricos, y
abarca tanto la ley de correspondencia como los
conjuntos en los que toman sus valores las
variables.
De acuerdo con esta definición, dos funciones
son iguales si coinciden su dominio, su
codominio y la ley de correspondencia que
relaciona los elementos de ambos conjuntos

19. El Dominio
El dominio de una función es el conjunto
formado por todos los valores que toma la
variable independiente x y se simboliza
Dom(f)
En la situación 1, de la piedra, el dominio
de la función es el intervalo 0 ; 4

20. El Codominio
El codominio de una función f es un
conjunto que contiene a todos los
valores que puede tomar la función.
Las funciones estudiadas, en este curso,
tendrán como dominio al conjunto de
los números R o a un subconjunto del
mismo, y como codominio igual a R.

21. Imagen de una función
Cada elemento y está asociado a un elemento x del
dominio de f, se llama imagen de x y se escribe f(x) (se
lee “efe de x”).
En la situación 1, el valor h = 0 está asociado a t = 4, que
es un elemento perteneciente al dominio de la función;
0 es la imagen de 4 y se escribe h(4).
El conjunto formado por todas las imágenes de los
elementos del dominio de f se llama imagen de f y se
simboliza Im(f). observemos que la imagen está
contenida en el codominio.
En la situación 1, la imagen de la función es el intervalo
0 ; 80

22. Después de los estudiado hasta aquí.......
Veamos algunas cuestiones