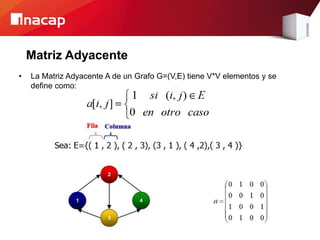
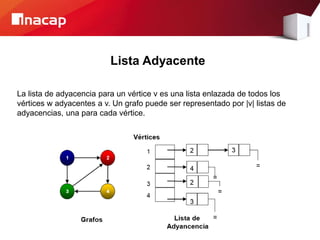
Este documento describe dos métodos para representar grafos: la matriz de adyacencia y la lista de adyacencia. La matriz de adyacencia almacena la información de conectividad en una tabla donde cada fila y columna representa un vértice, mientras que la lista de adyacencia almacena las conexiones de cada vértice en una lista enlazada. El documento analiza las ventajas y desventajas de ambos métodos, como que la matriz requiere más espacio pero permite verificar conexiones más rápido, mientras que la lista usa

1. Representación de los Grafos
Alumno: Pedro Avaria
Docente: Pilar Pardo

2. Representación de los grafos
Un grafo Dirigido o No-Dirigido se puede representar mediante:
• Matriz de Adyacencia
• Lista de Adyacencia
• Arreglos para la Lista de Adyacencia.
Sea el siguiente Grafo Dirigido:
Donde:
V={1,2,3,4}
E={(1,2),(2,3), (,3,1), ((4,2),(3,4)}

3. Matriz Adyacente
• La Matriz Adyacente A de un Grafo G=(V,E) tiene V*V elementos y se
define como:

4. Ventajas y Desventajas de la Matriz Adyacente
VENTAJAS:
• Se puede determinar en un
tiempo fijo y constante si un
enlace(arco) pertenece o no al
grafo.
• Es fácil determinar si existe o
no un arco o enlace, solo se
debe posicionar en la matriz.
• Es fácil determinar si existe un
ciclo en el grafo, basta
multiplicar la matriz por ella
misma n veces hasta obtener
la matriz nula(no hay ciclos) o
bien una sucesión periódica
de matrices(hay ciclo)
DESVENTAJAS:
• Se requiere un almacenamiento |v|*|v|.
Es decir O(n2).
• Solo al leer o examinar la matriz puede
llevar un tiempo

5. Lista Adyacente
La lista de adyacencia para un vértice v es una lista enlazada de todos los
vértices w adyacentes a v. Un grafo puede ser representado por |v| listas de
adyacencias, una para cada vértice.

6. Ventajas:
• La lista de adyacencia requiere un
espacio proporcional a la suma
del número de vértices más el
número de enlaces(arcos). Hace
buen uso de la memoria.
• Se utiliza bastante cuando el
número de enlaces es mucho
menor que O(n2)
Ventajas y Desventajas de la Lista Adyacente
Desventajas:
• La representación con lista de
adyacencia es que puede llevar
un tiempo O(n) determinar si
existe un arco del vértice i al
vértice j, ya que pueden haber
O(n) vértices en la lista de
adyacencia. Para el vértice i.

7. Arreglos para la Lista de Adyacencia.
• Se utilizan los arreglos para implementar la Lista de Adyacencia: