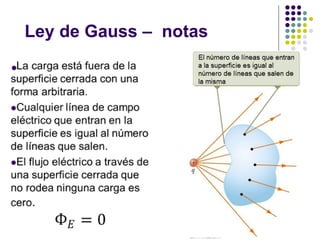
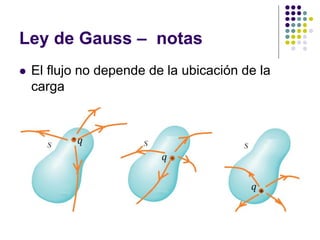
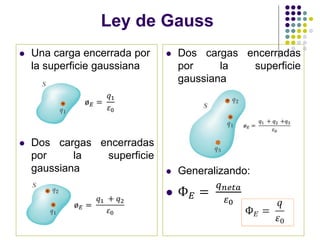
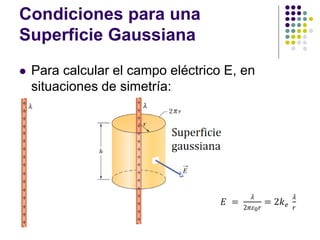
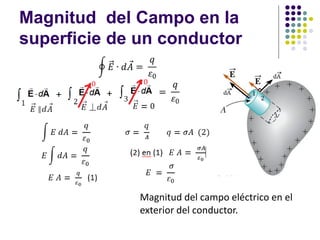
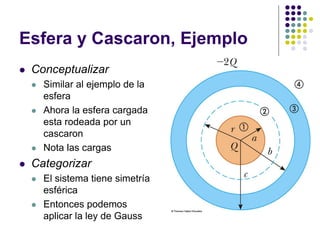
El documento aborda la ley de Gauss, enfatizando su aplicación para calcular el campo eléctrico de distribuciones de carga simétricas. Se discuten conceptos fundamentales como el flujo eléctrico y las propiedades de los conductores en equilibrio electrostático. Se incluyen ejemplos y ejercicios para ilustrar la utilización de la ley de Gauss en la resolución de problemas de alta simetría.

1. Frase del día
“El genio
es 1% de talento y
99% de trabajo
duro”
Albert Einstein

2. Capitulo 2
La Ley de Gauss
Mg. Felícitas Nina Herrera

3. Ley de Gauss
Competencia
Determinar la carga eléctrica y el campo
eléctrico utilizando la ley de Gauss para
resolver problemas de alta simetría, con una
actitud crítica y responsable.

4. Ley de Gauss
Contenido:
⚫ Flujo eléctrico
⚫ Ley de Gauss
⚫ Aplicaciones de la ley de Gauss a varias
distribuciones de carga
⚫ Conductores en equilibrio electrostático
⚫ Ejercicios y problemas de aplicación.

5. PREGUNTA DE INICIO DE CAPÍTULO
¡Adivine ahora!
Una esfera aislante tiene una densidad de carga
uniforme distribuida sobre toda su superficie.
¿Cómo varía la magnitud del campo eléctrico en
el interior con la distancia desde el centro?

6. PREGUNTA DE INICIO DE CAPÍTULO
¡Adivine ahora!
a. El campo eléctrico es cero en todas partes.
b. El campo eléctrico es constante, pero distinto de
cero en todas partes.
c. El campo eléctrico se incrementa linealmente
con la distancia desde el centro hacia fuera.
d. El campo eléctrico se incrementa
exponencialmente con la distancia desde el
centro hacia fuera.
e. El campo eléctrico se incrementa
cuadráticamente con la distancia desde el centro
hacia fuera.

7. Introducción
⚫ El flujo es un concepto general y ampliamente aplicable
en física. Sin embargo, en este capítulo, nos
concentraremos en el flujo del campo eléctrico. Esto nos
permite introducir la ley de Gauss, que es particularmente
útil para encontrar los campos eléctricos de las
distribuciones de carga que exhiben simetría espacial. Los
principales temas discutidos aquí son
1. Flujo eléctrico. Definimos flujo eléctrico para superficies
abiertas y cerradas.
2. La ley de Gauss. Derivamos la ley de Gauss para una
distribución de carga arbitraria y examinamos el papel del
flujo eléctrico en la ley de Gauss.

8. Introducción
3. Cálculo de campos eléctricos con la ley de Gauss. El enfoque
principal de este capítulo es explicar cómo usar la ley de Gauss para
encontrar los campos eléctricos de distribuciones de carga
espacialmente simétricas. Discutiremos la importancia de elegir una
superficie Gaussiana y proporcionaremos ejemplos que involucran
las aplicaciones de la ley de Gauss.
4. Campos eléctricos en conductores. La ley de Gauss proporciona
información útil sobre la ausencia de campos eléctricos en los
materiales conductores.
⚫ Sin embargo, hay una trampa: la ley de Gauss tiene una limitación
porque, aunque siempre es cierta, puede aplicarse fácilmente solo
para distribuciones de carga con ciertas simetrías.

9. Introducción
⚫ El campo eléctrico producido por objetos cargados
estáticos se puede calcular mediante dos procedimientos
equivalentes: la Ley de Coulomb y la ley de Gauss.
⚫ En el capítulo anterior se describió el primer
procedimiento, en éste se presentará el segundo.
⚫ La Ley de Coulomb es una forma simple y directa de
expresar la fuerza eléctrica, mientras que la ley de Gauss
es más sutil, más compleja y, a veces, más útil.
⚫ La ley de Gauss requiere una complejidad matemática
mayor que la ley de Coulumb, con su uso adquiere un
conocimiento más profundo de la interacción eléctrica.

10. Flujo Eléctrico
El número de líneas de
campo eléctrico que
atraviesa una superficie
llama flujo eléctrico.
El concepto de flujo describe cuánto de algo pasa por un área
determinada. Más formalmente, es el producto escalar de un
campo vectorial (el campo eléctrico) con un área. Puedes
conceptualizar el flujo de un campo eléctrico como una medida
del número de líneas de campo eléctrico que pasan a través de
un área (Figura 6.3). Cuanto más grande es el área, más líneas de
campo pasan por ella y, por lo tanto, mayor es el flujo; de manera
similar, cuanto más fuerte es el campo eléctrico (representado por
una mayor densidad de líneas), mayor es el flujo.

11. Flujo Eléctrico
⚫ El Flujo Eléctrico es
el producto de la
magnitud del campo
eléctrico y el área de
superficie, A,
perpendicular al
campo eléctrico
⚫ ΦE = EA

12. Flujo Eléctrico, Área General
⚫ El flujo eléctrico es
proporcional al numero
de líneas de campo
que atraviesan alguna
superficie
⚫ Las líneas de campo
pueden formar cierto
ángulo θ con la
perpendicular a la
superficie
⚫ Entonces:
ΦE = EA cos θ

13. Flujo Eléctrico, Interpretación
de la Ecuación
⚫

14. Flujo Eléctrico, Interpretación
de la Ecuación
⚫

15. Flujo Eléctrico, Interpretación
de la Ecuación
⚫

16. Flujo Eléctrico, Interpretación
de la Ecuación
⚫

17. Flujo Eléctrico, General
⚫

18. Flujo Eléctrico, final
⚫

19. Flujo Eléctrico, Superficie
Cerrada
⚫ Consideremos una
superficie cerrada
⚫ Los vectores en
cada punto tiene
diferentes direcciones
⚫ En cada punto, es
perpendicular al
elemento de superficie
⚫ Por convención, apuntan
hacia afuera
i
A

20. Flujo a Través de una Superficie
Cerrada, continuación.
⚫

21. Flujo a Través de una
Superficie Cerrada, final
⚫

22. Ejemplo, Flujo a Través de un
Cubo
⚫

23. Karl Friedrich Gauss
⚫ 1777 – 1855
⚫ Karl Friedrich Gauss (1777-1855) fue un fabuloso
matemático del siglo XIX. Aunque sus principales
contribuciones fueron al campo de las matemáticas,
también hizo un trabajo importante en física y
astronomía.
⚫ Esta ley se llama en honor al extraordinario
matemático y científico alemán Karl Friedrich Gauss .
La ley de Gauss nos brinda una forma elegantemente
simple de encontrar el campo eléctrico y, como verás,
puede ser mucho más fácil de usar que el método de
integración descrito en el capítulo anterior. Sin
embargo, hay una trampa: la ley de Gauss tiene una
limitación porque, aunque siempre es cierta, puede
aplicarse fácilmente solo para distribuciones de carga
con ciertas simetrías.

24. Ley de Gauss, Introducción
⚫ La ley de Gauss es una expresión general
entre el flujo eléctrico neto o total a través de
una superficie cerrada y la carga encerrada
por la superficie
⚫ La superficie cerrada a menudo se le llama
superficie gaussiana
⚫ La ley de Gauss es fundamental en el
estudio de los campos eléctricos

25. Ley de Gauss – General
⚫

26. Ley de Gauss – General
Enunciado de la ley de Gauss:
“ El flujo eléctrico a través de una superficie cerrada arbitraria
es igual a la carga neta encerrada por la superficie dividida
entre 𝜀0”
En forma de ecuación:
Ф𝐸 =
σ 𝑞
𝜀0
𝑜 ර 𝐸 ∙ 𝑑 Ԧ
𝐴 =
σ 𝑞
𝜀0
donde la superficie cerrada (superficie gaussiana) para que
se calcula el flujo debe tener cualquier forma y tamaño, el
signo σ 𝑞 representa la carga neta contenida en el volumen
que cierra la superficie.

27. Ley de Gauss – General
Como primer ejemplo de la ley de Gauss, suponga que la
expresión del campo eléctrico producido por una carga
puntual no se conoce, y para determinar se utiliza la ley de
Gauss.
En la figura se muestra una superficie gaussiana esférica
de radio 𝑟 con una carga puntual 𝑞 en su centro.

28. Ley de Gauss – General

29. Ley de Gauss – General

30. Ley de Gauss – general
⚫

31. Ley de Gauss – Nota
⚫

32. Ley de Gauss – notas

33. Ley de Gauss – notas

34. Ley de Gauss – notas
⚫ El flujo no depende de la ubicación de la
carga

35. Ley de Gauss
⚫ Una carga encerrada por
la superficie gaussiana
⚫ Dos cargas encerradas
por la superficie
gaussiana
⚫ Dos cargas encerradas
por la superficie
gaussiana
⚫ Generalizando:
⚫ Ф𝐸 =
𝑞𝑛𝑒𝑡𝑎
𝜀0

36. Ley de Gauss – notas
⚫ El flujo neto a través de cualquier superficie cerrada que
rodea una carga puntual, q, esta dada por q/εo y es
independiente de la forma de esa superficie
⚫ El flujo eléctrico neto a través de una superficie que NO
rodea ninguna carga es CERO
⚫ Dado que el campo eléctrico debido a muchas cargas es la
suma vectorial de los campos eléctricos producidos por las
cargas individuales, el flujo a través de cualquier superficie
cerrada se puede expresar como:

37. Ley de Gauss – Final
⚫

38. Ley de Gauss - Final
⚫

39. Aplicaciones de la Ley de Gauss
⚫ Para usar la ley de Gauss, desea elegir una
superficie gaussiana sobre la cual se pueda
simplificar la integral de la superficie y
determinar el campo eléctrico
⚫ Aproveche la simetría
⚫ Recuerde, la superficie gaussiana que usted
elija, no tiene que coincidir con una superficie
real

40. Aplicaciones de la Ley de Gauss
⚫

41. Condiciones para una
Superficie Gaussiana
⚫ Elija una superficie gaussiana que satisfaga las
siguientes condiciones:
⚫ El valor del campo eléctrico puede mostrarse desde la
simetría como constante sobre la superficie gaussiana
⚫ El producto punto se puede expresar en un simple
producto EdA debido a que y son paralelos
⚫ El producto punto es cero debido a qu se y son
perpendiculares
⚫ El campo es cero sobre la porción de la superficie
E
d

E A
E dA
dA

42. Condiciones para una
Superficie Gaussiana
⚫ Para calcular el campo eléctrico E, en
situaciones de simetría:

43. Campo debido a una línea de
Carga, continuación.
⚫

44. Condiciones para una
Superficie Gaussiana
⚫

45. Condiciones para una
Superficie Gaussiana
⚫

46. Ahora te toca estudiar, próxima clase
problemas de aplicación

47. Equilibrio Electrostático (Conductores)
⚫

48. Propiedades de un Conductor
en Equilibrio Electrostático
⚫

49. Propiedades de un Conductor
en Equilibrio Electrostático
⚫

50. Propiedades de un Conductor
en Equilibrio Electrostático
Conductor de cualquier
forma cargado ⚫

51. Propiedades de un Conductor
en Equilibrio Electrostático
⚫ En un conductor de forma irregular, la densidad de carga
superficial es mayor en lugares donde el radio de
curvatura es el más pequeño

52. Propiedad 1: Campo Edentro = 0,
continuation
⚫ Un buen conductor contiene cargas (electrones)
que no se encuentran unidas a ningún átomo y
debido por ello los electrones tienen la libertad
de moverse en el interior del material.
⚫ Dentro de un conductor no existe ningún
movimiento neto de carga, el conductor está en
equilibrio electrostático.
⚫ Hay un campo neto de CERO dentro del conductor
⚫ Esta redistribución dura alrededor de 10-16s y
podemos considerarla como instantánea

53. Propiedad 2: Carga Reside en
la Superficie
⚫ Elegimos una superficie
gaussiana dentro del
conductor pero cerca de la
superficie real
⚫ El campo eléctrico dentro del
conductor es CERO
⚫ No hay flujo neto a través de
la superficie gaussiana
⚫ Debido a que la superficie
gaussiana puede estar tan
cerca de la superficie real
como se desee, no puede
haber carga dentro de la
superficie

54. Propiedad 2: Carga Reside en
la Superficie, continuation
⚫ Como no puede haber carga neta dentro de
la superficie, cualquier carga neta deberá
residir en la superficie
⚫ La ley de Gauss no indica la distribución de
estas cargas, solo que debe estar en la
superficie del conductor

55. Propiedad 3: Magnitud y
Dirección del Campo
⚫

56. Magnitud del Campo en la
superficie de un conductor
Magnitud del campo eléctrico en el
exterior del conductor.

57. Propiedad 3: Magnitud y Dirección
del Campo, continuación.
⚫ El flujo neto a través de la superficie
gaussiana es solo a través de la cara plana
fuera del conductor
⚫ El campo aquí es perpendicular a la superficie
⚫ Aplicando la ley de Gauss
E
o o
σA σ
EA and E
ε ε
 = = =

58. Esfera y Cascaron, Ejemplo
⚫ Conceptualizar
⚫ Similar al ejemplo de la
esfera
⚫ Ahora la esfera cargada
esta rodeada por un
cascaron
⚫ Nota las cargas
⚫ Categorizar
⚫ El sistema tiene simetría
esférica
⚫ Entonces podemos
aplicar la ley de Gauss

59. Esfera y Cascaron, Ejemplo 2
⚫ Analizar
⚫ Considere una esfera gaussiana entre la
superficie de la esfera sólida y la superficie
interna del cascaron
⚫ Las líneas del campo eléctrico deben dirigirse
radialmente hacia afuera y el campo eléctrico
debe tener una magnitud constante en la
superficie gaussiana.

60. Esfera y Cascaron, Ejemplo 3
⚫ Analizar, continuación
⚫ Se puede calcular el campo para cada caso
1 3
2 2
3
4 2
( )
( )
0 ( )
( )
e
e
e
Q
E k r for r a
a
Q
E k for a r b
r
E for b r c
Q
E k for r c
r
= 
=  
=  
= − 

61. Esfera y Cascaron, Ejemplo
final
⚫ Finalizar
⚫ Verifique la carga neta
⚫ Piense en otras combinaciones posibles
⚫ Pregúntese por ejemplo
⚫ ¿Qué pasaría si la esfera en lugar de conductor es
un aislante?

62. Ahora te toca estudiar, próxima clase
problemas de aplicación

63. Ahora te toca estudiar