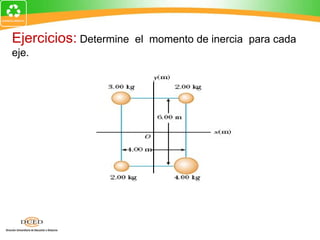
El documento resume conceptos clave de dinámica rotacional como energía cinética de rotación, inercia rotacional, momento de inercia, teorema de ejes paralelos, momento angular y su conservación. Proporciona ejemplos y ejercicios para calcular el momento de inercia de diferentes objetos como partículas, barras, discos y esferas.

1. Lic. Fis. Carlos Levano Huamaccto CICLO 2011-I Módulo: Unidad: 7 Semana: 7 FISICA I

2. DINAMICA ROTACIONAL

3. Energía Cinética de Rotación Inercia de Rotacional Momento de Inercia Teorema de ejes paralelos Momento Angular Conservación del Momento Angular CONTENIDOS TEMÁTICOS

4. ENERGÍA CINÉTICA DE ROTACIÓN

5. Es la energía de movimiento rotacional .

6. Ejemplos K=(1/2)(2Kgm 2 )( 2 rad/s) 2 = 4J I=(2Kg)(1m) 2 =2 Kgm 2

7. INERCIA ROTACIONAL Es la resistencia de un objeto a los cambios en su movimiento de rotaci ón, es decir, los objetos en rotación tienden a permanecer en este estado, mientras que los objetos que no giran tienden a permanecer sin girar.

8. Si la mayor ía de la masa está ubicada muy lejos del centro de rotación, la inercia de rotación será muy alta y costará hacerlo girar o detener su rotación.

9. Si la masa est á cerca del centro de rotación de un determinado objeto, la inercia será menor y será más fácil hacerlo girar. Eje de giro

10. MOMENTO DE INERCIA Es la medida de la inercia rotacional . Discreto Continuo

11. EJEMPLOS: Momento de inercia de cuatro cuerpos puntuales.

12. EJEMPLOS: Determinar el momento de inercia del sistema de cuatro partículas puntuales.

13. Ejercicios: Determine el momento de inercia para cada eje.

14. EJEMPLO: Momento de Inercia de una barrra

15. Ejemplo: Determinar el momento de inercia del sistema

16. M0MENTO DE INERCIA DE ALGUNOS CUERPOS

17. TEOREMA DE EJES PARALELOS

18. TORQUE Y MOMENTO ANGULAR Recuerden

19. Relación entre torque y aceleración angular Partícula

20. Cuerpo

21. EJEMPLOS: Determinar la aceleración tangencial Determine la aceleración angular de la rueda. Solución:

23. MOMENTUM ANGULAR

24. MOMENTO ANGULAR El momento angular o cantidad de movimiento angular es una magnitud que resulta del producto entre el momento de inercia(I) y la velocidad angular (  ) de un cuerpo en rotación. Es un vector que se determina con la regla de la mano derecha y su módulo es L = I · ω Sus unidades Sistema Internacional: kg·m ² /s CGS: g·cm ² /s

25. Momento Angular (L) Se relaciona con el hecho de que un objeto en rotaci ón persiste en este tipo de movimiento. El momento angular produce una cierta estabilidad de giro en el eje de rotación. Por eso es fácil mantener el equilibrio en una bicicleta en movimiento, ya que al girar las ruedas se produce este fenómeno.

26. Conservaci ón del momento angular Cuando un cuerpo se encuentra girando , su momento angular permanece constante a no ser que sobre él actúe un torque externo que lo haga modificar su estado de rotación. Luego si el torque externo es cero, el momento angular final (Lf)Es igual al momento angular inicial(Li). I inicial · ω inicial = I final · ω final

27. Ejemplo.- Una rueda de bicicleta girando horizontalmente experimenta una variación en su velocidad angular. Esto significa que pudo variar. I. su inercia rotacional. II. su momento angular. III. el torque neto sobre ella. Es o son verdadera(s): A) sólo I B) sólo II C) sólo III D) sólo I y II E) sólo II y III

28. Ejemplo: Calcular el momento de inercia de disco

29. Ejemplo.- Calcular el momento de inercia de un rectángulo homogéneo cuyas dimensiones son a  b , su densidad superficial es  y su espesor despreciable, respecto a los ejes X, Y, Z indicados en la figura. solución a b La masa de la figura es su área por su densidad superficial Momento de inercia respecto al eje X X Y Z En función de la masa M

30. Primero consideremos el momento de inercia respecto al centro O Por lo tanto, para una figura plana Usando los resultados anteriores figura plana

31. Ejemplo:- Calcular el momento de inercia de una esfera homogénea de radio R y densidad  respecto a uno de sus diámetros. O Ya que todos los puntos materiales de cada una de esas capas está situado a la misma distancia r del centro, el momento de inercia respecto de O es:

32. GRACIAS