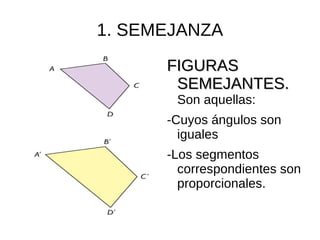
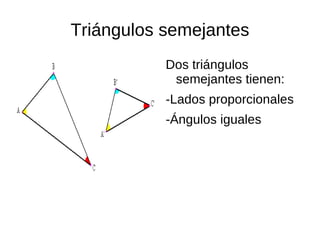
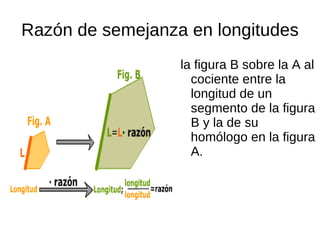
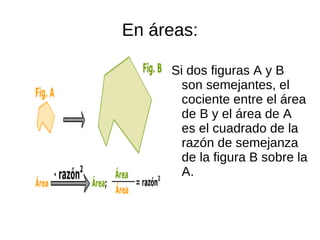
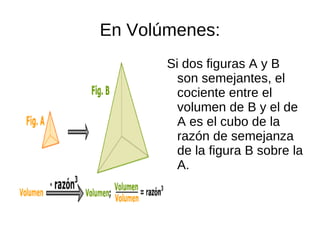
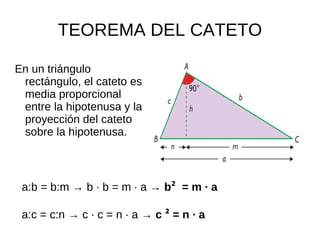
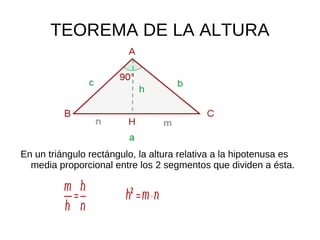
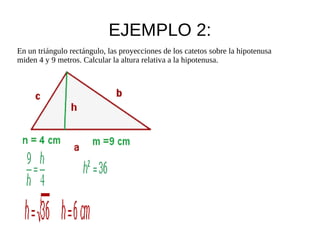
El documento describe la semejanza de figuras geométricas y sus aplicaciones. Las figuras semejantes tienen ángulos iguales y lados proporcionales. Las aplicaciones incluyen escalas, donde la razón entre las longitudes de una reproducción y la realidad da la escala, y cómo la semejanza afecta áreas y volúmenes. También presenta teoremas sobre triángulos rectángulos, incluyendo el teorema del cateto y el de la altura.

1. LA SEMEJANZA Y
SUS APLICACIONES

2. 1. SEMEJANZA
FIGURAS
SEMEJANTES.
Son aquellas:
-Cuyos ángulos son
iguales
-Los segmentos
correspondientes son
proporcionales.

3. Teorema de Tales
Si varias rectas
paralelas (a, b, c)
cortan a dos rectas
cualesquiera, los
segmentos que
determinan en ellas
son proporcionales

4. Triángulos semejantes
Dos triángulos
semejantes tienen:
-Lados proporcionales
-Ángulos iguales

5. 6.APLICACIONES
ESCALAS. Es el
cociente entre cada
longitud de la
reproducción y la
correspondiente
longitud en la
realidad.
Mapa topográfico con escala de Es la razón de
reducción 1:250.000, lo que significa
que cada centímetro en el mapa son semejanza entre la
2,5 kilómetros en la realidad. reproducción y la
realidad.

6. Razón de semejanza en longitudes
la figura B sobre la A al
cociente entre la
longitud de un
segmento de la figura
B y la de su
homólogo en la figura
A.

7. En áreas:
Si dos figuras A y B
son semejantes, el
cociente entre el área
de B y el área de A
es el cuadrado de la
razón de semejanza
de la figura B sobre la
A.

8. En Volúmenes:
Si dos figuras A y B
son semejantes, el
cociente entre el
volumen de B y el de
A es el cubo de la
razón de semejanza
de la figura B sobre la
A.

9. TEOREMA DEL CATETO
En un triángulo
rectángulo, el cateto es
media proporcional
entre la hipotenusa y la
proyección del cateto
sobre la hipotenusa.
a:b = b:m → b · b = m · a → b² = m · a
a:c = c:n → c · c = n · a → c ² = n · a

10. EJEMPLO 1:
La hipotenusa de un
triángulo rectángulo
mide 30 cm y la
proyección de un
cateto sobre ella
10.8 cm. Hallar el

11. TEOREMA DE LA ALTURA
En un triángulo rectángulo, la altura relativa a la hipotenusa es
media proporcional entre los 2 segmentos que dividen a ésta.

12. EJEMPLO 1:
Tenemos un triángulo rectángulo, de forma que la altura relativa a la hipotenusa determina sobre ésta, dos
segmentos de longitudes 1,8 cm y 3,2 cm. Halla:
a) La longitud de la altura correspondiente a la hipotenusa.
b) La longitud de los catetos.
c) El área del triángulo. Datos:
n=1,8 cm
m=3,2 cm
¿h?
¿a?
a) Usamos el Teorema de la altura: h² =n·m
h²=1,8·3,2 h=2,4cm
b) El valor de la hipotenusa sería: a=m+n
a= 1,8+3,2 a=5cm
c) Área= (base·altura):2=(5·2,4):2=12:2=6cm²

13. EJEMPLO 2:
En un triángulo rectángulo, las proyecciones de los catetos sobre la hipotenusa
miden 4 y 9 metros. Calcular la altura relativa a la hipotenusa.

14. TEOREMA DE PITÁGORAS
GENERALIZADO